数学沪科版第14章 全等三角形14.2 三角形全等的判定教课课件ppt

这是一份数学沪科版第14章 全等三角形14.2 三角形全等的判定教课课件ppt，共18页。PPT课件主要包含了△ABC即为所求，它们是全等的，已知△ABC，几何语言，∠B∠B，BCBC，∠C∠C，AAAS，BASA，CSAS等内容，欢迎下载使用。

准备好了吗？一起去探索吧！
1.理解并掌握判定两个三角形全等“角边角”判定定理.2.在探究“角边角”判定定理的过程中，能进行有条理的思考.3.通过学习以上内容，培养严谨的分析能力，体会几何学的应用价值．4.通过探究对给定的两角及夹边来确定三角形的形状和大小是否唯一这一过程，培养学生分析问题、解决问题的能力.
三角形全等的判定-ASA
到目前为止，可以作为判定两个三角形全等的方法有几种？
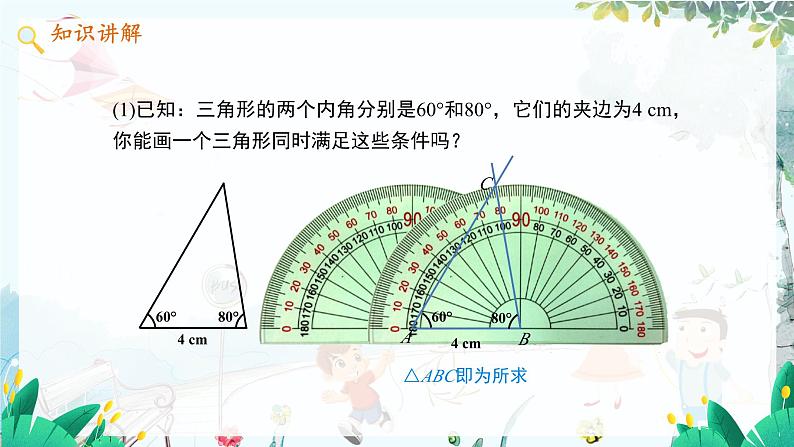
(1)已知：三角形的两个内角分别是60°和80°，它们的夹边为4 cm，你能画一个三角形同时满足这些条件吗？
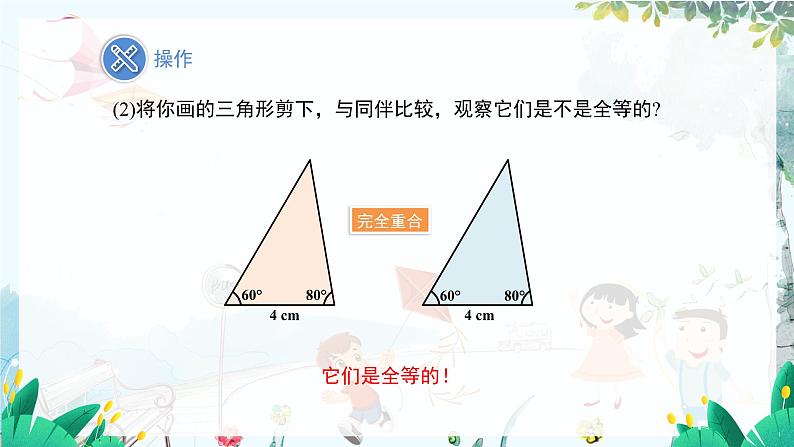
(2)将你画的三角形剪下，与同伴比较，观察它们是不是全等的?
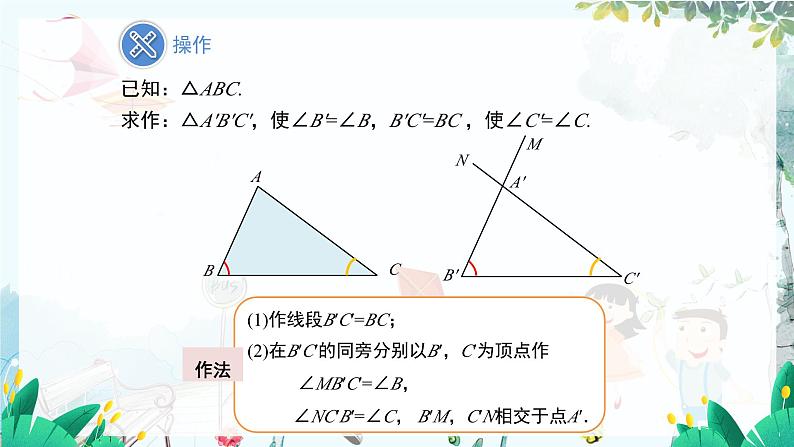
求作：△A'B'C'，使∠B'=∠B，B'C'=BC ，使∠C'=∠C.
(1)作线段B′C′=BC；
(2)在B′C′的同旁分别以B′，C′为顶点作 ∠MB′C′=∠B， ∠NC′B′=∠C， B′M，C′N相交于点A′．
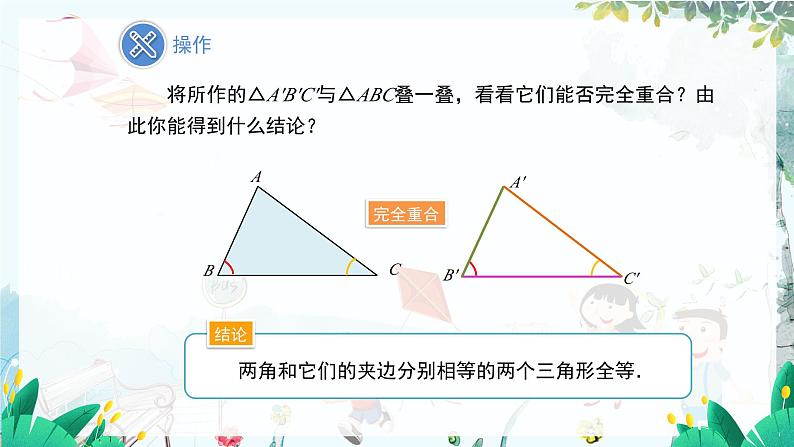
将所作的△A'B'C'与△ABC叠一叠，看看它们能否完全重合？由此你能得到什么结论？
两角和它们的夹边分别相等的两个三角形全等．
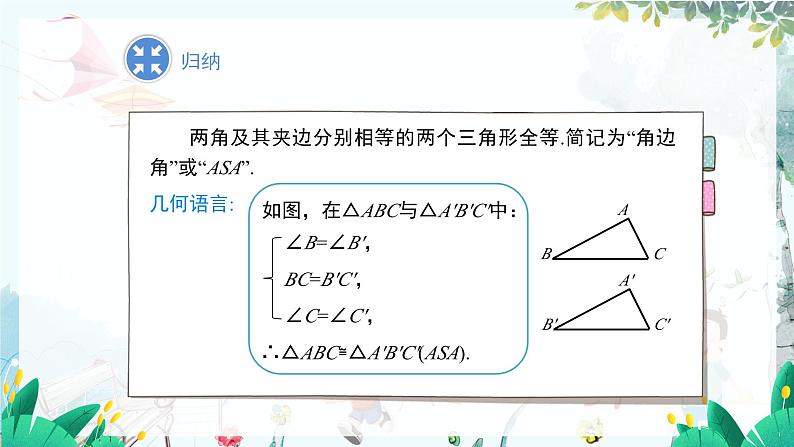
两角及其夹边分别相等的两个三角形全等.简记为“角边角”或“ASA”.
如图，在△ABC与△A'B'C'中：
∴△ABC≌△A'B'C'(ASA).
例1 已知：如图，∠1=∠2，∠3=∠4.求证：DB=CB.
分析：BD和CB分别在△ABD和△ABC中，所以要证BD=CB，只需证明△ABD≌△ABC即可.已知： ∠1=∠2，由∠3=∠4，可得∠ABD=∠ABC，AB是两个三角形的公共边.
证明：∵∠ABD与∠3互为邻补角， ∠ABC与∠4互为邻补角，(已知)又 ∵∠3=∠4， (已知) ∴∠ADB=∠ABC.(等角的补角相等).在△ABD与△ABC中，
∴ △ABD≌△ABC.(ASA)∴ DB=CB.(全等三角形的对应边相等)
例2 已知：如图，要测量河两岸相对的两点A，B之间的距离，可以在AB的垂线BF上取两点C，D(BF在河岸上)，使BC=CD，再过点D作BF的垂线DE，使点A，C，E在一条直线上，这时测得DE的长等于AB的长，请说明道理.
分析：题目要证明的是AB=DE.AB和DE分别在△ABC和△EDC中，所以要证AB=DE，只需证明△ABC≌△EDC.已知： ∠ABC=∠EDC=90°，(垂直定义)BC=CD，(已知)∠ACB=∠ECD.(对顶角相等)
我们在找相等的角时，注意隐含的条件相等的角——对顶角.
证明：∵AB⊥BD，ED⊥BD，(已知) ∴∠ABC=∠EDC=90°，(垂直定义)在△ABC和△EDC中，
∴ △ABC≌△EDC.(ASA)∴ AB=DE.(全等三角形的对应边相等)
1.如图，用纸板挡住了三角形的一部分，小明根据所学知识很快就画出了一个与原来完全一样的三角形，他的依据是( )
2.如图，∠ABC＝∠DCB，只需补充条件________________；就可以根据“ASA”得到△ABC≌△DCB.
3.如图，要测量池塘两岸相对的两点A，B的距离，可以在池塘外取AB的垂线BF上的两点C，D，使BC=CD，再画出BF的垂线DE，使E与A，C在一条直线上，这时测得DE的长就是AB的长.为什么?
两角及其夹边分别相等的两个三角形全等.简记为“角边角”或“ASA”.
教科书第102页练习题第1、2、3题