沪科版八年级上册11.1 平面上的点坐标教课内容ppt课件

这是一份沪科版八年级上册11.1 平面上的点坐标教课内容ppt课件，共25页。PPT课件主要包含了平面直角坐标系，吴小明25，王健53，点P的横坐标是–2，纵坐标是3，记作–23，–3–2，3–3，–30，A34等内容，欢迎下载使用。

1．知道有序实数对的概念，认识平面直角坐标系的相关知识．
2．理解坐标平面内的点与有序实数对的一一对应关系，能写出给定的平面直角坐标系中某一点的坐标，已知点的坐标，能在平面直角坐标系中描出点．
3．能在方格纸中建立适当的平面直角坐标系来描述点的位置．
4．通过引入有序实数对、平面直角坐标系让学生体会到现实生活中的问题的解决与数学的发展之间有联系，感受到数学的价值．
数轴上的点与实数是一一对应的
什么是数轴？请你试着画出一条数轴.
追问：A，B 两点所表示的数分别是什么？
A 点表示 – 4，B 点表示 2.
描一描：请你在上边的数轴上标出“–5”表示的点.
情境1：到电影院看电影，你是怎样找到具体位置的？
情境2：下图是北京环球影城的平面示意图，你能向游客描述一下每个景点的位置吗？
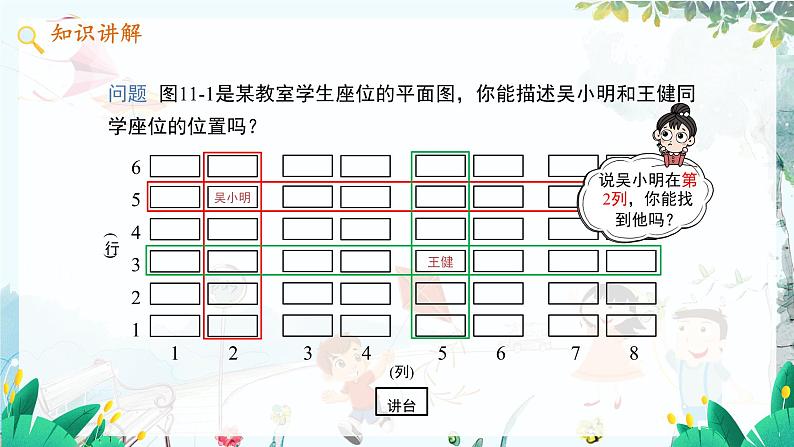
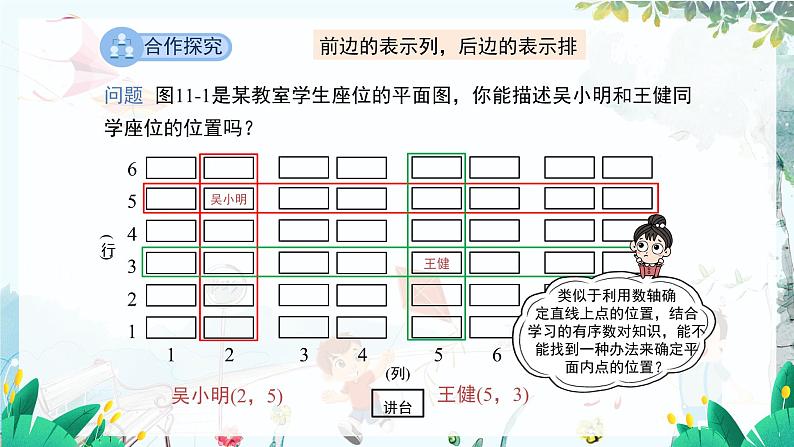
问题 图11-1是某教室学生座位的平面图，你能描述吴小明和王健同学座位的位置吗？
前边的表示列，后边的表示排
数学中，为了确定平面内一个点的位置，我们先在平面内画两条互相垂直并且原点重合的数轴，如上图．水平的数轴叫做x轴或横轴(x-axis)，取向右为正方向；垂直的数轴叫做y轴或纵轴(y-axis)，取向上为正方向；两轴交点O为原点．这样就建立了平面直角坐标系，这个平面叫做坐标平面．
横坐标在前，纵坐标在后
(–2，3)就叫做点P在平面直角坐标系中的坐标，简称点P的坐标，表示为P(–2，3).
平面直角坐标系内任意一点的坐标(x，y)的确定方法：从此点向x轴画垂线，垂足（垂线与x轴的交点）即是该点的横坐标(x)；从此点向y轴画垂线，垂足（垂线与y轴的交点）即是该点的纵坐标(y).
如何确定平面内点的位置？
1. 把下图中A，B，C，D，E，F各点对应的坐标填入下表：
注意：(4，2)和(2，4)表示的两个点是不同的，因为表示平面上的点的坐标是一个有序数对.
2. 在下图的平面直角坐标系中，描出下列各点：
A(3，4) ，B(3，–2) ，C(–1，–4) ，D(–2，2) ，E(2，0)，F(0，–3) .
坐标平面内任意一点P，都有唯一的一个有序数对(x，y)和它对应；对于任意一个有序实数对(x，y)，在坐标平面内都有唯一的一点P和它对应.
平面上的点和坐标是一一对应的.
点 O 的坐标是什么？x 轴和 y 轴上的点的坐标有什么特点？
一般记为(0，y) ；
一般记为(x，0) ;
观察平面直角坐标系，学习其各部分的名称和对应点的特点.
原点的坐标是：O(0，0)
x轴上的点：纵坐标都是 0
y轴上的点：横坐标都是 0
注意：坐标轴上的点不属于任何象限.
例1 如图，甲处表示 2 街与 5 巷的十字路口，乙处表示5街与2巷的十字路口.如果用（2，5）表示甲处的位置，那么“（2，5）→（3，5）→（4，5）→（5，5）→（5，4）→（5，3）→（5，2）”表示从甲处到乙处的一种路线.请你用这种形式写出几种从甲处到乙处的路线.
例2 在平面直角坐标系中描出下列各点:
A(4，5) ，B(–2，3) ，C(–4，–1) ，D(2.5，–2) ，E(0，–4) .
例3 点 M(a，b) 为平面直角坐标系中的点.(1) 当 a＞0，b＜0 时，点 M 位于第几象限？(2) 当 ab＞0 时，点M 位于第几象限？(3) 当 a 为任意实数，且 b＜0 时，点 M 位于第几象限？
解析：在平面直角坐标系内，点的坐标特点为：
原点的坐标是(0，0) ；
x轴上的点：纵坐标都是 0；
y轴上的点：横坐标都是 0；
坐标轴上的点不属于任何象限.
例3 点 M(a，b) 为平面直角坐标系中的点.(1) 当 a＞0，b＜0 时，点 M 位于第几象限？
例3 点 M(a，b) 为平面直角坐标系中的点.(2) 当 ab＞0 时，点M 位于第几象限？
a＞0，b＞0 时，点M在第一象限；
a＜0，b＜0 时，点M在第三象限.
例3 点 M(a，b) 为平面直角坐标系中的点.(3) 当 a 为任意实数，且 b＜0 时，点 M 位于第几象限？
a＜0，b＜0 时，点 M 在第三象限；
a＞0，b＜0 时，点 M 在第四象限；
a=0，b＜0 时，点 M 在 y 轴的负半轴.
1. 下列关于有序数对的说法正确的是（ ）
A. （3，4）与（4，3）表示的位置相同B. （a，b）与（b，a）表示的位置肯定不同C. （3，5）与（5，3）是表示不同位置的两个有序数对D. 有序数对（4，4）与（4，4）表示两个不同的位置
解析：因为有序数对是有顺序的，所以两个不同的数字，如果先后顺序不同，表示的位置肯定不同。对于选项 B，当 a，b 表示的数相同时，它们表示的位置相同.
2. 写出图中点 A，B，C，D，E，F 的坐标.
(1) 下列各点中，在第二象限的是( )
A.(2，3) B.(2，–3) C.(–2，–3) D.(– 2，3)
(2) 下列各点中，在 x 轴上的点是( )
A.(0，3) B.(–3，0) C.(–1，2) D.(–2，–3)
(1) 若 |a| = 5，|b| = 4，且点 M(a，b) 在第二象限，则点 M 的 坐标是 .
(2) 已知坐标平面内点 A(a，b) 在第四象限，那么点 B(b，a) 在第 象限，点 C(–a，–b) 在第 象限.
分析：由点 M 在第二象限得，a＜0，b＞0.又知道 |a| = 5，|b| = 4，所以 a = –5，b = 4.
分析：由点 A 在第四象限得，a＞0，b＜0，所以 –a＜0，–b＞0.所以点B(b，a) 在第二象限，点C(–a，–b) 也在第二象限.