
人教版七年级数学下册同步精品讲义专题第04课 平行线的性质及平移(教师版)
展开目标导航
知识精讲
知识点01 平行线的性质
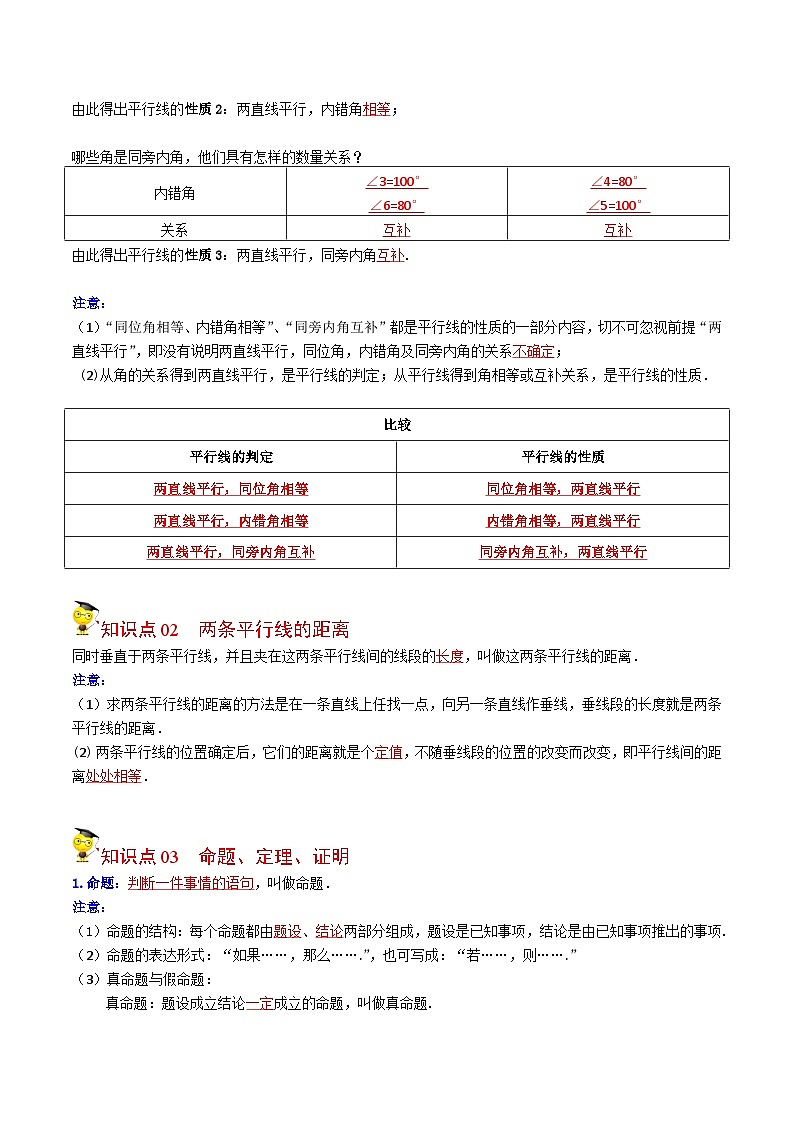
如右图:a∥b, 截线c与这两条平行线相交,他们相交所成的角分别为∠1, ∠2………. ∠8.测量他们的角并填入下表中。并回答下列问题
哪些角是同位角,他们具有怎样的数量关系?
由此得出平行线的性质1:两直线平行,同位角相等;
哪些角是 内错角,他们具有怎样的数量关系?
由此得出平行线的性质2:两直线平行,内错角相等;
哪些角是同旁内角,他们具有怎样的数量关系?
由此得出平行线的性质3:两直线平行,同旁内角互补.
注意:
(1)“同位角相等、内错角相等”、“同旁内角互补”都是平行线的性质的一部分内容,切不可忽视前提“两直线平行”,即没有说明两直线平行,同位角,内错角及同旁内角的关系不确定;
(2)从角的关系得到两直线平行,是平行线的判定;从平行线得到角相等或互补关系,是平行线的性质.
知识点02 两条平行线的距离
同时垂直于两条平行线,并且夹在这两条平行线间的线段的长度,叫做这两条平行线的距离.
注意:
(1)求两条平行线的距离的方法是在一条直线上任找一点,向另一条直线作垂线,垂线段的长度就是两条平行线的距离.
(2) 两条平行线的位置确定后,它们的距离就是个定值,不随垂线段的位置的改变而改变,即平行线间的距离处处相等.
知识点03 命题、定理、证明
1.命题:判断一件事情的语句,叫做命题.
注意:
(1)命题的结构:每个命题都由题设、结论两部分组成,题设是已知事项,结论是由已知事项推出的事项.
(2)命题的表达形式:“如果……,那么…….”,也可写成:“若……,则…….”
(3)真命题与假命题:
真命题:题设成立结论一定成立的命题,叫做真命题.
假命题:题设成立而不能保证结论一定成立的命题,叫做假命题.
2.定理:定理是从真命题(公理或其他已被证明的定理)出发,经过推理证实得到的另一个真命题,定理也可以作为继续推理的依据.
3.证明:在很多情况下,一个命题的正确性需要经过推理,才能作出判断,这个推理过程叫做证明.
注意:
(1)证明中的每一步推理都要有根据,不能“想当然”,这些根据可以是已知条件,学过的定义、基本事实、定理等.
(2)判断一个命题是正确的,必须经过严格的证明;判断一个命题是假命题,只需列举一个反例即可.
知识点04 平移
1. 定义:在平面内,将一个图形沿某个方向移动一定的距离,图形的这种移动叫做平移.
注意:
(1)图形的平移的两要素:平移的方向与平移的距离.
(2)图形的平移不改变图形的形状与大小,只改变图形的位置.
2. 性质:
图形的平移实质上是将图形上所有点沿同一方向移动相同的距离,平移不改变线段、角的大小,具体来说:
(1)平移后,对应线段平行且相等;
(2)平移后,对应角相等;
(3)平移后,对应点所连线段平行且相等;
(4)平移后,新图形与原图形是一对全等图形.
注意:
(1)“连接各组对应点的线段”的线段的长度实际上就是平移的距离.
(2)要注意“连接各组对应点的线段”与“对应线段”的区别,前者是通过连接平移前后的对应点得到的,而后者是原来的图形与平移后的图形上本身存在的.
3. 作图:
平移作图是平移基本性质的应用,在具体作图时,应抓住作图的“四步曲”——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点;
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(4)连:按原图形顺次连接对应点.
能力拓展
考法01 平行线的性质
【典例1】下列说法:
①在同一平面内,不相交的两条线段叫做平行线;
②过一点,有且只有一条直线平行于已知直线;
③两条平行直线被第三条直线所截,同位角相等;
④同旁内角相等,两直线平行.
正确的个数有( )个.
A.1B.2C.3D.4
【答案】A
【分析】
①根据平行线的定义进行判定;
②根据平行线的性质进行判定;
③根据平行线的性质定理进行判定,两条直线平行,同位角相等;
④根据平行线的判定定理进行判定,同旁内角互补两条直线平行.
【详解】
①在同一平面内,不相交的两条直线叫做平行线,故原命题错误;
②过直线外一点,有且只有一条直线平行于已知直线,故原命题错误;
③两条平行直线被第三条直线所截,同位角相等,正确;
④同旁内角互补,两直线平行,故原命题错误.
故选:A
【点睛】
本题考查了平行线的定义,平行线性质定理和平行线的判定定理.
【典例2】下列图形中,由AB∥CD,能得到∠1=∠2的是
A.B.C.D.
【答案】B
【详解】
分析:根据平行线的性质应用排除法求解:
A、∵AB∥CD,∴∠1+∠2=180°.故本选项错误.
B、如图,∵AB∥CD,∴∠1=∠3.
∵∠2=∠3,∴∠1=∠2.故本选项正确.
C、∵AB∥CD,∴∠BAD=∠CDA,不能得到∠1=∠2.故本选项错误.
D、当梯形ABDC是等腰梯形时才有,∠1=∠2.故本选项错误.
故选B.
【即学即练】如图,直线AB∥CD,则下列结论正确的是( )
A.∠1=∠2B.∠3=∠4C.∠1+∠3=180°D.∠3+∠4=180°
【答案】D
【详解】
分析:依据AB∥CD,可得∠3+∠5=180°,再根据∠5=∠4,即可得出∠3+∠4=180°.
详解:如图,∵AB∥CD,
∴∠3+∠5=180°,
又∵∠5=∠4,
∴∠3+∠4=180°,
故选D.
点睛:本题考查了平行线的性质,解题时注意:两直线平行,同旁内角互补.
【即学即练】如图,OC是∠AOB的角平分线,l//OB,若∠1=52°,则∠2的度数为( )
A.52°B.54°C.64°D.69°
【答案】C
【分析】
先根据两直线平行,同旁内角互补求出∠AOB=128°,再根据角平分线的定义得到∠BOC=64°,继而根据平行线的性质即可求得答案.
【详解】
∵l//OB,
∴∠1+∠AOB=180°,
∴∠AOB=128°,
∵OC平分∠AOB,
∴∠BOC=64°,
又∵l//OB,
∴∠2=∠BOC=64°,
故选C.
【点睛】
本题考查了平行线的性质,角平分线的定义,熟练掌握平行线的性质是解本题的关键.
【即学即练】如图,已知∠1=∠2,∠3=30°,则∠B的度数是( )
A.B.C.D.
【答案】B
【分析】
根据内错角相等,两直线平行,得AB∥CE,再根据性质得∠B=∠3.
【详解】
因为∠1=∠2,
所以AB∥CE
所以∠B=∠3=
故选B
【点睛】
熟练运用平行线的判定和性质.
【即学即练】如图,,,,则的度数是
A.B.C.D.
【答案】A
【分析】
直接利用平行线的性质结合等腰三角形的性质得出∠2的度数.
【详解】
,
,
,
,
=180°-∠ACD-∠CAD=,
故选A.
【点睛】
本题考查了平行线的性质和等腰三角形的性质,正确得出的度数是解题关键.
【即学即练】如图,直线AB、CD相交于点E,DF∥AB.若∠AEC=100°,则∠D等于( )
A.70°B.80°C.90°D.100°
【答案】B
【详解】
因为AB∥DF,所以∠D+∠DEB=180°,因为∠DEB与∠AEC是对顶角,
所以∠DEB=100°,所以∠D=180°﹣∠DEB=80°.故选B.
【即学即练】如图,,平分,若,则的度数为( )
A.B.C.D.
【答案】B
【分析】
根据平行线的性质可得,再根据角平分线的定义可得答案.
【详解】
∵,
∴,
∵平分,
∴,
故选B.
【点睛】
此题主要考查了平行线的性质,以及角平分线的定义,关键是掌握两直线平行,内错角相等.
【典例3】如图,将一块含有30°的直角三角板的顶点放在直尺的一边上,若∠1=48°,那么∠2的度数是( )
A.48°B.78°C.92°D.102°
【答案】D
【分析】
直接利用已知角的度数结合平行线的性质得出答案.
【详解】
解:如图:∵将一块含有30°的直角三角板的顶点放在直尺的一边上,∠1=48°,
∴∠2=∠3=180°﹣48°﹣30°=102°
故选D.
【点睛】
此题主要考查了平行线的性质,正确得出∠3的度数是解题关键.
【即学即练】将等腰直角三角形纸片和矩形纸片按如图方式折叠放在一起,若,则的度数为( )
A.B.C.D.
【答案】B
【分析】
根据平行的性质即可求解.
【详解】
根据平行线的性质得到∠3=∠1=30°,
∴∠2=45°-∠3=15°.
以及等腰直角三角形的性质,故选B
【点睛】
此题主要考查平行线的性质,解题的关键是熟知两直线平行,内错角相等.
【即学即练】如图,有一块含有30°角的直角三角形板的两个顶点放在直尺的对边上.如果∠2=44°,那么∠1的度数是( )
A.14°B.15°C.16°D.17°
【答案】C
【分析】
依据∠ABC=60°,∠2=44°,即可得到∠EBC=16°,再根据BE∥CD,即可得出∠1=∠EBC=16°.
【详解】
如图,
∵∠ABC=60°,∠2=44°,
∴∠EBC=16°,
∵BE∥CD,
∴∠1=∠EBC=16°,
故选C.
【点睛】
考查了平行线的性质,解题时注意:两直线平行,内错角相等.
【即学即练】把一块直尺与一块含的直角三角板如图放置,若,则的度数为( )
A.B.C.D.124°
【答案】D
【分析】
根据角的和差可先计算出∠AEF,再根据两直线平行同旁内角互补即可得出∠2的度数.
【详解】
解:由题意可知AD//BC,∠FEG=90°,
∵∠1=34°,∠FEG=90°,
∴∠AEF=90°-∠1=56°,
∵AD//BC,
∴∠2=180°-∠AEF=124°,
故选:D.
【点睛】
本题考查平行线的性质.熟练掌握两直线平行,同旁内角互补并能正确识图是解题关键.
考法02 辅助线与平行线
【典例4】如图,直线a∥b,将一个直角三角尺按如图所示的位置摆放,若∠1=58°,则∠2的度数为( )
A.30°B.32°C.42°D.58°
【答案】B
【详解】
试题分析:如图,过点A作AB∥b,∴∠3=∠1=58°,∵∠3+∠4=90°,∴∠4=90°﹣∠3=32°,∵a∥b,AB∥B,∴AB∥b,∴∠2=∠4=32°,故选B.
考点:平行线的性质.
【即学即练】如图,,,,则( )
A.B.C.D.
【答案】D
【分析】
过点E作,先根据平行线的判定可得,再根据平行线的性质分别可得和的度数,然后根据角的和差即可得.
【详解】
如图,过点E作,
,
,
又,
,
,
,
故选:D.
【点睛】
本题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解题关键.
【即学即练】如图,若AB∥CD,则α、β、γ之间的关系为( )
A.α+β+γ=360°B.α﹣β+γ=180°
C.α+β﹣γ=180°D.α+β+γ=180°
【答案】C
【分析】
过点E作EF∥AB,如图,易得CD∥EF,然后根据平行线的性质可得∠BAE+∠FEA=180°,∠C=∠FEC=γ,进一步即得结论.
【详解】
解:过点E作EF∥AB,如图,∵AB∥CD,AB∥EF,∴CD∥EF,
∴∠BAE+∠FEA=180°,∠C=∠FEC=γ,
∴∠FEA=β﹣γ,∴α+(β﹣γ)=180°,即α+β﹣γ=180°.
故选:C.
【点睛】
本题考查了平行公理的推论和平行线的性质,属于常考题型,作EF∥AB、熟练掌握平行线的性质是解题的关键.
【即学即练】如图,已知AB∥DE,∠ABC=70°,∠CDE=140°,则∠BCD的值为( )
A.20°B.30°C.40°D.70°
【答案】B
【详解】
试题分析:延长ED交BC于F,∵AB∥DE,∠ABC=70°,∴∠MFC=∠B=70°,∵∠CDE=140°,∴∠FDC=180°﹣140°=40°,∴∠C=∠MFC﹣∠MDC=70°﹣40°=30°,故选B.
考点:平行线的性质.
【即学即练】如图,已知AB∥CD∥EF,则∠、∠、∠三者之间的关系是( )
A.°B.°
C.°D.
【答案】B
【分析】
根据平行线的性质可得∠CEF=180°-y,x=z+∠CEF,利用等量代换可得x=z+180°-y,再变形即可.
【详解】
解:∵CD∥EF,
∴∠C+∠CEF=180°,
∴∠CEF=180°-y,
∵AB∥CD,
∴x=z+∠CEF,
∴x=z+180°-y,
∴x+y-z=180°,
故选:B.
【即学即练】如图,AB∥CD,则下列等式成立的是( )
A.∠B+∠F+∠D=∠E+∠GB.∠E+∠F+∠G=∠B+∠D
C.∠F+∠G+∠D=∠B+∠ED.∠B+∠E+∠F=∠G+∠D
【答案】A
【分析】
E作EM,过F作FH,过G作GH,推出AB,得出,,,,求出即可.
【详解】
过E作EM,过F作FH,过G作GN,
,.
,,
,
,
所以A选项是正确的.
【点睛】
本题主要考查了平行线的性质的应用,主要考查学生的推理能力.
【即学即练】如图,已知AB∥CD,则∠A、∠C、∠P的关系为_____.
【答案】∠A+∠C﹣∠P=180°
【详解】
如图所示,作PE∥CD,
∵PE∥CD,
∴∠C+∠CPE=180°,
又∵AB∥CD,
∴PE∥AB,
∴∠A=∠APE,
∴∠A+∠C-∠P=180°,
故答案是:∠A+∠C-∠P=180°.
【即学即练】珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,如图,若∠ABC=120°,∠BCD=80°,则∠CDE=__________度.
【答案】20
【分析】
由已知珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,得AB∥DE,过点C作CF∥AB,则CF∥DE,由平行线的性质可得,∠BCF+∠ABC=180°,所以能求出∠BCF,继而求出∠DCF,又由CF∥DE,所以∠CDE=∠DCF.
【详解】
解:过点C作CF∥AB,
已知珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,
∴AB∥DE,
∴CF∥DE,
∴∠BCF+∠ABC=180°,
∴∠BCF=60°,
∴∠DCF=20°,
∴∠CDE=∠DCF=20°.
故答案为20.
【点睛】
此题考查的知识点是平行线的性质,关键是过C点先作AB的平行线,由平行线的性质求解.
【即学即练】如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1等于( )
A.132°B.134°C.136°D.138°
【答案】B
【详解】
过E作EF∥AB,求出AB∥CD∥EF,根据平行线的性质得出∠C=∠FEC,∠BAE=∠FEA,求出∠BAE,即可求出答案.
解:
过E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠C=∠FEC,∠BAE=∠FEA,
∵∠C=44°,∠AEC为直角,
∴∠FEC=44°,∠BAE=∠AEF=90°﹣44°=46°,
∴∠1=180°﹣∠BAE=180°﹣46°=134°,
故选B.
“点睛”本题考查了平行线的性质的应用,能正确作出辅助线是解此题的关键.
【即学即练】如图,已知AB,CD,EF互相平行,且∠ABE=70°,∠ECD=150°,则∠BEC=________°.
【答案】40
【详解】
根据平行线的性质,先求出∠BEF和∠CEF的度数,再求出它们的差就可以了.
解:∵AB∥EF,
∴∠BEF=∠ABE=70°;
又∵EF∥CD,
∴∠CEF=180°-∠ECD=180°-150°=30°,
∴∠BEC=∠BEF-∠CEF=40°;
故应填40.
“点睛”本题主要利用两直线平行,同旁内角互补以及两直线平行,内错角相等进行解题.
考法03 折叠问题
【典例5】如图折叠一张矩形纸片,已知∠1=70°,则∠2的度数是__.
【答案】55°
【详解】
, , .
【即学即练】如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于( )
A.112°B.110°C.108°D.106°
【答案】D
【详解】
分析:由折叠可得:∠DGH=∠DGE=74°,再根据AD∥BC,即可得到∠GHC=180°﹣∠DGH=106°.
详解:∵∠AGE=32°,
∴∠DGE=148°,
由折叠可得:∠DGH=∠DGE=74°.
∵AD∥BC,
∴∠GHC=180°﹣∠DGH=106°.
故选D.
点睛:本题主要考查了平行线的性质,解题时注意:两直线平行,同旁内角互补.
【即学即练】如图所示,把一张长方形纸片沿折叠后,点分别落在点的位置.若,则等于________.
【答案】50°
【分析】
先根据平行线的性质得出∠DEF的度数,再根据翻折变换的性质得出∠D′EF的度数,根据平角的定义即可得出结论.
【详解】
∵AD∥BC,∠EFB=65°,
∴∠DEF=65°,
又∵∠DEF=∠D′EF,
∴∠D′EF=65°,
∴∠AED′=50°.
【点睛】
本题考查翻折变换(折叠问题)和平行线的性质,解题的关键是掌握翻折变换(折叠问题)和平行线的性质.
【即学即练】将一个矩形纸片按如图所示折叠,若∠1=40°,则∠2的度数是( )
A.40°B.50°C.60°D.70°
【答案】D
【分析】
根据折叠的知识和直线平行判定即可解答.
【详解】
解:如图可知折叠后的图案∠ABC=∠EBC,
又因为矩形对边平行,根据直线平行内错角相等可得
∠2=∠DBC,
又因为∠2+∠ABC=180°,
所以∠EBC+∠2=180°,
即∠DBC+∠2=2∠2=180°-∠1=140°.
可求出∠2=70°.
【点睛】
掌握折叠图形的过程中有些角度是对称相等的是解答本题的关键.
【即学即练】如图,一个宽度相等的纸条按如图所示方法折叠一下,则________度.
【答案】65
【分析】
根据两直线平行内错角相等,以及折叠关系列出方程求解则可.
【详解】
解:如图,由题意可知,
AB∥CD,
∴∠1+∠2=130°,
由折叠可知,∠1=∠2,
∴2∠1=130°,
解得∠1=65°.
故答案为:65.
【点睛】
本题考查了平行线的性质和折叠的知识,题目比较灵活,难度一般.
【即学即练】如图,将一张长方形纸片ABCD沿EF折叠,使顶点C,D分别落在点C′、D′处,C′E交AF于点G,若∠CEF=64°,则∠GFD′=_____________.
【答案】520
【解析】
因为AD∥BC,所以∠CEF=∠AFE=64°,∠DFE=180°-∠CEF=180°-64°=116°,由折叠得∠EFD=∠EFD′,所以∠EFD′=116°,所以∠GFD′=∠EFD′-∠AFE=116°-64°=52°,故答案为52°.
【即学即练】如图,把长方形ABCD沿EF对折,若∠1=500,则∠AEF的度数等于__.
【答案】
【详解】
∵把矩形ABCD沿EF对折,∴AD∥BC,∠BFE=∠2,
∵∠1=50°,∠1+∠2+∠BFE=180°,∴∠BFE==65°,
∵∠AEF+∠BFE=180°,∴∠AEF=115°.
故答案为115°.
考法04 综合证明
【典例6】如图,已知,,试说明直线AD与BC垂直请在下面的解答过程的空格内填空或在括号内填写理由.
理由:,已知
____________,______
____________
又,已知
______等量代换
____________,______
______
,已知
,,
____________.
【答案】GD AC 同位角相等,两直线平行 两直线平行,内错角相等 AD EF 同旁内角互补,两直线平行 两直线平行,同位角相等 AD BC
【解析】
【分析】
结合图形,根据平行线的判定和性质逐一进行填空即可.
【详解】
解:,已知
,同位角相等,两直线平行
两直线平行,内错角相等
又,已知
等量代换
,同旁内角互补,两直线平行
两直线平行,同位角相等
,已知
,
,
.
【点睛】
本题主要考查了平行线的判定和性质,已经垂线的定义,解答此题的关键是注意平行线的性质和判定定理的综合运用.
【即学即练】如图,已知AC∥DF,直线AF分别与直线BD、CE相交于点G,H,∠1=∠2.求证:∠C=∠D.
解:∵∠1=∠2(已知)
∠1=∠DGH( ),
∴∠2=_______( 等量代换 )
∴_______∥_______(同位角相等,两直线平行)
∴∠C=_______(两直线平行,同位角相等)
又∵AC∥DF( )
∴∠D=∠ABG ( )
∴∠C=∠D ( )
【答案】对顶角相等 ,∠DGH, BD∥CE ,∠ABG, 已知,两直线平行,内错角相等,等量代换,
【详解】
整体分析:
根据平行线的性质,判定和对顶角相等解题,注意理解图形.
证明:∵∠1=∠2(已知)
∠1=∠DGH(对顶角相等),
∴∠2=∠DGH(等量代换)
∴BD∥CE(同位角相等,两直线平行)
∴∠C=∠ABG(两直线平行,同位角相等)
又∵AC∥DF(已知)
∴∠D=∠ABG(两直线平行,内错角相等)
∴∠C=∠D(等量代换).
【即学即练】如图,已知在△ABC中,EF⊥AB,CD⊥AB,G在AC边上,∠AGD=∠ACB,求证:∠1=∠2.
【答案】见解析.
【分析】
由EF⊥AB,CD⊥AB可得EF∥CD,由∠AGD=∠ACB可得DG∥BC.再利用平行线的性质可证∠1=∠2.
【详解】
∵EF⊥AB,CD⊥AB,
∴EF∥CD,
∴∠2=∠3.
又∵∠AGD=∠ACB,
∴DG∥BC,
∴∠1=∠3;
∴∠1=∠2.
【点睛】
本题考查了平行线的判定与性质,掌握平行线的判定和性质是解题的关键.
【即学即练】如图,AE⊥BC,FG⊥BC,∠1=∠2,求证:AB∥CD.
【答案】见解析
【分析】
首先由AE⊥BC,FG⊥BC可得AE∥FG,根据两直线平行,同位角相等及等量代换可推出∠A=∠2,利用内错角相等,两直线平行可得AB∥CD.
【详解】
证明:如图,设BC与AE、GF分别交于点M、N.
∵AE⊥BC,FG⊥BC,
∴∠AMB=∠GNB=90°,
∴AE∥FG,
∴∠A=∠1;
又∵∠2=∠1,
∴∠A=∠2,
∴AB∥CD.
【点睛】
本题考查了平行线的性质及判定,熟记定理是正确解题的关键.
考法05 命题
【典例7】把命题“等角的补角相等”改写成“如果…那么…”的形式是______.
【答案】如果两个角是等角的补角,那么它们相等.
【分析】
弄清命题的题设(条件)和结论即可写出.
【详解】
解:题设为:两个角是等角的补角,结论为:相等,故写成“如果…那么…”的形式是:如果两个角是等角的补角,那么它们相等.
故答案为如果两个角是等角的补角,那么它们相等.
【点睛】
本题考查了将原命题写成“如果…那么…”即题设(条件)与结论的形式,解决问题的关键是找出相应的题设和结论.
【即学即练】将“平行于同一条直线的两条直线平行”改写成“如果……那么……”的形式为_________________________________________________.
【答案】如果两条直线平行于同一条直线,那么这两条直线平行.
【分析】
命题由题设和结论两部分组成,通常写成“如果…那么…”的形式.“如果”后面接题设,“那么”后面接结论.
【详解】
命题可以改写为:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
【点睛】
任何一个命题都可以写成“如果…那么…”的形式.“如果”后面接题设,“那么”后面接结论.在改写过程中,不能简单地把题设部分、结论部分分别塞在“如果”、“那么”后面,要适当增减词语,保证句子通顺而不改变原意.
【即学即练】下列命题是真命题的是( )
A.如果一个数的相反数等于这个数本身,那么这个数一定是0
B.如果一个数的倒数等于这个数本身,那么这个数一定是1
C.如果一个数的平方等于这个数本身,那么这个数一定是0
D.如果一个数的算术平方根等于这个数本身,那么这个数一定是0
【答案】A
【分析】
根据相反数是它本身的数为0;倒数等于这个数本身是±1;平方等于它本身的数为1和0;算术平方根等于本身的数为1和0进行分析即可.
【详解】
A、如果一个数的相反数等于这个数本身,那么这个数一定是0,是真命题;
B、如果一个数的倒数等于这个数本身,那么这个数一定是1,是假命题;
C、如果一个数的平方等于这个数本身,那么这个数一定是0,是假命题;
D、如果一个数的算术平方根等于这个数本身,那么这个数一定是0,是假命题;
故选A.
【点睛】
此题主要考查了命题与定理,关键是掌握正确的命题为真命题,错误的命题为假命题.
【即学即练】将“对顶角相等”改写为“如果...那么...”的形式,可写为__________.
【答案】如果两个角互为对顶角,那么这两个角相等
【分析】
根据命题的形式解答即可.
【详解】
将“对顶角相等”改写为“如果...那么...”的形式,可写为如果两个角互为对顶角,那么这两个角相等,
故答案为:如果两个角互为对顶角,那么这两个角相等.
【点睛】
此题考查命题的形式,可写成用关联词“如果...那么...”连接的形式,准确确定命题中的题设和结论是解题的关键.
【即学即练】将命题“同角的补角相等”改写成“如果……,那么……”的形式为_________________.
【答案】如果两个角是同一个角的补角,那么这两个角相等
【详解】
试题考查知识点:命题改写
思路分析:每一个命题都是基于条件的一个判断,只要把条件部分和判断部分分开即可
具体解答过程:
如果两个角是同一个角的补角,那么这两个角相等
试题点评:这是关于命题的基本题型.
考法06 平移
【典例8】如图,A,B,C,D中的哪幅图案可以通过图案①平移得到( )
A.B.C.D.
【答案】D
【分析】
根据平移的性质,不改变图形的形状和大小,经过平移,对应点所连的线段平行且相等,对应线段平行且相等.
【详解】
通过图案①平移得到必须与图案①完全相同,角度也必须相同,
观察图形可知D可以通过图案①平移得到.
故答案选:D.
【点睛】
本题考查的知识点是生活中的平移现象,解题的关键是熟练的掌握生活中的平移现象.
【典例9】如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是( )
A.16cmB.18cmC.20cmD.21cm
【答案】C
【详解】
试题分析:已知,△ABE向右平移2cm得到△DCF,根据平移的性质得到EF=AD=2cm,AE=DF,又因△ABE的周长为16cm,所以AB+BC+AC=16cm,则四边形ABFD的周长=AB+BC+CF+DF+AD=16cm+2cm+2cm=20cm.故答案选C.
考点:平移的性质.
【即学即练】如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,∠B=90°,AB=8,DH=3,平移距离为4,求阴影部分的面积为( )
A.20B.24C.25D.26
【答案】D
【详解】
由平移的性质知,BE=4,DE=AB=8,可得HE=DE-DH=8-3=5,所以S四边形HDFC=S梯形ABEH=(AB+EH)×BE=(8+5)×4=26.故选D.
【即学即练】如图,有a、b、c三户家用电路接入电表,相邻电路的电线等距排列,则三户所用电线( )
A.a户最长B.b户最长C.c户最长D.三户一样长
【答案】D
【详解】
可理解为将最左边一组电线向右平移所得,由平移的性质即可得出结论.
∵a、b、c三户家用电路接入电表,相邻电路的电线等距排列,
∴将a向右平移即可得到b、c,
∵图形的平移不改变图形的大小,
∴三户一样长.
故选D.
【即学即练】如图,两只蚂蚁以相同的速度沿两条不同的路径,同时从A出发爬到B,则( )
A.乙比甲先到B.甲和乙同时到C.甲比乙先到D.无法确定
【答案】B
【分析】
根据平移可得出两蚂蚁行程相同,结合二者速度相同即可得出结论.
【详解】
如图:根据平移可得两只蚂蚁的行程相同,
∵甲、乙两只蚂蚁的行程相同,且两只蚂蚁的速度相同,
∴两只蚂蚁同时到达.
故选B.
【点睛】
本题考查了生活中的平移现象,结合图形找出甲、乙两只蚂蚁的行程相等是解题的关键.
【即学即练】如图是一块长方形的场地,长,宽,从、两处入口的中路宽都为,两小路汇合处路宽为,其余部分种植草坪,则草坪面积为( )
A.m2B.m2C.m2D.m2
【答案】B
【详解】
解:由图可知:矩形ABCD中去掉小路后,草坪正好可以拼成一个新的矩形,且它的长为:(102-2)米,宽为(51-1)米.
所以草坪的面积应该是长×宽=(102-2)(51-1)=5000(米2).
故选B.
【即学即练】如图,△ABC沿着由点B到点E的方向,平移到△DEF,已知BC=5.EC=3,那么平移的距离为( )
A.2B.3C.5D.7
【答案】A
【详解】
试题分析:观察图象,发现平移前后,B、E对应,C、F对应,根据平移的性质,易得平移的距离=BE=5﹣3=2.
故选A.
考点:平移的性质.
【即学即练】如图,已知∠1=75°,将直线m平行移动到直线n的位置,则∠2﹣∠3=_____°.
【答案】105
【分析】
直接利用平移的性质结合三角形外角的性质得出答案.
【详解】
由题意可得:m∥n,则∠CAD+∠1=180°.
∵∠3=∠4,∴∠4+∠CAD=∠2,∴∠2﹣∠3=∠CAD+∠3﹣∠3=∠CAD=180°﹣∠1=180°﹣75°=105°.
故答案为105.
【点睛】
本题考查了平移的性质、三角形外角的性质以及平行线的性质,正确转化角的关系是解题的关键.
【即学即练】某宾馆在重新装修后,准备在大厅的主楼梯上铺上红色地毯,已知这种红色地毯的售价为每平方米32元,主楼道宽2米,其侧面与正面如图所示,则购买地毯至少需______元.
【答案】512元
【分析】
根据题意,结合图形,先把楼梯的横竖向上向左平移,构成一个矩形,再求得其面积,则购买地毯的钱数可求.
【详解】
解:利用平移线段,把楼梯的横竖向上向左平移,构成一个长方形,长宽分别为5米,3米,∴地毯的长度为5+3=8(米),
∴地毯的面积为8×2=16(平方米),
∴买地毯至少需要16×32=512(元)
【点睛】
本题考查平移性质的实际运用.解决此题的关键是要利用平移的知识,把要求的所有线段平移到一条直线上进行计算.
【即学即练】如图,在长方形草地内修建了宽为2米的道路,则草地面积为_______米2.
【答案】144
【分析】
先求出道路的总长度,进而求出道路的面积,最后用总面积减去道路的面积即可.
【详解】
解:由图形得到了的总长度为20+10-2=28米,
所以道路的总面积为28×2=56米2,
所以草地面积为20×10-56=144米2.
故答案为:144
【点睛】
本题考查了请不规则图形的面积,根据题意求出道路的总长度是解题关键,注意应减去重合的部分.
分层提分
题组A 基础过关练
1.下列图形中,能将其中一个三角形平移得到另一个三角形的是( )
A.B.C.D.
【答案】A
【分析】
利用平移的性质,结合轴对称、旋转变换和位似图形的定义判断得出即可.
【详解】
A、可以通过平移得到,故此选项正确;
B、可以通过旋转得到,故此选项错误;
C、是位似图形,故此选项错误;
D、可以通过轴对称得到,故此选项错误;
故选A.
【点睛】
本题考查了平移的性质以及轴对称、旋转变换和位似图形,正确把握定义是解题的关键.
2.如图,直线a,b被直线c所截,a//b,∠1=60°,则∠2的度数是( )
A.120°B.60°C.45°D.30°
【答案】B
【解析】
分析:根据平行线的性质可得解.
详解:∵a//b
∴∠1=∠2
又∵∠1=60°,
∴∠2=60°
故选B.
点睛:两条平行线被第三条直线所截,同位角相等.
3.如图,将一张含有角的三角形纸片的两个顶点叠放在矩形的两条对边上,若,则的大小为( )
A.B.C.D.
【答案】A
【详解】
分析:依据平行线的性质,即可得到∠2=∠3=44°,再根据三角形外角性质,可得∠3=∠1+30°,进而得出结论.
详解:如图,∵矩形的对边平行,∴∠2=∠3=44°,根据三角形外角性质,可得:∠3=∠1+30°,∴∠1=44°﹣30°=14°.
故选A.
点睛:本题主要考查了平行线的性质以及三角形外角性质的运用,解题时注意:两直线平行,同位角相等.
4.如图,∠1=∠2,AC平分∠DAB,且∠D:∠DAB=2:1,则∠D的度数是( )
A.120°B.130°C.140°D.150°
【答案】A
【分析】
先证明DC∥AB,得到∠D+∠DAB=180°,再根据∠D:∠DAB=2:1即可求解.
【详解】
解:∵AC平分∠DAB,
∴∠1=∠CAB,
∵∠1=∠2,
∴∠CAB=∠2,
∴DC∥AB,
∴∠D+∠DAB=180°,
又∵∠D:∠DAB=2:1,
∴∠D=180°×=120°.
故选:A
【点睛】
本题考查了平行线的性质与判定,熟练掌握平行线的性质定理和判定定理是解题关键.
5.如图,直线,将一块含角()的直角三角尺按图中方式放置,其中和两点分别落在直线和上.若,则的度数为( )
A.B.C.D.
【答案】C
【分析】
直接利用平行线的性质结合三角形内角和定理得出答案.
【详解】
解:直线,
,
,,,
.
故选C.
【点睛】
本题主要考查平行线的性质和定理,这是几何中的必考点,必须熟练掌握.
6.如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐弯处的∠A是72°,第二次拐弯处的角是∠B,第三次拐弯处的∠C是153°,这时道路恰好和第一次拐弯之前的道路平行,则∠B等于( )
A.81°B.99°C.108°D.120°
【答案】B
【详解】
试题解析:过B作BD∥AE,
∵AE∥CF,
∴BD∥CF,
∴
∵,
∴
则
故选B.
7.下列说法不正确的是( )
A.若两个相等的角有一组边平行,则另一组边也平行
B.两条直线相交,所成的两组对顶角的平分线互相垂直
C.两条平行线被第三条直线所截,同旁内角的平分线互相垂直
D.经过直线外一点,有且只有一条直线与已知直线平行
【答案】A
【分析】
根据对顶角的定义,平行线的性质,垂线的性质分别进行分析即可.
【详解】
A、若两相等的角有一边平行,则另一边也互相平行或者相交,所以说法错误;
B、两条直线相交,所成的两组对顶角的平分线互相垂直,正确;
C、两条平行线被第三条直线所截,同旁内角的平分线互相垂直,正确;
D、经过直线外一点,有且只有一条直线与已知直线平行,正确,
故选A.
【点睛】
本题考查了命题与定理的知识,解题的关键是了解对顶角的定义,平行线的性质,垂线的性质等知识,难度不大.
题组B 能力提升练
1.把命题“两直线平行,内错角相等”改成“如果……那么……”的形式:____________________
【答案】如果两直线平行,那么内错角相等
【分析】
根据命题“两直线平行,内错角相等”的题设和结论进行分析解答即可.
【详解】
把命题“两直线平行,内错角相等”改写成“如果那么”的形式为:
如果两直线平行,那么内错角相等.
【点睛】
知道命题“两直线平行,内错角相等”的题设是“两直线平行”,结论是“内错角相等”是解答本题的关键.
2.如图,一条公路修到湖边时,需拐弯绕湖而过,在A,B,C三处经过三次拐弯,此时道路恰好和第一次拐弯之前的道路平行(即AE∥CD),若∠A=120°,∠B=150°,则∠C的度数是________
【答案】150°
【详解】
如图,过点B作BG∥AE,
因为AE∥CD,所以AE∥BG∥CD.
所以∠A=∠2,∠1+∠C=180°.
因为∠A=120°,所以∠2=120°,所以∠1=150°-120°=30°.
所以∠C=180°-30°=150°,故答案为150°.
3.如图,三角板直角顶点落在长方形纸片的一边上,∠1=35°,则∠2=_____°.
【答案】55.
【分析】
由平角的定义求出∠3=55°,再根据平行线的性质即可解决问题.
【详解】
解:∵∠1+∠3=90°,∠1=35°,
∴∠3=55°,
∵AB//CD
∴∠2=∠3=55°,
故答案是:55.
【点睛】
此题考查了平行线的性质.两直线平行,同位角相等的应用是解此题的关键.
4.如图所示,把长方形ABCD沿EF折叠,若∠1=48°,则∠AEF等于______.
【答案】114°
【解析】
【分析】
根据折叠性质求出∠2和∠3,根据平行线性质求出∠AEF+∠2=180°,代入求出即可.
【详解】
根据折叠性质得出∠2=∠3=(180°-∠1)=×(180°-48°)=66°,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AEF+∠2=180°,
∴∠AEF=114°,
故答案为:114°.
【点睛】
本题考查了矩形性质,平行线性质,折叠性质的应用,关键是求出∠2的度数和得出∠AEF+∠2=180°.
5.在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)
如图,已知AB∥CD,BE、CF分别平分∠ABC和∠DCB,求证:BE∥CF.
证明:∵AB∥CD,(已知)
∴∠_______=∠_______.___________________________
∵__________________________________________,(已知)
∴∠EBC=_______,(角平分线定义)
同理,∠FCB=______________.
∴∠EBC=∠FCB.(等式性质)
∴BE//CF.(_____________________________________)
【答案】ABC DCB 两直线平行,内错角相等 BE平分∠ABC ∠ABC ∠DCB 内错角相等,两直线平行
【分析】
根据平行线的性质得出∠ABC=∠DCB,求出∠EBC=∠FCB,根据平行线的判定得出即可.
【详解】
∵AB∥CD(已知)
∴∠ABC=∠DCB(两直线平行,内错角相等).
∵BE平分∠ABC(已知),∴∠EBC∠ABC(角平分线的定义)
同理:∠FCB∠DCB,∴∠FBC=∠FCB(等式性质),∴BE∥CF(内错角相等,两直线平行).
故答案为ABC;DCB;两直线平行,内错角相等;BE平分∠ABC;∠ABC;∠DCB;内错角相等,两直线平行.
【点睛】
本题考查了平行线的性质和判定、角平分线的定义等知识点,能熟练地运用定理进行推理是解答此题的关键.
6.阅读理解,补全证明过程及推理依据.
已知:如图,点E在直线DF上,点B在直线AC上,∠1=∠2,∠3=∠4.
求证:∠A=∠F.
证明:∵∠1=∠2(已知)
∠2=∠DGF( )
∴∠1=∠DGF(等量代换)
∴BD ( )
∴∠3+∠ =180°( )
又∵∠3=∠4(已知)
∴∠4+∠C=180°(等量代换)
∴ DF( )
∴∠A=∠F( )
【答案】对顶角相等;CE;同位角相等,两直线平行;C;两直线平行,同旁内角互补;AC(或AB);同旁内角互补,两直线平行;两直线平行,内错角相等
【分析】
先证明BDCE,得出同旁内角互补∠3+∠C=180°,再由已知得出∠4+∠C=180°,证出 ACDF,即可得出结论.
【详解】
解:∵∠1=∠2(已知)
∠2=∠DGF(对顶角相等)
∴∠1=∠DGF( 等量代换 )
∴BDCE (同位角相等,两直线平行)
∴∠3+∠C =180°(两直线平行,同旁内角互补)
又∵∠3=∠4(已知)
∴∠4+∠C=180°(等量代换)
∴AC(或AB) DF(同旁内角互补,两直线平行)
∴∠A=∠F(两直线平行,内错角相等).
【点睛】
本题考查了平行线的判定与性质、对顶角相等的性质;熟练掌握平行线的判定与性质是解决问题的关键.
题组C 培优拔尖练
1.如图,已知,.
求证:;
若,且,求的度数.
【答案】(1)证明见解析;(2)∠B=50°.
【解析】
【分析】
欲证明,只需证出即可;
利用平行线的判定定理证明出,然后由平行线的性质即可得到结论.
【详解】
,,
又,
,
;
,
又,
,
,
,.
,
,
.
【点睛】
本题考查了平行线的判定,解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.
2.如图,,,,求证:.
【答案】证明见解析.
【分析】
先由已知证明AD∥EF,得到∠2=∠CAD,再证明AC∥DG,得到∠1=∠CAD,等量代换得出∠1=∠2.
【详解】
证明:∵AD⊥BC,EF⊥BC,
∴AD∥EF,
∴∠2=∠CAD,
又∵∠3=∠C,
∴AC∥DG,
∴∠1=∠CAD,
∴∠1=∠2.
【点睛】
本题主要考查了平行线的性质及判定.熟知:①两直线平行,同位角相等;②两直线平行,内错角相等是解题关键.
3.已知:如图,点D,E,F分别在线段AB,BC,AC上,连接DE、EF,DM平分∠ADE交EF于点M,∠1=∠2.求证:∠B+∠DEC=180°.
【答案】见解析
【解析】
【分析】
先根据∠1=∠2,证得DM∥BC;然后再运用平行的性质、三角形的外角的性质以及角平分线的性质列出等量关系,运用等量代换的方法,最后通过平角就是180°,从而完成证明.
【详解】
证明:∵∠1=∠2
∴DM∥BC
∴∠B=∠ADM,∠MDE=∠BED.
又∵∠DEC=∠B+∠BDE=∠1+∠DEM
∴∠DEC=∠ADM+∠BDE
又∵∠EDM=∠ADM
∴∠DEC=∠EDB+∠MDE
∴∠B+∠DEC=∠ADM +∠EDB+∠MDE =180°
【点睛】
本题主要考查了平行线的性质与判定的综合应用,解题时注意:平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.
4.已知,直线AB∥CD,E为AB、CD间的一点,连接EA、EC.
(1)如图①,若∠A=20°,∠C=40°,则∠AEC=______°.
(2)如图②,若∠A=x°,∠C=y°,则∠AEC=______°.
(3)如图③,若∠A=α,∠C=β,则α,β与∠AEC之间有何等量关系.并简要说明.
【答案】(1)60;(2) 360°﹣x°﹣y°(3)详见解析
【解析】
分析:首先都需要过点E作EF∥AB,由AB∥CD,可得AB∥CD∥EF.
(1)根据两直线平行,内错角相等,即可求得∠AEC的度数;
(2)根据两直线平行,同旁内角互补,即可求得∠AEC的度数;
(3)根据两直线平行,内错角相等;两直线平行,同旁内角互补,即可求得∠AEC的度数.
详解:如图,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF.
(1)∵∠A=20°,∠C=40°,
∴∠1=∠A=20°,∠2=∠C=40°,
∴∠AEC=∠1+∠2=60°;
(2)∴∠1+∠A=180°,∠2+∠C=180°,
∵∠A=x°,∠C=y°,
∴∠1+∠2+x°+y°=360°,
∴∠AEC=360°﹣x°﹣y°;
(3)∠A=α,∠C=β,
∴∠1+∠A=180°,∠2=∠C=β,
∴∠1=180°﹣∠A=180°﹣α,
∴∠AEC=∠1+∠2=180°﹣α+β.
点睛:此题考查了平行线的性质:两直线平行,内错角相等;两直线平行,同旁内角互补.解此题的关键是准确作出辅助线:作平行线,这是此类题目的常见解法.
课程标准
1.掌握平行线的性质,并能依据平行线的性质进行简单的推理;
2.了解平行线的判定与性质的区别和联系,理解两条平行线的距离的概念;
3. 掌握命题的定义,知道一个命题是由“题设”和“结论”两部分组成,对于给定的命题,能找出它的题设和结论;
4.了解图形的平移变换,知道一个图形进行平移后所得的图形与原图形之间所具有的联系和性质,能用平移变换有关知识说明一些简单问题及进行图形设计.
角
∠1
∠2
∠3
∠4
∠5
∠6
∠7
∠8
度数
100°
80°
100°
80°
100°
80°
100°
80°
同位角
∠1=100°
∠5=100°
∠2=80°
∠2=80°
∠3=100°
∠7=100°
∠4=80°
∠8=80°
关系
相等
相等
相等
相等
内错角
∠3=100°
∠5=100°
∠4=80°
∠6=80°
关系
相等
相等
内错角
∠3=100°
∠6=80°
∠4=80°
∠5=100°
关系
互补
互补
比较
平行线的判定
平行线的性质
两直线平行,同位角相等
同位角相等,两直线平行
两直线平行,内错角相等
内错角相等,两直线平行
两直线平行,同旁内角互补
同旁内角互补,两直线平行
人教版七年级数学下册同步精品讲义专题第29课 直方图(教师版): 这是一份人教版七年级数学下册同步精品讲义专题第29课 直方图(教师版),共19页。试卷主要包含了组距,频数,频数分布表,已知一组数据等内容,欢迎下载使用。
人教版七年级数学下册同步精品讲义专题第11课 实数单元检测(教师版): 这是一份人教版七年级数学下册同步精品讲义专题第11课 实数单元检测(教师版),共15页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
人教版七年级数学下册同步精品讲义专题第09课 实数(教师版)-: 这是一份人教版七年级数学下册同步精品讲义专题第09课 实数(教师版)-,共17页。试卷主要包含了313113111……,实数与数轴上的点一一对应,3737737773……等内容,欢迎下载使用。












