2025高考数学一轮复习-2.9-函数模型及其应用【课件】

这是一份2025高考数学一轮复习-2.9-函数模型及其应用【课件】，共60页。PPT课件主要包含了知识诊断基础夯实，BCD，考点突破题型剖析，当x≥8时，分层训练巩固提升，ABC等内容，欢迎下载使用。
ZHISHIZHENDUANJICHUHANGSHI
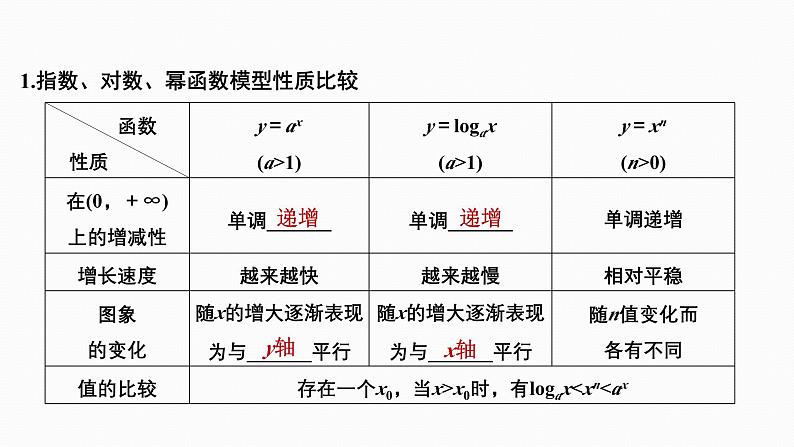
1.指数、对数、幂函数模型性质比较
2.几种常见的函数模型
1.“直线上升”是匀速增长，其增长量固定不变；“指数增长”先慢后快，其增长量成倍增加，常用“指数爆炸”来形容；“对数增长”先快后慢，其增长量越来越小.2.充分理解题意，并熟练掌握几种常见函数的图象和性质是解题的关键.3.易忽视实际问题中自变量的取值范围，需合理确定函数的定义域，必须验证数学结果对实际问题的合理性.
∴每件赔1元，(1)错误.(2)当x＝2时，2x＝x2＝4.不正确.
所以该同学视力的小数记录法的数据约为0.8.
根据该折线图，下列结论正确的是(　　 )A.月接待游客量逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7，8月D.各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳
3.(多选)某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量(单位：万人)的数据，绘制了下面的折线图.
解析　由题图可知，2014年8月到9月的月接待游客量在减少，则A错误.其余全部正确.
解析　设销售价每瓶定为x元，利润为y元，
4.某商店每月按出厂价每瓶3元购进一种饮料，根据以前的统计数据，若零售价定为每瓶4元，每月可销售400瓶；若零售价每降低(升高)0.5元，则可多(少)销售40瓶，在每月的进货当月销售完的前提下，为获得最大利润，销售价应定为(　　)元/瓶 B.7.5元/瓶C.12元/瓶 D.6元/瓶
所以x＝6时，y取得最大值.
则对x，y最适合的拟合函数是(　　)A.y＝2x B.y＝x2－1C.y＝2x－2 D.y＝lg2x
5.在某个物理实验中，测量得变量x和变量y的几组数据，如下表：
解析　当x＝0.99时，y＝0.01，可排除A，当x＝2.01时，y＝0.98，可排除B、C，故选D.
KAODIANTUPOTIXINGPOUXI
根据折线图，下列结论正确的是(　　)A.月跑步平均里程的中位数为6月份对应的平均里程数B.月跑步平均里程逐月增加C.月跑步平均里程高峰期大致在8月和9月D.1月至5月的月跑步平均里程相对于6月至11月，波动性更小，变化比较平稳
1.某“跑团”为了解团队每月跑步的平均里程，收集并整理了2021年1月至2021年11月期间“跑团”每月跑步的平均里程(单位：千米)的数据.绘制了下面的折线图.
解析　由折线图知，月跑步平均里程的中位数为5月份对应的平均里程数，A错误；月跑步平均里程不是逐月增加的，B错误；月跑步平均里程高峰期大致在9月和10月，C错误，故选D.
①0时到3时只进水不出水；②3时到4时不进水只出水；③4时到5时不进水也不出水.则一定正确的论断是________(填序号).
2.水池有两个相同的进水口和一个出水口，每个口进出水的速度如图甲、乙所示，某天0时到6时该水池的蓄水量如图丙所示，给出以下3个论断：
解析　由甲、乙、丙图可得进水速度为1，出水速度为2，结合丙图中直线的斜率可知，只进水不出水时，蓄水量增加的速度是2，故①正确；不进只出水时，蓄水量减少的速度为2，故②不正确；两个进水，一个出水时，蓄水量减少的速度也是0，故③不正确.
解析　由散点图的走势，知模型①不合适.
例1 我国在2020年进行了第七次人口普查登记，到2021年4月以后才能公布结果.人口增长可以用英国经济学家马尔萨斯提出的模型：y＝y0·ert，其中t表示经过的时间(单位：年)，y0表示t＝0时的人口数(单位：亿)，r表示人口的年平均增长率.以国家统计局发布的2000年第五次人口普查登记(已上报户口)的全国总人口12.43亿人(不包括香港、澳门和台湾地区)和2010年第六次人口普查登记(已上报户口)的全国总人口13.33亿人(不包括香港、澳门和台湾地区)为依据，用马尔萨斯人口增长模型估计我国2020年年末(不包括香港、澳门和台湾地区)的全国总人口数为(13.332＝177.688 9，12.432＝154.504 9)(　　)亿 亿亿 亿
所以我国2020年年末的全国总人口数约为
A.0.3 　　　　B.0.5C.0.7 　　　　D.0.8
训练1 我们检测视力时会发现对数视力表中有两列数据，分别是小数记录与五分记录，如图所示(已隐去数据)，其部分数据如下表：
解析　由题中数据可知，当x＝1时，y＝5，两个函数模型都符合；
所以选择模型y＝5＋lg x更合适，此时令y＝4.7，则lg x＝－0.3，所以x＝10－0.3≈0.5.
角度1　构造二次函数模型
整理得R2－12R＋32≤0，解得4≤R≤8，即R∈[4，8].
解析　设这种放射性物质最初的质量为1，经过x(x∈N)年后，剩余量是y，
则22x≥100，解得x≥4.所以至少需要的年数是4.
角度2　构造指数、对数函数模型
解析　设老师上课时声音强度、一般两人小声交谈时声音强度分别为x1 W/m2，x2 W/m2，
因此，老师上课时声音强度约为一般两人小声交谈时声音强度的10倍.
角度3　构建分段函数模型
解　每件产品售价为5元，则x万件产品的销售收入为5x万元.当0