




所属成套资源:备战2025年高考数学真题题源解密(新高考卷)
专题01 集合与常用逻辑用语(4大考向真题解读)-备战2025年高考数学真题题源解密(新高考卷)
展开
这是一份专题01 集合与常用逻辑用语(4大考向真题解读)-备战2025年高考数学真题题源解密(新高考卷),文件包含专题01集合与常用逻辑用语-2024年高考数学真题题源解密新高考卷原卷版docx、专题01集合与常用逻辑用语-2024年高考数学真题题源解密新高考卷解析版docx等2份试卷配套教学资源,其中试卷共25页, 欢迎下载使用。
命题分析
2024年高考新高考Ⅱ卷未考查集合,Ⅰ卷依旧考查了集合的交集运算,常用逻辑用语在新高考Ⅱ卷中考查了全称、存在量词命题真假的判断,这也说明了现在新高考“考无定题”,以前常考的现在不一定考了,抓住知识点和数学核心素养是关键!集合和常用逻辑用语考查应关注:(1)集合的基本运算和充要条件;(2)集合与简单的不等式、函数的定义域、值域的联系。预计2025年高考还是主要考查集合的基本运算。
试题精讲
1.(2024新高考Ⅰ卷·1)已知集合,则( )
A.B.C.D.
2.(2024新高考Ⅱ卷·2)已知命题p:,;命题q:,,则( )
A.p和q都是真命题B.和q都是真命题
C.p和都是真命题D.和都是真命题
1.(2022新高考Ⅰ卷·1)若集合,则( )
A.B.C.D.
2.(2023新高考Ⅰ卷·1)已知集合,,则( )
A.B.C.D.
3.(2022新高考Ⅱ卷·1)已知集合,则( )
A.B.C.D.
4.(2023新高考Ⅱ卷·2)设集合,,若,则( ).
A.2B.1C.D.
5.(2023新高考Ⅰ卷·7)记为数列的前项和,设甲:为等差数列;乙:为等差数列,则( )
A.甲是乙的充分条件但不是必要条件
B.甲是乙的必要条件但不是充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件也不是乙的必要条件
一、元素与集合
1、集合的含义与表示
某些指定对象的部分或全体构成一个集合.构成集合的元素除了常见的数、点等数学对象外,还可以是其他对象.
2、集合元素的特征
(1)确定性:集合中的元素必须是确定的,任何一个对象都能明确判断出它是否为该集合中的元素.
(2)互异性:集合中任何两个元素都是互不相同的,即相同元素在同一个集合中不能重复出现.
(3)无序性:集合与其组成元素的顺序无关.
3、元素与集合的关系
元素与集合之间的关系包括属于(记作)和不属于(记作)两种.
4、集合的常用表示法
集合的常用表示法有列举法、描述法、图示法(韦恩图).
5、常用数集的表示
二、集合间的基本关系
(1)子集:一般地,对于两个集合、,如果集合中任意一个元素都是集合中的元素,我们就说这两个集合有包含关系,称集合为集合的子集 ,记作(或),读作“包含于”(或“包含”).
(2)真子集:对于两个集合与,若,且存在,但,则集合是集合的真子集,记作(或).读作“真包含于 ”或“真包含 ”.
(3)相等:对于两个集合与,如果,同时,那么集合与相等,记作.
(4)空集:把不含任何元素的集合叫做空集,记作;是任何集合的子集,是任何非空集合的真子集.
三、集合的基本运算
(1)交集:由所有属于集合且属于集合的元素组成的集合,叫做与的交集,记作,即.
(2)并集:由所有属于集合或属于集合的元素组成的集合,叫做与的并集,记作,即.
(3)补集:对于一个集合,由全集中不属于集合的所有元素组成的集合称为集合相对于全集的补集,简称为集合的补集,记作,即.
四、集合的运算性质
(1),,,,.
(2),,,,.
(3),,.
(4)
【集合常用结论】
(1)若有限集中有个元素,则的子集有个,真子集有个,非空子集有个,非空真子集有个.
(2)空集是任何集合的子集,是任何非空集合的真子集.
(3).
(4),.
五、充分条件、必要条件、充要条件
1、定义
如果命题“若,则”为真(记作),则是的充分条件;同时是的必要条件.
2、从逻辑推理关系上看
(1)若且,则是的充分不必要条件;
(2)若且,则是的必要不充分条件;
(3)若且,则是的的充要条件(也说和等价);
(4)若且,则不是的充分条件,也不是的必要条件.
六、全称量词与存在量词
(1)全称量词与全称量词命题.短语“所有的”、“任意一个”在逻辑中通常叫做全称量词,并用符号“”表示.含有全称量词的命题叫做全称量词命题.全称量词命题“对中的任意一个,有成立”可用符号简记为“”,读作“对任意属于,有成立”.
(2)存在量词与存在量词命题.短语“存在一个”、“至少有一个”在逻辑中通常叫做存在量词,并用符号“”表示.含有存在量词的命题叫做存在量词命题.存在量词命题“存在中的一个,使成立”可用符号简记为“”,读作“存在中元素,使成立”(存在量词命题也叫存在性命题).
七、含有一个量词的命题的否定
(1)全称量词命题的否定为,.
(2)存在量词命题的否定为.
注:全称、存在量词命题的否定是高考常见考点之一.
【常用逻辑用语常用结论】
1、从集合与集合之间的关系上看
设.
(1)若,则是的充分条件(),是的必要条件;若,则是的充分不必要条件,是的必要不充分条件,即且;
注:关于数集间的充分必要条件满足:“小大”.
(2)若,则是的必要条件,是的充分条件;
(3)若,则与互为充要条件.
一、单选题
1.(2024·河南·三模)命题“”的否定是( )
A.B.
C.D.
2.(2024·湖南长沙·三模)已知集合,则( )
A.B.C.D.
3.(2024·河北衡水·三模)已知集合,则( )
A.B.C.D.
4.(2024·陕西·三模)已知集合,则( )
A.B.C.D.
5.(2024·安徽·三模)已知集合,,则图中所示的阴影部分的集合可以表示为( )
A.B.
C.D.
6.(2024·湖南长沙·三模)已知直线,圆,则“”是“直线上存在点,使点在圆内”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
7.(2024·湖北荆州·三模)已知集合,,其中是实数集,集合,则( )
A.B.C.D.
8.(2024·北京·三模)已知集合,若,则可能是( )
A.B.1C.2D.3
9.(2024·河北衡水·三模)已知函数,则“”是“函数是奇函数”的( )
A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
10.(2024·内蒙古·三模)设,是两个不同的平面,,是两条不同的直线,且则“”是“且”的( )
A.充分不必要条件B.充分必要条件
C.必要不充分条件D.既不充分也不必要条件
11.(2024·北京·三模)已知,,则( )
A.空集B.或
C.或且D.以上都不对
12.(2024·四川·三模)已知集合,,则( )
A.B.C.D.
13.(2024·重庆·三模)已知集合,则( )
A.B.C.D.
14.(2024·北京·三模)“为锐角三角形”是“,,”的( )
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件
15.(2024·上海·三模)设,集合,集合,对于集合B有下列两个结论:①存在a和b,使得集合B中恰有5个元素;②存在a和b,使得集合B中恰有4个元素.则下列判断正确的是( )
A.①②都正确B.①②都错误C.①错误,②正确D.①正确,②错误
二、多选题
16.(2024·江西南昌·三模)下列结论正确的是( )
A.若,则的取值范围是
B.若,则的取值范围是
C.若,则的取值范围是
D.若,则的取值范围是
17.(2024·辽宁·三模)已知表示这个数中最大的数.能说明命题“,,”是假命题的对应的一组整数a,b,c,d值的选项有( )
A.1,2,3,4B.,,7,5
C.8,,,D.5,3,0,
18.(2024·重庆·三模)命题“存在,使得”为真命题的一个充分不必要条件是( )
A.B.C.D.
19.(2024·黑龙江齐齐哈尔·三模)已知,则使得“”成立的一个充分条件可以是( )
A.B.C.D.
20.(2024·安徽安庆·三模)已知集合,集合,若有且仅有3个不同元素,则实数的值可以为( )
A.0B.1C.2D.3
三、填空题
21.(2024·湖南长沙·三模)已知集合,,若,则 .
22.(2024·上海·三模)已知集合,,则
23.(2024·湖南衡阳·三模)已知集合,集合,若,则 .
24.(2024·湖南邵阳·三模), ,则 .
25.(2024·安徽·三模)已知集合,若的所有元素之和为12,则实数 .
26.(2024·山东聊城·三模)已知集合,且,则实数的值为 .
27.(2024·重庆·三模)已知集合,,则满足B的集合的个数为 .
28.(2024·天津·三模)己知全集,集合,集合,则 , .
29.(2024·山东泰安·三模)已知集合,,若,则的取值范围是 .
30.(2024·宁夏银川·三模)已知命题p:关于x的方程有实根;命题q:关于x的函数在上单调递增,若“p或q”是真命题,“p且q”是假命题,则实数a的取值范围是 .
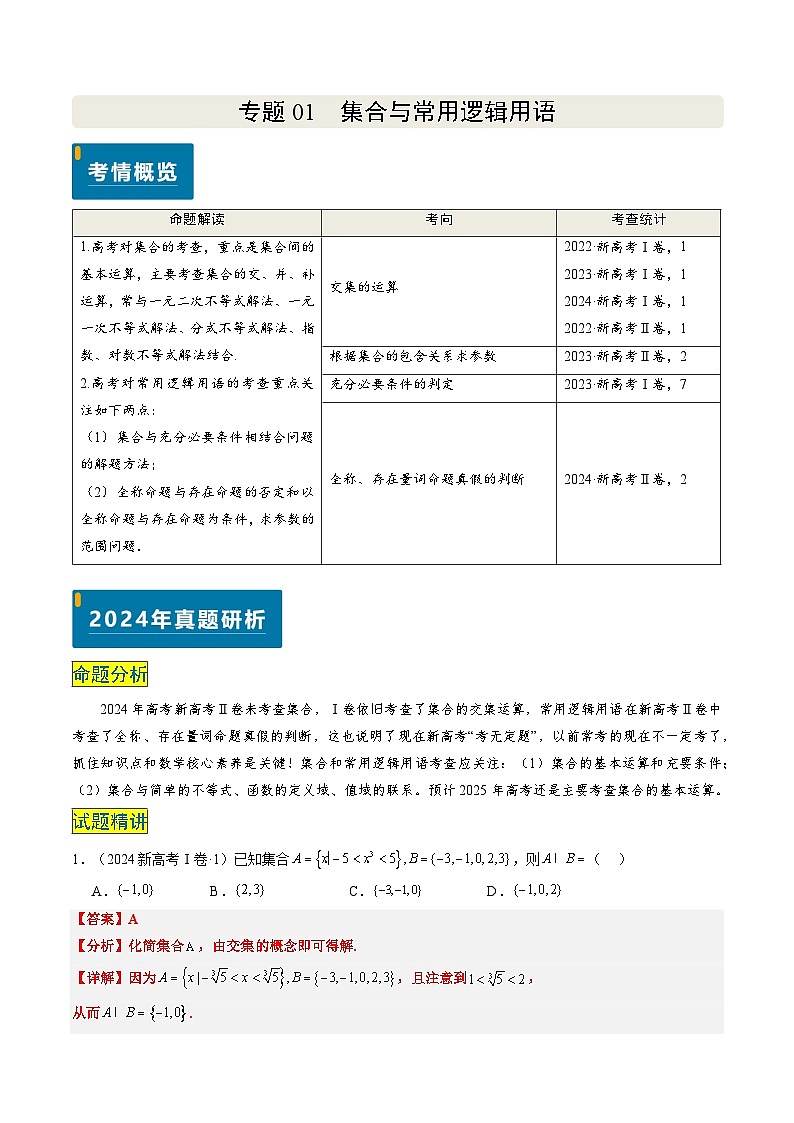
命题解读
考向
考查统计
1.高考对集合的考查,重点是集合间的基本运算,主要考查集合的交、并、补运算,常与一元二次不等式解法、一元一次不等式解法、分式不等式解法、指数、对数不等式解法结合.
2.高考对常用逻辑用语的考查重点关注如下两点:
(1)集合与充分必要条件相结合问题的解题方法;
(2)全称命题与存在命题的否定和以全称命题与存在命题为条件,求参数的范围问题.
交集的运算
2022·新高考Ⅰ卷,1
2023·新高考Ⅰ卷,1
2024·新高考Ⅰ卷,1
2022·新高考Ⅱ卷,1
根据集合的包含关系求参数
2023·新高考Ⅱ卷,2
充分必要条件的判定
2023·新高考Ⅰ卷,7
全称、存在量词命题真假的判断
2024·新高考Ⅱ卷,2
数集
自然数集
正整数集
整数集
有理数集
实数集
符号
或
相关试卷
这是一份专题13 数列(4大考向真题解读)-备战2025年高考数学真题题源解密(新高考卷),文件包含专题13数列4大考向真题解读--备战2025年高考数学真题题源解密新高考卷原卷版docx、专题13数列4大考向真题解读--备战2025年高考数学真题题源解密新高考卷解析版docx等2份试卷配套教学资源,其中试卷共54页, 欢迎下载使用。
这是一份专题11 概率(4大考向真题解读)-备战2025年高考数学真题题源解密(新高考卷),文件包含专题11概率4大考向真题解读--备战2025年高考数学真题题源解密新高考卷原卷版docx、专题11概率4大考向真题解读--备战2025年高考数学真题题源解密新高考卷解析版docx等2份试卷配套教学资源,其中试卷共65页, 欢迎下载使用。
这是一份专题10 统计(3大考向真题解读)-备战2025年高考数学真题题源解密(新高考卷),文件包含专题10统计3大考向真题解读--备战2025年高考数学真题题源解密新高考卷原卷版docx、专题10统计3大考向真题解读--备战2025年高考数学真题题源解密新高考卷解析版docx等2份试卷配套教学资源,其中试卷共45页, 欢迎下载使用。









