资料中包含下列文件,点击文件名可预览资料内容










还剩19页未读,
继续阅读
成套系列资料,整套一键下载
初中数学北师大版八年级上册1 为什么要证明教学ppt课件
展开
这是一份初中数学北师大版八年级上册1 为什么要证明教学ppt课件,文件包含北师大版数学八年级上册71为什么要证明课件pptx、71为什么要证明教案doc、71为什么要证明同步练习docx、71为什么要证明学案docx等4份课件配套教学资源,其中PPT共27页, 欢迎下载使用。
了解推理的意义,知道要判断一个数学结论是否正确,必须进行推理.
会用实验验证、举出反例、推理等方法简单地验证一个数学结论是否正确.
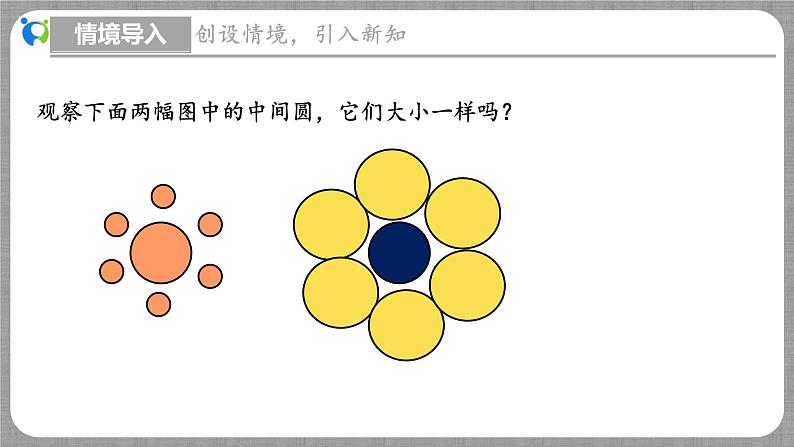
观察下面两幅图中的中间圆,它们大小一样吗?
线段AB和CD长度完全相等, 虽然它们看起来相差很大!
平行线:不敢相信图中的横线是平行的,不过它们就是平行线!
通过观察、度量、猜测得到的结论都正确吗?如果不是,那用什么方法才能说明它的正确性呢?
本章我们将一起学习如何根据一些基本事实推出其他结论的过程,证明与平行线的性质及判定有关的一些结论,证明三角形内角和定理,还将探讨三角形的内角与外角的关系.
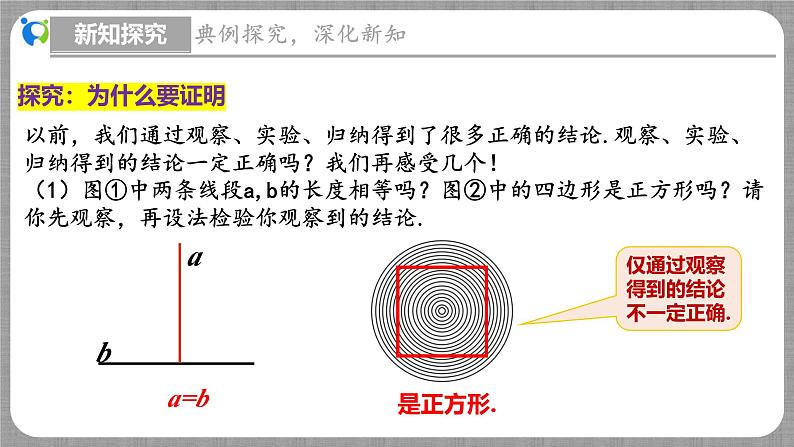
以前,我们通过观察、实验、归纳得到了很多正确的结论.观察、实验、归纳得到的结论一定正确吗?我们再感受几个!
仅通过观察得到的结论不一定正确.
所以它们的间隙不仅能放进一个红枣,而且也能放进一个拳头.
根据感觉经验得到的结论不一定正确!
(1)代数式n2-n+11的值是质数吗?取n=0,1,2,3,4,5试一试.你能否由此得到结论:对于所有的自然数n,式子n2-n+11的值都是质数吗?
答:当n=0,1,2,3,4,5时,n2-n+11的值分别是5,5,7,11,17,全是质数.而当n=11,时,n2-n+11=112-11+11=121=112.所以对于所有自然数,式子n2-n+11的值不都是质数.
根据不完全归纳得到的结论不一定正确.
这个故事告诉我们:1. 学习欧拉的求实精神与严谨的科学态度.
2.没有严格的推理,仅由若干特例归纳、猜测的结论可能潜藏着错误,未必正确.
3.要证明一个结论是错误的,举反例就是一种常用方法.
你能肯定你的结论对所有的△ABC都成立吗?与同伴交流.
根据测量得到的结论未必可信.
实验、观察、归纳得到的结论可能正确,也可能不正确.因此,要判断一个数学结论是否正确,仅仅依靠实验、观察、归纳是不够的,必须进行有根有据的证明.
解:观察可能得出的结论是:(1)实线是弯曲的;(2)a更长一些;(3)AB与DC不平行.而我们用科学的方法验证后发现:(1)实线是直的;(2)a与b一样长;(3)AB平行于CD.
例2:当n为正整数时,代数式(n2-5n+5)2的值都等于1吗?
解:当n=1时,(n2-5n+5)2=12=1;当n=2时,(n2-5n+5)2=(-1)2=1;当n=3时,(n2-5n+5)2=(-1)2=1;当n=4时,(n2-5n+5)2=12=1;当n=5时,(n2-5n+5)2=52=25≠1.所以当n为正整数时,(n2-5n+5)2不一定等于1.
【方法总结】验证特例是判断一个结论错误的最好方法.
解:(1)∵OA⊥OC,OB⊥OD,∴∠AOC=∠BOD=90°.∵∠BOC=30°,∴∠AOB=∠AOC-∠BOC=90°-30°=60°, ∠COD=∠BOD-∠BOC=90°-30°=60°.
(2)∠AOB=∠AOC-∠BOC=90°-54°=36°, ∠COD=∠BOD-∠BOC=90°-54°=36°.
(3)由(1)、(2)你发现了什么?(4)你能肯定上述的发现吗?
解:(3)由(1)(2)可发现:∠AOB=∠COD.
检验数学结论具体经历的过程是:观察、度量、实验→猜想归纳→结论→推理→正确结论.
检验数学结论的常用方法:实验验证、举出反例、推理证明.
2.下列说法中,①锐角都相等;②大于90°且小于平角的角是钝角;③互为相反数的两数和为0;④若l1⊥l2,l1⊥l3,则l2⊥l3.其中正确的有( )A.①② B.②③ C.③④ D.②④
3.下列结论中你能肯定的是( )A.今天下雨,明天必然还下雨B.三个连续整数的积一定能被6整除C.小明在数学竞赛中一定能获奖D.两张相片看起来佷像,则肯定照的是同一个人
4.下列问题用到推理的是( )A.根据a=10,b=10,得到a=bB.观察得到三角形有三个角C.老师告诉我们关于金字塔的许多奥秘D.由经验可知过两点有且只有一条直线
5.当n为正整数时,代数式(n2-5n+5)2的值都等于1吗?
解:当n=1时,(n2-5n+5)2=12=1;当n=2时,(n2-5n+5)2=(-1)2=1;当n=3时,(n2-5n+5)2=(-1)2=1;当n=4时,(n2-5n+5)2=12=1;当n=5时,(n2-5n+5)2=52=25≠1.所以当n为正整数时,(n2-5n+5)2不一定等于1.
检验数学结论的常用方法
检验数学结论具体经历的过程
1.下列推理正确的是( )A.弟弟今年13 岁,哥哥比弟弟大6岁到了明年,哥哥只比弟弟大 5 岁了B.如果 a>b,b>c,则 a>cC.∠A与∠B 相等,原因是它们看起来大小也差不多D.因为对顶角必然相等,所以相等的角也必是对顶角
2.某班有20位同学参加围棋、象棋比赛,甲说:“只参加一项的人数大于14.”乙说:“两项都参加的人数小于5.”对于甲、乙两人的说法,有下列四个说法中,其中正确的是( )A.若甲对,则乙对 C.若乙错,则甲错B.若乙对,则甲对 D.若甲错,则乙对
3.甲、乙、丙三人进行乒乓球比赛,规则是:两人比赛,另一人当裁判,输者将在下一局中担任裁判,每一局比赛没有平局.已知甲、乙各比赛了4局,丙当了3次裁判.则第二局的输者是( )A.甲 B.乙 C.丙 D.丁
4.当n为正整数时,n2+3n+1的值一定是质数吗?
解:不是,当n=6时, n2+3n+1=55不是质数。
5.观察下列等式:12×231 = 132×21,13×341 = 143×31,23×352 =253×32,34×473 = 374×43,62×286 =682×26,…以上等式中两边数字是对称的,且每个等式中组成两位数与三位数的数字之间具有相同的规律,我们称这类等式为“数字对称等式”.(1)根据上述各式反映的规律填空,使式子成为“数字对称等式”:①52× = ×25;② ×396=693× .(2)设这类等式左边两位数的十位数字为 a,个位数字为b,且2≤a+b≤9,写出表示“数字对称等式”一般规律的式子(含a,b),并写出推理过程.
(2)(10a+b)·[100b+10(a+b)+a]=[100a+10(a+b)+b]·(10b+a).推理过程:左边=(10a+b)(110b+11a)= 11 (10a+b)(10b+a),右边=(110a+11b)(10b+a)= 11 (10a+b)(10b+a),左边=右边,即所列等式成立.
教材习题7.1.
了解推理的意义,知道要判断一个数学结论是否正确,必须进行推理.
会用实验验证、举出反例、推理等方法简单地验证一个数学结论是否正确.
观察下面两幅图中的中间圆,它们大小一样吗?
线段AB和CD长度完全相等, 虽然它们看起来相差很大!
平行线:不敢相信图中的横线是平行的,不过它们就是平行线!
通过观察、度量、猜测得到的结论都正确吗?如果不是,那用什么方法才能说明它的正确性呢?
本章我们将一起学习如何根据一些基本事实推出其他结论的过程,证明与平行线的性质及判定有关的一些结论,证明三角形内角和定理,还将探讨三角形的内角与外角的关系.
以前,我们通过观察、实验、归纳得到了很多正确的结论.观察、实验、归纳得到的结论一定正确吗?我们再感受几个!
仅通过观察得到的结论不一定正确.
所以它们的间隙不仅能放进一个红枣,而且也能放进一个拳头.
根据感觉经验得到的结论不一定正确!
(1)代数式n2-n+11的值是质数吗?取n=0,1,2,3,4,5试一试.你能否由此得到结论:对于所有的自然数n,式子n2-n+11的值都是质数吗?
答:当n=0,1,2,3,4,5时,n2-n+11的值分别是5,5,7,11,17,全是质数.而当n=11,时,n2-n+11=112-11+11=121=112.所以对于所有自然数,式子n2-n+11的值不都是质数.
根据不完全归纳得到的结论不一定正确.
这个故事告诉我们:1. 学习欧拉的求实精神与严谨的科学态度.
2.没有严格的推理,仅由若干特例归纳、猜测的结论可能潜藏着错误,未必正确.
3.要证明一个结论是错误的,举反例就是一种常用方法.
你能肯定你的结论对所有的△ABC都成立吗?与同伴交流.
根据测量得到的结论未必可信.
实验、观察、归纳得到的结论可能正确,也可能不正确.因此,要判断一个数学结论是否正确,仅仅依靠实验、观察、归纳是不够的,必须进行有根有据的证明.
解:观察可能得出的结论是:(1)实线是弯曲的;(2)a更长一些;(3)AB与DC不平行.而我们用科学的方法验证后发现:(1)实线是直的;(2)a与b一样长;(3)AB平行于CD.
例2:当n为正整数时,代数式(n2-5n+5)2的值都等于1吗?
解:当n=1时,(n2-5n+5)2=12=1;当n=2时,(n2-5n+5)2=(-1)2=1;当n=3时,(n2-5n+5)2=(-1)2=1;当n=4时,(n2-5n+5)2=12=1;当n=5时,(n2-5n+5)2=52=25≠1.所以当n为正整数时,(n2-5n+5)2不一定等于1.
【方法总结】验证特例是判断一个结论错误的最好方法.
解:(1)∵OA⊥OC,OB⊥OD,∴∠AOC=∠BOD=90°.∵∠BOC=30°,∴∠AOB=∠AOC-∠BOC=90°-30°=60°, ∠COD=∠BOD-∠BOC=90°-30°=60°.
(2)∠AOB=∠AOC-∠BOC=90°-54°=36°, ∠COD=∠BOD-∠BOC=90°-54°=36°.
(3)由(1)、(2)你发现了什么?(4)你能肯定上述的发现吗?
解:(3)由(1)(2)可发现:∠AOB=∠COD.
检验数学结论具体经历的过程是:观察、度量、实验→猜想归纳→结论→推理→正确结论.
检验数学结论的常用方法:实验验证、举出反例、推理证明.
2.下列说法中,①锐角都相等;②大于90°且小于平角的角是钝角;③互为相反数的两数和为0;④若l1⊥l2,l1⊥l3,则l2⊥l3.其中正确的有( )A.①② B.②③ C.③④ D.②④
3.下列结论中你能肯定的是( )A.今天下雨,明天必然还下雨B.三个连续整数的积一定能被6整除C.小明在数学竞赛中一定能获奖D.两张相片看起来佷像,则肯定照的是同一个人
4.下列问题用到推理的是( )A.根据a=10,b=10,得到a=bB.观察得到三角形有三个角C.老师告诉我们关于金字塔的许多奥秘D.由经验可知过两点有且只有一条直线
5.当n为正整数时,代数式(n2-5n+5)2的值都等于1吗?
解:当n=1时,(n2-5n+5)2=12=1;当n=2时,(n2-5n+5)2=(-1)2=1;当n=3时,(n2-5n+5)2=(-1)2=1;当n=4时,(n2-5n+5)2=12=1;当n=5时,(n2-5n+5)2=52=25≠1.所以当n为正整数时,(n2-5n+5)2不一定等于1.
检验数学结论的常用方法
检验数学结论具体经历的过程
1.下列推理正确的是( )A.弟弟今年13 岁,哥哥比弟弟大6岁到了明年,哥哥只比弟弟大 5 岁了B.如果 a>b,b>c,则 a>cC.∠A与∠B 相等,原因是它们看起来大小也差不多D.因为对顶角必然相等,所以相等的角也必是对顶角
2.某班有20位同学参加围棋、象棋比赛,甲说:“只参加一项的人数大于14.”乙说:“两项都参加的人数小于5.”对于甲、乙两人的说法,有下列四个说法中,其中正确的是( )A.若甲对,则乙对 C.若乙错,则甲错B.若乙对,则甲对 D.若甲错,则乙对
3.甲、乙、丙三人进行乒乓球比赛,规则是:两人比赛,另一人当裁判,输者将在下一局中担任裁判,每一局比赛没有平局.已知甲、乙各比赛了4局,丙当了3次裁判.则第二局的输者是( )A.甲 B.乙 C.丙 D.丁
4.当n为正整数时,n2+3n+1的值一定是质数吗?
解:不是,当n=6时, n2+3n+1=55不是质数。
5.观察下列等式:12×231 = 132×21,13×341 = 143×31,23×352 =253×32,34×473 = 374×43,62×286 =682×26,…以上等式中两边数字是对称的,且每个等式中组成两位数与三位数的数字之间具有相同的规律,我们称这类等式为“数字对称等式”.(1)根据上述各式反映的规律填空,使式子成为“数字对称等式”:①52× = ×25;② ×396=693× .(2)设这类等式左边两位数的十位数字为 a,个位数字为b,且2≤a+b≤9,写出表示“数字对称等式”一般规律的式子(含a,b),并写出推理过程.
(2)(10a+b)·[100b+10(a+b)+a]=[100a+10(a+b)+b]·(10b+a).推理过程:左边=(10a+b)(110b+11a)= 11 (10a+b)(10b+a),右边=(110a+11b)(10b+a)= 11 (10a+b)(10b+a),左边=右边,即所列等式成立.
教材习题7.1.














