






2025版高考数学全程一轮复习第二章函数第三节函数的奇偶性周期性课件
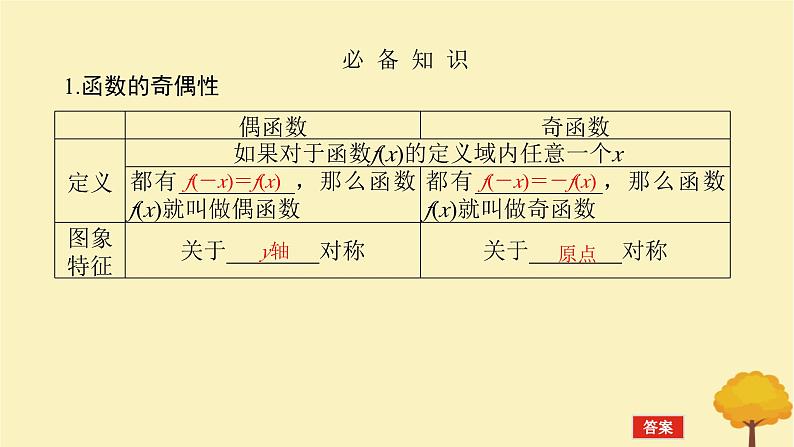
展开必 备 知 识1.函数的奇偶性
f(-x)=-f(x)
2.函数的周期性(1)周期函数:对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的任何值时,都有___________,那么就称函数f(x)为周期函数,称T为这个函数的周期.(2)最小正周期:如果在周期函数f(x)的所有周期中存在一个___________,那么这个_________就叫做f(x)的最小正周期.
f(x+T)=f(x)
【常用结论】1.函数奇偶性的五个重要结论(1)如果一个奇函数f(x)在x=0处有意义,即f(0)有意义,那么一定有f(0)=0.(2)如果函数f(x)是偶函数,那么f(x)=f(|x|).(3)奇函数在关于原点对称的区间上具有相同的单调性;偶函数在关于原点对称的区间上具有相反的单调性.(4)在公共定义域内有:奇±奇=奇,偶±偶=偶,奇×奇=偶,偶×偶=偶,奇×偶=奇.(5)只有f(x)=0(定义域是关于原点对称的非空数集)既是奇函数又是偶函数.
夯 实 基 础1.思考辨析(正确的打“√”,错误的打“×”)(1)函数y=x2在x∈(0,+∞)时是偶函数.( )(2)若函数f(x)为奇函数,则一定有f(0)=0.( )(3)不存在既是奇函数,又是偶函数的函数.( )(4)若T是函数的一个周期,则nT(n∈Z,n≠0)也是函数的周期.( )
解析:由奇函数的定义可知BC为奇函数.故选BC.
3.(教材改编)设奇函数f(x)的定义域为[-5,5],若当x∈[0,5]时,f(x)的图象如图所示,则不等式f(x)<0的解集是_______________.
5.(易错)已知函数f(x)是定义域为R的奇函数,当x≥0时,f(x)=x(1+x),则f(x)的解析式为___________________.
解析:当x<0时,则-x>0,∴f(-x)=(-x)(1-x)=-x(1-x),又f(x)为奇函数,∴f(-x)=-f(x),∴-f(x)=-x(1-x),即f(x)=x(1-x).
1.了解函数奇偶性的含义,了解函数的周期性及其几何意义.2.会依据函数的性质进行简单的应用.
问题思考·夯实技能【问题1】 “a+b=0”是“函数f(x)在区间[a,b](a≠b)上具有奇偶性”的什么条件?请说明理由.
提示:必要不充分条件因为偶函数的图象关于y轴对称,奇函数的图象关于原点对称.
题后师说判断函数奇偶性的方法
(2)已知函数f(x)是定义在R上的偶函数,且当x≥0时,f(x)=-x2+3x,则f(x)的解析式为____________________.
题后师说(1)求参数:根据f(-x)±f(x)=0得到关于待求参数的恒等式,再求出参数的值.在解答选择题、填空题时,一般选用特值法,如函数f(x)为奇函数(在x=0处有定义),则用f(0)=0求解等.(2)求解析式(或函数值):将待求区间上的自变量转化到已知区间上,再利用奇偶性求出.
(2)已知函数f(x)是定义在[-1,1]上的奇函数,当0
题后师说利用奇偶性可画出另一对称区间上的函数图象及判断另一区间上函数的单调性.
题型三 函数的周期性例4 [2024·山西晋中模拟]设f(x)是定义在R上的奇函数,且对任意实数x,恒有f(x+2)=-f(x),当x∈[0,2]时,f(x)=2x-x2.(1)求证:f(x)是周期函数;(2)当x∈[2,4]时,求f(x)的解析式;(3)计算f(0)+f(1)+f(2)+…+f(2 023).
解析:(1)证明:f(x+2)=-f(x)⇒f(x+2+2)=-f(x+2)⇒f(x+4)=f(x),所以f(x)是以4为周期的周期函数.(2)当x∈[-2,0]时,因为函数f(x)是定义在R上的奇函数,所以f(x)=-f(-x)=-[2(-x)-(-x)2]=x2+2x,当x∈[2,4]时,f(x)=f(x-4)=(x-4)2+2(x-4)=x2-6x+8.(3)f(0)=0,f(1)=1,f(2)=0,f(3)=-1,因为函数f(x)的周期为4,所以f(0)+f(1)+f(2)+…+f(2 023)=506×[f(0)+f(1)+f(2)+f(3)]=0.
题后师说(1)求解与函数的周期有关的问题,应根据题目特征及周期定义,求出函数的周期.(2)利用函数的周期性,可将其他区间上的求值,求零点个数、求解析式等问题,转化到已知区间上,进而解决问题.
1.[2023·安徽合肥模拟]已知函数f(x)为R上的奇函数,当x≥0时,f(x)=ex+x+m,则f(-1)=( )A.e B.-eC.e+1 D.-e-1
解析:函数f(x)为R上的奇函数,则f(0)=e0+0+m=0,解得m=-1,f(-1)=-f(1)=-(e+1-1)=-e.
2.已知定义在R上的函数f(x)满足f(x+2)=-f(x),且当x∈[0,2)时,f(x)=lg2(x+1),则f(47)=( )A.2 B.0C.1 D.-1
解析:由f(x+2)=-f(x)得f(x+4)=-f(x+2),所以f(x)=f(x+4),所以函数f(x)的周期为4,所以f(47)=f(4×12-1)=f(-1),因为f(x)=-f(x+2),所以f(-1)=-f(1)=-lg22=-1.
4.[2023·河北邯郸一模]已知函数f(x-1)为偶函数,且函数f(x)在[-1,+∞)上单调递增,则关于x的不等式f(1-2x)
2024版新教材高考数学全程一轮总复习第二章函数与基本初等函数第三节函数的奇偶性周期性与对称性课件: 这是一份2024版新教材高考数学全程一轮总复习第二章函数与基本初等函数第三节函数的奇偶性周期性与对称性课件,共60页。PPT课件主要包含了必备知识·夯实双基,关键能力·题型突破,f-x=fx,最小的正数,最小正数,答案BC,答案D,答案BD,答案C,答案A等内容,欢迎下载使用。
高考数学一轮复习配套课件 第二章 第三节 函数的奇偶性与周期性: 这是一份高考数学一轮复习配套课件 第二章 第三节 函数的奇偶性与周期性,共59页。PPT课件主要包含了必备知识基础落实,关键能力考点突破,微专题,任意一个,f-x=fx,存在一个最小,最小正数,答案D,答案B,答案A等内容,欢迎下载使用。
新课标2022版高考数学总复习第二章函数第三节函数的奇偶性与周期性课件文: 这是一份新课标2022版高考数学总复习第二章函数第三节函数的奇偶性与周期性课件文,共60页。












