



2025版高考数学全程一轮复习第四章三角函数与解三角形第八节正弦余弦定理应用举例课件
展开
这是一份2025版高考数学全程一轮复习第四章三角函数与解三角形第八节正弦余弦定理应用举例课件,共38页。PPT课件主要包含了课前自主预习案,课堂互动探究案,答案B,答案A,答案C等内容,欢迎下载使用。
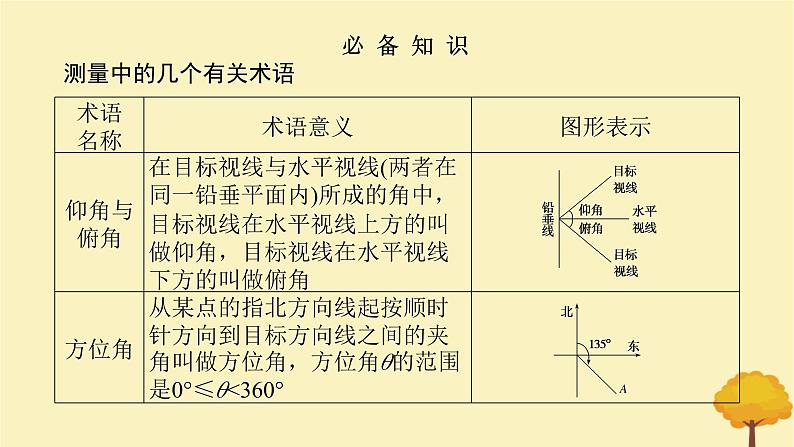
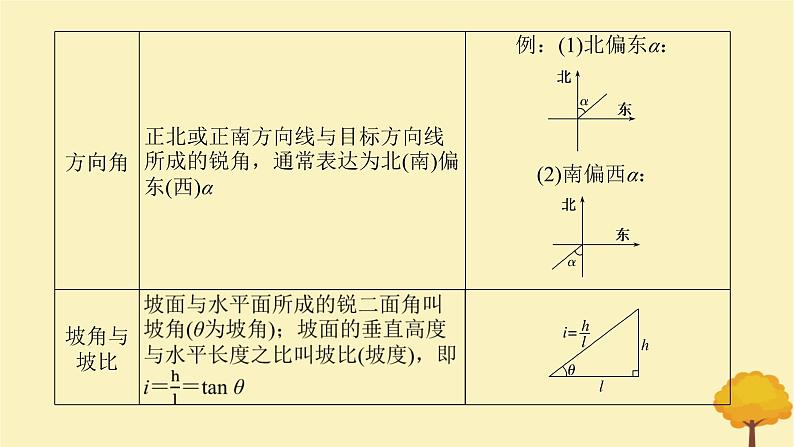
必 备 知 识测量中的几个有关术语
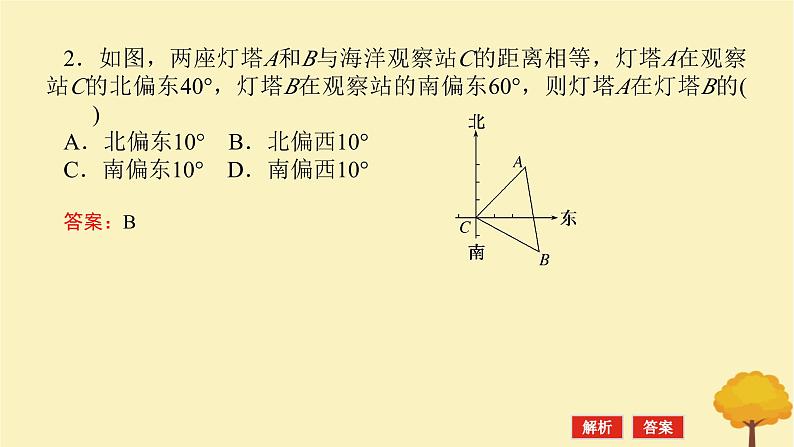
2.如图,两座灯塔A和B与海洋观察站C的距离相等,灯塔A在观察站C的北偏东40°,灯塔B在观察站的南偏东60°,则灯塔A在灯塔B的( )A.北偏东10° B.北偏西10°C.南偏东10° D.南偏西10°
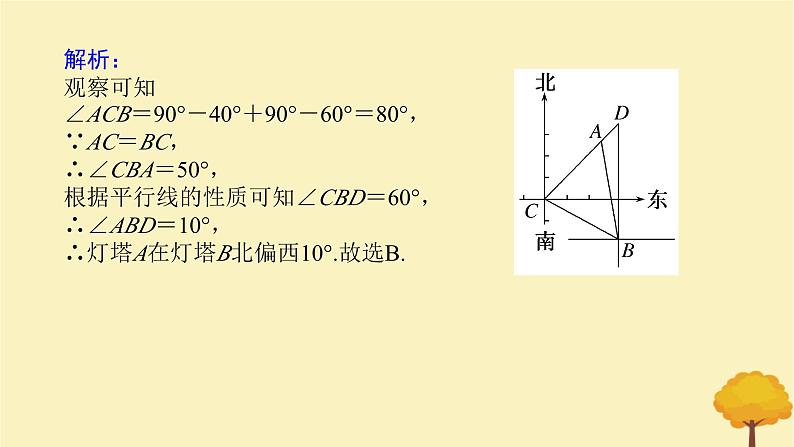
解析:观察可知∠ACB=90°-40°+90°-60°=80°,∵AC=BC,∴∠CBA=50°,根据平行线的性质可知∠CBD=60°,∴∠ABD=10°,∴灯塔A在灯塔B北偏西10°.故选B.
3.如图所示,D,C,B三点在地面的同一直线上,DC=a,从点C,D测得点A的仰角分别为60°,30°,则A点离地面的高度AB=________.
会运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.
关键能力·题型剖析题型一 测量距离问题例 1 [2024·广东广州模拟]海洋蓝洞是地球罕见的自然地理现象,被喻为“地球留给人类保留宇宙秘密的最后遗产”,我国拥有世界上最深的海洋蓝洞,若要测量如图所示的蓝洞的口径A,B两点间的距离,现在珊瑚群岛上取两点C,D,测得CD=35 m,∠ADB=135°,∠BDC=∠DCA=15°,∠ACB=120°,则A、B两点的距离为________ m.
题后师说测量距离问题的求解策略
题后师说测量高度问题的三个注意点(1)要理解仰角、俯角、方向(位)角的概念.(2)在实际问题中,若遇到空间与平面(地面)同时研究的问题,最好画两个图形,一个空间图形,一个平面图形.(3)注意山或塔垂直于地面或海平面,把空间问题转化为平面问题.
(1)当走私船发现了巡逻艇时,两船相距多少海里;
(2)问巡逻艇应该沿什么方向去追,才能最快追上走私船.
题后师说角度问题的解题方法首先应明确方向角的含义,在解应用题时,分析题意,分清已知与所求,再根据题意正确画出示意图,这是最关键、最重要的一步,通过这一步可将实际问题转化成可用数学方法解决的问题,解题中也要注意体会正、余弦定理“联袂”使用的优点.
3.[2024·山西太原模拟]某海轮以30海里/时的速度航行,在点A测得海面上油井P在南偏东60°方向上,向北航行40分钟后到达点B,测得油井P在点B的南偏东30°方向上,海轮改为北偏东60°的航向再行驶80分钟到达点C,则P、C间的距离为________海里.
相关课件
这是一份2024版新教材高考数学全程一轮总复习高考大题研究课四利用正弦余弦定理解三角形课件,共33页。
这是一份2024版新教材高考数学全程一轮总复习第四章三角函数与解三角形第七节正弦定理余弦定理课件,共37页。PPT课件主要包含了必备知识·夯实双基,关键能力·题型突破,RsinB,RsinC,答案C,答案D,答案A,答案B,等腰或直角三角形等内容,欢迎下载使用。
这是一份2024版新教材高考数学全程一轮总复习第四章三角函数与解三角形第八节正弦余弦定理应用举例课件,共28页。PPT课件主要包含了必备知识·夯实双基,关键能力·题型突破,水平视线,正北方向,水平角,答案B,答案C,答案A等内容,欢迎下载使用。









