2025版高考数学全程一轮复习第四章三角函数与解三角形第五节三角函数的图象与性质课件

这是一份2025版高考数学全程一轮复习第四章三角函数与解三角形第五节三角函数的图象与性质课件，共49页。PPT课件主要包含了课前自主预习案，课堂互动探究案，π－1，－11，奇函数，偶函数，kπ0，x＝kπ，答案B，答案π等内容，欢迎下载使用。

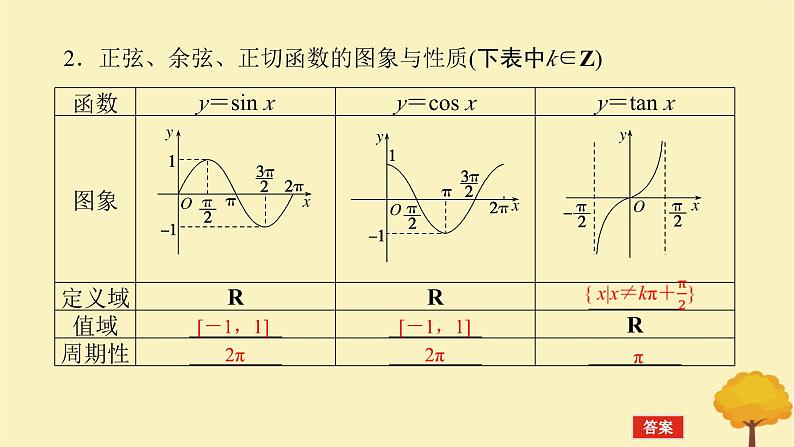
2．正弦、余弦、正切函数的图象与性质(下表中k∈Z)
[－π＋2kπ，2kπ]
[2kπ，π＋2kπ]
夯 实 基 础　1．思考辨析(正确的打“√”，错误的打“×”)(1)y＝sin x在第一象限是增函数．(　　)(2)正切函数y＝tan x在定义域内是增函数．(　　)(3)已知y＝k sin x＋1，x∈R，则y的最大值为k＋1.(　　)(4)y＝sin |x|是偶函数．(　　)
4．(易错)函数y＝|sin x|的最小正周期为________．
解析：函数y＝|sin x|的最小正周期是函数y＝sin x的周期的一半，故函数y＝|sin x|的最小正周期是π.
问题思考·夯实技能【问题1】　终边相同的角的三角函数值有什么关系？这个关系式体现了三角函数的什么性质？
提示：终边相同的角的三角函数值相等，即sin (2kπ＋x)＝sin x(k∈Z)，cs (2kπ＋x)＝cs x(k∈Z)，这个公式体现了三角函数的周期性．
【问题2】　函数y＝A sin (ωx＋φ)，y＝A cs (ωx＋φ)的奇偶性与φ的取值的关系是怎样的？
关键能力·题型剖析题型一 三角函数的定义域和值域(或最值)例 1 (1)函数y＝lg (cs x－sin x)的定义域是______________________.
题后师说求解三角函数的值域(最值)的3种方法
(3)函数y＝sin x－cs2x的值域为________．
题后师说(1)三角函数中奇函数一般可化为y＝A sin ωx或y＝A tan ωx的形式，而偶函数一般可化为y＝A cs ωx的形式．(2)求三角函数图象的所有对称轴方程或对称中心坐标时，可利用整体换元方法进行求解，注意熟记正弦型、余弦型函数图象对称轴方程、对称中心横坐标的公式．
【变式练习】　本例条件不变，求在[0，π]上的单调递减区间．
题后师说求形如y＝A sin (ωx＋φ)或y＝A cs (ωx＋φ)(其中ω>0)的单调区间时，要视“ωx＋φ”为一个整体，通过解不等式求解．但如果ω<0，可先借助诱导公式将ω化为正数，防止把单调性弄错．
题后师说求出原函数的相应单调区间，由已知区间是所求某区间的子集，列不等式(组)求解．