2025版高考数学全程一轮复习第五章平面向量与复数第三节平面向量的数量积及其应用课件

这是一份2025版高考数学全程一轮复习第五章平面向量与复数第三节平面向量的数量积及其应用课件，共51页。PPT课件主要包含了课前自主预习案，课堂互动探究案，a⊥b，投影向量，acosθ·e，a·c＋b·c，x1x2＋y1y2，答案A，答案钝角，答案D等内容，欢迎下载使用。

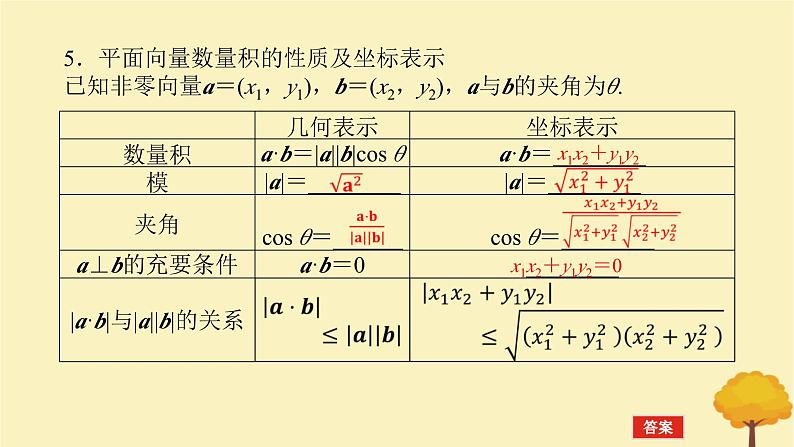
5．平面向量数量积的性质及坐标表示已知非零向量a＝(x1，y1)，b＝(x2，y2)，a与b的夹角为θ.
x1x2＋y1y2＝0
【常用结论】1．平面向量数量积运算的常用公式(1)(a＋b)·(a－b)＝a2－b2.(2)(a±b)2＝a2±2a·b＋b2.2．有关向量夹角的两个结论(1)若两个向量a与b的夹角为锐角，则有a·b＞0，反之不成立(因为a与b的夹角为0时不成立)．(2)若两个向量a与b的夹角为钝角，则有a·b＜0，反之不成立(因为a与b的夹角为π时不成立)．
夯 实 基 础　1．思考辨析(正确的打“√”，错误的打“×”)(1)两向量的数量积是一个向量．(　　)(2)一个向量在另一个向量方向上的投影为数量，而不是向量．(　　)(3)(a·b)·c＝a·(b·c)．(　　)(4)若a·b＝a·c(a≠0)，则b＝c.(　　)
3．(教材改编)已知平面向量a＝(2，－1)，b＝(m，2)，且a⊥b，则|a＋b|＝________．
5．(易错)设向量a＝(x，－4)，b＝(1，－x)，向量a与b的夹角为锐角，则x的取值范围为________．
1.理解平面向量数量积的含义及其几何意义．2．了解平面向量的数量积与投影向量的关系．3．掌握数量积的坐标表达式，会进行平面向量数量积的运算．4．能用数量积表示两个向量的夹角，会用数量积判断两个平面向量的垂直关系．5．会用向量方法解决简单的平面几何问题．
问题思考·夯实技能　【问题1】　两个向量的数量积大于0(或小于0)，则夹角一定为锐角(或钝角)吗？
提示：不一定．当两个向量的夹角为0(或π)时，数量积也大于0(或小于0)．
【问题2】　由a·b＝0一定可以得出a＝0或b＝0吗？
提示：不能推出a＝0或b＝0.因为当a·b＝0时，还有可能a⊥b.
题后师说平面向量数量积运算的3种策略
角度二　向量的夹角例 3 [2024·安徽亳州模拟]已知非零向量a，b，c满足|a|＝1，(a－b)·(a＋b)＝－1，a·b＝1，c＝－2b.则向量a与c的夹角为(　　)A．45° B．60°C．135° D．150°
解析：由已知得2a＋b＝2(m＋1，m－1)＋(－1，m)＝(2m＋1，3m－2)，∵(2a＋b)⊥c，且c＝(－1，1)，∴(2a＋b)·c＝－(2m＋1)＋3m－2＝0，解得m＝3.故选B.
巩固训练2(1)(多选)[2024·广东广州模拟]已知向量a＝(1，2)，b＝(－2，1)，则(　　)A．(a－b)⊥(a＋b)B．(a－b)∥(a＋b)C．|a－b|＝|a＋b|D．b－a在a上的投影向量是a
题后师说平面向量的综合应用主要是利用平面向量的知识作为解题工具，解决平面几何问题、三角函数问题、解三角形问题、解析几何问题、实际问题等．
(2)一条河宽为800 m，一艘船从岸边的某处出发向对岸航行．船的速度的大小为20 km/h，水流速度的大小为12 km/h，则当航程最短时，这艘船行驶完全程所需要的时间为________ min.
1．[2023·新课标Ⅰ卷]已知向量a＝(1，1)，b＝(1，－1)，若(a＋λb)⊥(a＋μb)，则(　　)A．λ＋μ＝1 B．λ＋μ＝－1C．λμ＝1 D．λμ＝－1
解析：因为a＝(1，1)，b＝(1，－1)，所以a＋λb＝(1＋λ，1－λ)，a＋μb＝(1＋μ，1－μ)，由(a＋λb)⊥(a＋μb)可得，(a＋λb)·(a＋μb)＝0，即(1＋λ)(1＋μ)＋(1－λ)(1－μ)＝0，整理得：λμ＝－1.故选D.