






2025版高考数学全程一轮复习第一章集合与常用逻辑用语不等式第五节二次函数与一元二次方程不等式课件
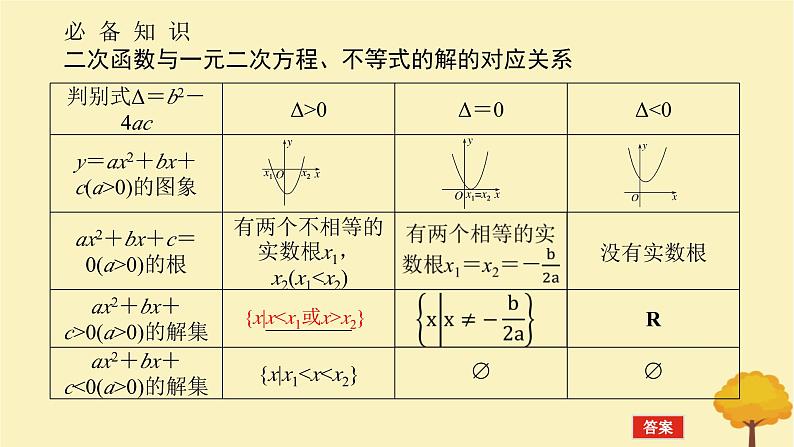
展开必 备 知 识二次函数与一元二次方程、不等式的解的对应关系
{x|x
夯 实 基 础1.思考辨析(正确的打“√”,错误的打“×”)(1)若不等式ax2+bx+c<0的解集为(x1,x2),则必有a>0.( )(2)若方程ax2+bx+c=0(a≠0)没有实数根,则不等式ax2+bx+c>0的解集为R.( )(3)不等式ax2+bx+c≥0在R上恒成立的条件是a>0且Δ=b2-4ac≤0.( )(4)若二次函数y=ax2+bx+c的图象开口向下,则不等式ax2+bx+c<0的解集一定不是空集.( )
3.(教材改编)已知关于x的不等式x2-ax-b<0的解集是(2,3),则a+b的值是________.
解析:若关于x的不等式x2-ax-b<0的解集是(2,3),则2,3是方程x2-ax-b=0的根,故a=5,b=-6,故a+b=-1.
5.(易错)要使函数y=mx2+mx+m-1的值恒为负值,则m的取值范围为________.
1.会结合一元二次函数的图象,判断一元二次方程实根的存在性及实根的个数.2.能借助一元二次函数求解一元二次不等式.3.了解简单的分式不等式、绝对值不等式的解法.
问题思考·夯实技能【问题1】 一元二次不等式的解集与一元二次方程的根的关系是什么?
【问题2】 不等式ax2+bx+c>0(≥0),ax2+bx+c<0(≤0)在R上恒成立的条件分别是什么?
关键能力·题型剖析题型一 一元二次不等式的解法角度一 不含参数的一元二次不等式的解法例 1 解下列不等式:(1)-x2+4x+5<0;(2)2x2-5x+2≤0.
题后师说解一元二次不等式的一般步骤
角度二 含参数的一元二次不等式的解法例 2 解关于x的不等式ax2-(a+1)x+1<0(a>0).
【变式练习】 把本例中的条件“a>0”改为“a∈R”,不等式的解集如何?
题后师说解含参数的一元二次不等式,要把握好分类讨论的层次,一般按下面次序进行讨论:首先根据二次项系数的符号进行分类,其次根据根是否存在,即Δ的符号进行分类,最后在根存在时,根据根的大小进行分类.
巩固训练2解关于x的不等式12x2-ax>a2.
题后师说给出一元二次不等式的解集,相当于知道了相应二次函数的开口方向及与x轴的交点,可以利用代入根或根与系数的关系求待定系数.
角度二 在给定区间上恒成立问题例 6 已知f(x)=x2+ax+3-a,若x∈[-2,2]时,f(x)≥0恒成立,则实数a的取值范围为________.
角度三 在给定参数范围内的恒成立问题例 7 已知a∈[-1,1],不等式x2+(a-4)x+4-2a>0恒成立,则x的取值范围为__________.
题后师说恒成立问题求参数的范围的解题策略
巩固训练5(1)若不等式kx2-2x+6k<0(k≠0)的解集为R,则k的取值范围为________.
(2)若不等式x2+ax+4≥0对一切x∈[1,3]恒成立,则a的最小值为________.
(3)函数f(x)=x2+ax+3,若a∈[4,6],f(x)≥0恒成立,则实数x的取值范围是__________.
2.已知不等式x2+ax+4<0的解集为空集,则实数a的取值范围是( )A.{a|a≤-4或a≥4} B.{a|-4≤a≤4}C.{a|a<-4或a>4} D.{a|-4
2025版高考数学全程一轮复习第一章集合与常用逻辑用语不等式第三节等式性质与不等式性质课件: 这是一份2025版高考数学全程一轮复习第一章集合与常用逻辑用语不等式第三节等式性质与不等式性质课件,共37页。PPT课件主要包含了课前自主预习案,课堂互动探究案,不等式的性质,acbc,acbd,答案A,答案ab,答案D,答案-65,答案B等内容,欢迎下载使用。
2025版高考数学全程一轮复习第一章集合与常用逻辑用语不等式第一节集合课件: 这是一份2025版高考数学全程一轮复习第一章集合与常用逻辑用语不等式第一节集合课件,共46页。PPT课件主要包含了课前自主预习案,课堂互动探究案,确定性,无序性,互异性,列举法,描述法,N或N+,集合间的基本关系,任意一个元素等内容,欢迎下载使用。
2025版高考数学全程一轮复习第一章集合与常用逻辑用语不等式第四节基本不等式课件: 这是一份2025版高考数学全程一轮复习第一章集合与常用逻辑用语不等式第四节基本不等式课件,共49页。PPT课件主要包含了课前自主预习案,课堂互动探究案,a0b0,a=b,x=y,常用结论,答案B,答案25,答案C,答案D等内容,欢迎下载使用。












