还剩14页未读，
继续阅读
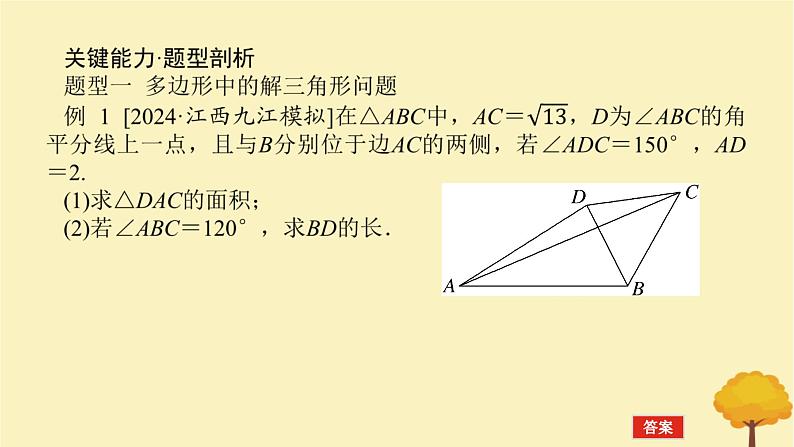
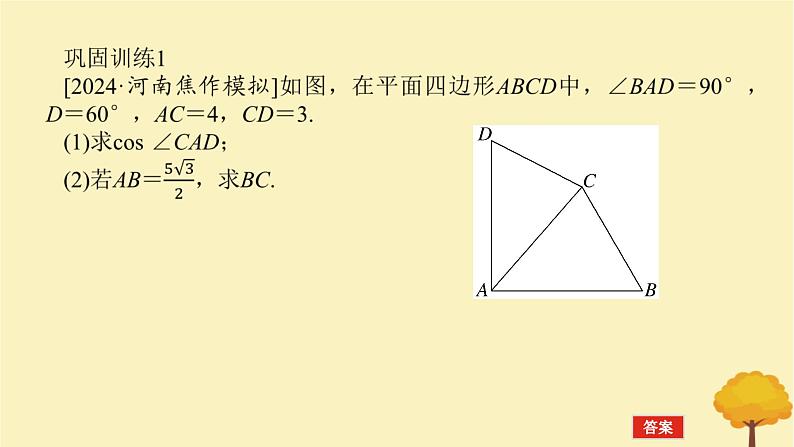
2025版高考数学全程一轮复习第四章三角函数与解三角形高考大题研究课四正弦定理余弦定理的综合应用课件
展开
这是一份2025版高考数学全程一轮复习第四章三角函数与解三角形高考大题研究课四正弦定理余弦定理的综合应用课件，共22页。
通过对任意三角形边长和角度关系的探索，会用正弦定理、余弦定理解决三角形中的综合问题，提高学生分析问题、解决问题的能力．
题后师说平面几何中解三角形问题的求解策略
题型二 三角形的中线与角平分线问题例 2 [2024·河北唐山模拟]在△ABC中，AB＝3，AC＝2，D为BC边上一点，且AD平分∠BAC.(1)若BC＝3，求CD与AD；(2)若∠ADC＝60°，设∠BAD＝θ，求tan θ.
题后师说三角形中的中线、角平分线问题的处理策略
巩固训练2[2021·新高考Ⅰ卷]记△ABC的内角A，B，C的对边分别为a，b，c.已知b2＝ac，点D在边AC上，BD sin ∠ABC＝a sin C.(1)证明：BD＝b；(2)若AD＝2DC，求cs ∠ABC.
题后师说解三角形中的最值或范围问题的2种常用方法
相关课件
2025版高考数学全程一轮复习第四章三角函数与解三角形第七节正弦定理余弦定理课件：
这是一份2025版高考数学全程一轮复习第四章三角函数与解三角形第七节正弦定理余弦定理课件，共43页。PPT课件主要包含了课前自主预习案，课堂互动探究案，RsinB，RsinC，答案C，答案D，答案B，答案A等内容，欢迎下载使用。
2024版新教材高考数学全程一轮总复习高考大题研究课四利用正弦余弦定理解三角形课件：
这是一份2024版新教材高考数学全程一轮总复习高考大题研究课四利用正弦余弦定理解三角形课件，共33页。
2024版新教材高考数学全程一轮总复习第四章三角函数与解三角形第七节正弦定理余弦定理课件：
这是一份2024版新教材高考数学全程一轮总复习第四章三角函数与解三角形第七节正弦定理余弦定理课件，共37页。PPT课件主要包含了必备知识·夯实双基，关键能力·题型突破，RsinB，RsinC，答案C，答案D，答案A，答案B，等腰或直角三角形等内容，欢迎下载使用。
