2025版高考数学全程一轮复习第一章集合与常用逻辑用语不等式第二节常用逻辑用语课件

这是一份2025版高考数学全程一轮复习第一章集合与常用逻辑用语不等式第二节常用逻辑用语课件，共39页。PPT课件主要包含了课前自主预习案，课堂互动探究案，充分不必要，必要不充分，既不充分也不必要，全称量词，存在量词，∀x∈Mpx，∀x∈M¬px，答案B等内容，欢迎下载使用。

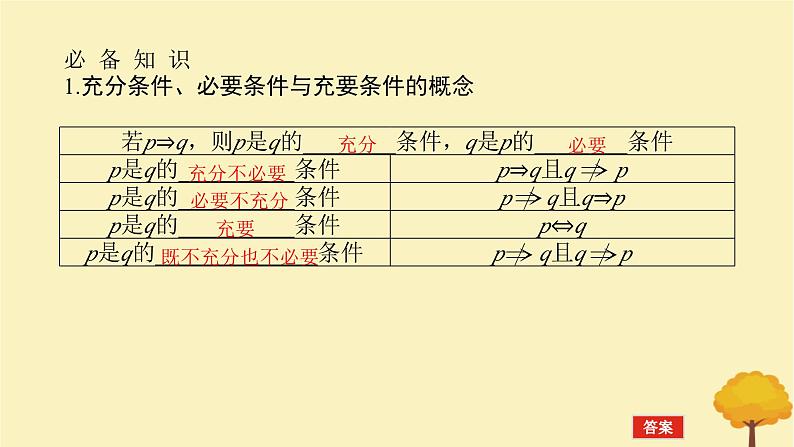
必 备 知 识1.充分条件、必要条件与充要条件的概念
2.全称量词与存在量词(1)短语“所有的”“任意一个”在逻辑中通常叫作________，用符号“______”表示．(2)短语“存在一个”“至少有一个”在逻辑中通常叫作________，用符号“______”表示．
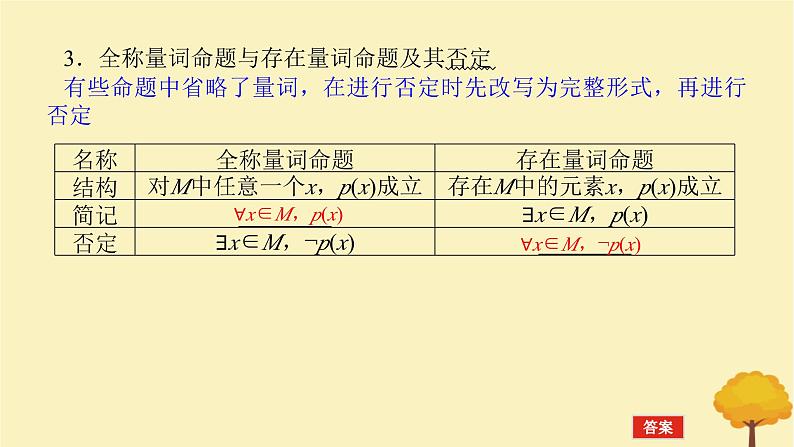
3．全称量词命题与存在量词命题及其否定 有些命题中省略了量词，在进行否定时先改写为完整形式，再进行否定
【常用结论】1．充分、必要条件与对应集合之间的关系设A＝{x|p(x)}，B＝{x|q(x)}．(1)若p是q的充分条件，则A⊆B；(2)若p是q的充分不必要条件，则A B；(3)若p是q的必要不充分条件，则B A；(4)若p是q的充要条件，则A＝B.2．含有一个量词命题的否定规律是“改变量词，否定结论”．3．命题p与p的否定的真假性相反．
夯 实 基 础1．思考辨析(正确的打“√”，错误的打“×”)(1)“长方形的对角线相等”是存在量词命题．(　　)(2)命题“对顶角相等”的否定是“对顶角不相等”．(　　)(3)当q是p的必要条件时，p是q的充分条件．(　　)(4)“若p不成立，则q不成立”等价于“若q成立，则p成立”．(　　)
2．(教材改编)“(x－1)(x＋2)＝0”是“x＝1”的(　　)A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件
解析：若x＝1，则(x－1)(x＋2)＝0显然成立，但反之不成立，即若(x－1)(x＋2)＝0，则x的值也可能为－2.故选B.
3．(教材改编)(多选)下列命题为真命题的是(　　)A．任意实数的平方大于或等于0B．对任意实数a，二次函数y＝x2＋a的图象关于y轴对称C．存在整数x，y，使得2x＋4y＝3D．存在一个无理数，它的立方是有理数
4．(易错)下面四个条件中，使a＞b成立的充分不必要条件是(　　)A．a>b＋1　 B．a>b－1C．a2>b2 D．a3>b3
解析：选项A中，a>b＋1>b，所以充分性成立，但必要性不成立，所以“a＞b＋1”为“a＞b”成立的充分不必要条件．故选A.
答案：∀x<1，0≤x≤1
1.理解充分条件、必要条件、充要条件的意义．2．理解判定定理与充分条件，性质定理与必要条件，数学定义与充要条件的关系．3．理解全称量词和存在量词的意义，能正确对两种命题进行否定．
问题思考·夯实技能【问题1】　充分条件与必要条件的两个特征是什么？
提示：(1)对称性：若p是q的充分条件，则q是p的必要条件，即“p⇒q”⇔“q⇐p”．(2)传递性：若p是q的充分(必要)条件，q是r的充分(必要)条件，则p是r的充分(必要)条件，即“p⇒q且q⇒r”⇒“p⇒r”(“p⇐q且q⇐r”⇒“p⇐r”)．
【问题2】　如何判断全称量词命题与存在量词命题的真假？
提示：(1)全称量词命题的真假判断：要判断一个全称量词命题是真命题，必须对限定集合M中的每一个元素x，验证p(x)成立；但要判断一个全称量词命题是假命题，只需列举出一个x∈M，使得p(x)不成立即可．(2)存在量词命题的真假判断：要判断一个存在量词命题是真命题，只要在限定集合M中，能找到一个x，使得p(x)成立即可；否则这一命题就是假命题．
关键能力·题型剖析题型一 充分条件、必要条件的判断例 1 (1)[2023·全国甲卷] “sin2α＋sin2β＝1”是“sinα＋cs β＝0”的(　　)A．充分条件但不是必要条件B．必要条件但不是充分条件C．充要条件D．既不是充分条件也不是必要条件
(2)[2024·重庆万州模拟]下列四个条件中，是“x解析：若x2y，此时x0，此时x题后师说充分、必要条件的两种常用判断方法
(2)a<0，b<0的一个必要条件是(　　)A．a＋b<0B．ab>2C．a－b>0D．a2－b2<0
解析：因为a<0，b<0，所以a＋b<0，所以a＋b<0是a<0，b<0的一个必要条件，若a＝－1，b＝－1，不能得到ab>2，a－b>0，a2－b2<0.
题型二 充分条件、必要条件的应用例2 已知P＝{x|x2－8x－20≤0}，非空集合S＝{x|1－m≤x≤1＋m}，若x∈P是x∈S的必要条件，则m的取值范围为________．
【变式练习】　本例中，若把“x∈P是x∈S的必要条件”改为“x∈P是x∈S的充分不必要条件”，求m的取值范围．
题后师说本例涉及参数问题，直接解决较为困难，先用等价转化思想，将复杂、生疏的问题化归为简单、熟悉的问题来解决．一般地，在涉及字母参数的取值范围的充要关系问题中，常常要利用集合的包含、相等关系来考虑，这是破解此类问题的关键．
巩固训练2已知p：关于x的方程x2－2ax＋a2＋a－2＝0有实数根，q：m－1≤a≤m＋3.若p是q的必要不充分条件，求实数m的取值范围.
解析：由题意Δ＝4a2－4(a2＋a－2)＝－4a＋8≥0，解得a≤2.所以{a|m－1≤a≤m＋3}{a|a≤2}，则m＋3≤2，解得m≤－1，所以实数m的取值范围是{m|m≤－1}．
题型三 全称量词与存在量词角度一　含有量词命题的否定例 3 (1)[2024·河北石家庄模拟]已知命题p：∃x∈R，tan x<π或ex＋2≥π，则命题p的否定为(　　)A．∃x∈R，tan x≥π或ex＋2<πB．∀x∈R，tan x<π且ex＋2≥πC．∃x∈R，tan x<π且ex＋2≥πD．∀x∈R，tan x≥π且ex＋2<π
解析：根据全称量词命题与存在量词命题的关系，因为命题p：∃x∈R，tan x<π或ex＋2≥π是存在量词命题，所以命题p的否定为∀x∈R，tan x≥π且ex＋2<π.
(2)已知命题p：∀x≥0，ex≥x2＋1，则命题p的否定为(　　)A．∀x≥0，ex解析：已知命题p：∀x≥0，ex≥x2＋1，则命题p的否定为：∃x≥0，ex题后师说对一个全称量词命题或存在量词命题进行否定时，要把命题的两个地方进行改变，一是量词符号要改变，二是结论要进行否定，即“改变量词，否定结论”．
巩固训练3(1)[2024·广东深圳模拟]命题“∀a∈N*，2a≥a2”的否定是(　　)A．∃a∈N*，2a≥a2B．∃a∈N*，2aa2
解析：“∀a∈N*，2a≥a2”是全称量词命题，它的否定是存在量词命题“∃a∈N*，2a题后师说与全称量词命题或存在量词命题真假有关的参数取值范围问题的本质是恒成立问题或有解问题．解决此类问题时，一般先利用等价转化思想将条件合理转化，得到关于参数的方程或不等式(组)，再通过解方程或不等式(组)求出参数的值或取值范围．
巩固训练4[2024·山东济南历城二中模拟]已知命题“p：∃x∈R，ax2－ax≥1”，若¬p是真命题，则实数a的取值范围是________．
随堂检测1.[2024·海南海口模拟]命题“∃x∈(－1，3)，x2－1≤2x”的否定是(　　)A．∀x∈(－1，3)，x2－1≤2xB．∃x∈(－1，3)，x2－1>2xC．∀x∈(－1，3)，x2－1>2xD．∃x∉(－1，3)，x2－1>2x
解析：∵命题“∃x∈(－1，3)，x2－1≤2x”是存在量词命题，∴它的否定是“∀x∈(－1，3)，x2－1>2x”．
2．[2024·河北石家庄模拟]“a＋1>b－2”是“a>b”的(　　)A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件
3．[2024·安徽芜湖模拟]“lg a>lg b”是“a2>b2”的(　　)A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件
解析：lg a>lg b⇔a>b>0⇒a2>b2，由a2>b2⇔|a|>|b|，不能得到a>b>0，也得不到lg a>lg b，所以lg a>lg b是a2>b2的充分不必要条件．