




2024年山东省东营市中考数学试题 (原卷版+解析版)
展开数学试题
(总分120分 考试时间120分钟)
注意事项:
1.本试题分第Ⅰ卷和第Ⅱ卷两部分,第Ⅰ卷为选择题,30分;第Ⅱ卷为非选择题,90分;本试题共6页.
2.数学答题卡共8页.答题前,考生务必将自己的姓名、准考证号、座号等填写在试题和答题卡上,考试结束,试题和答题卡一并收回.
3.第Ⅰ卷每题选出答案后,都必须用2B铅笔把答题卡上对应题目的答案标号【ABCD】涂黑.如需改动,先用橡皮擦干净,再改涂其它答案.第Ⅱ卷按要求用0.5mm碳素笔答在答题卡的相应位置上.
第Ⅰ卷(选择题 共30分)
一、选择题:本大题共10小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.
1. 绝对值是( )
A. 3B. C. D.
2. 下列计算正确的是( )
A. B.
C D.
3. 已知,直线,把一块含有角的直角三角板如图放置,,三角板的斜边所在直线交于点,则( )
A. B. C. D.
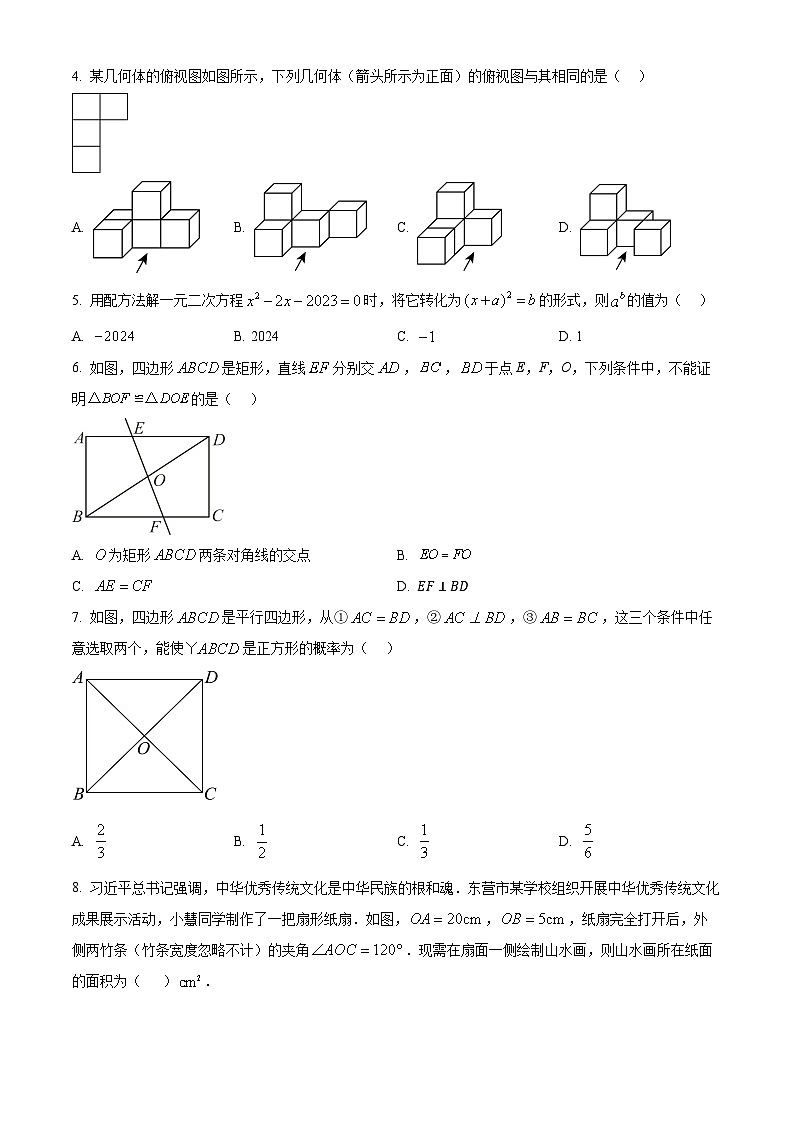
4. 某几何体的俯视图如图所示,下列几何体(箭头所示为正面)的俯视图与其相同的是( )
A. B. C. D.
5. 用配方法解一元二次方程时,将它转化为的形式,则的值为( )
A. B. 2024C. D. 1
6. 如图,四边形是矩形,直线分别交,,于点E,F,O,下列条件中,不能证明的是( )
A. 为矩形两条对角线的交点B.
C. D. EF⊥BD
7. 如图,四边形是平行四边形,从①,②,③,这三个条件中任意选取两个,能使是正方形的概率为( )
A. B. C. D.
8. 习近平总书记强调,中华优秀传统文化是中华民族的根和魂.东营市某学校组织开展中华优秀传统文化成果展示活动,小慧同学制作了一把扇形纸扇.如图,,,纸扇完全打开后,外侧两竹条(竹条宽度忽略不计)的夹角.现需在扇面一侧绘制山水画,则山水画所在纸面的面积为( ).
A. B. C. D.
9. 已知抛物线的图像如图所示,则下列结论正确的是( )
A. B.
C. D. (为任意实数)
10. 如图,在正方形中,与交于点O,H为延长线上的一点,且,连接,分别交,BC于点E,F,连接,则下列结论:①;②;③平分;④.
其中正确结论的个数是( )
A. 1个B. 2个C. 3个D. 4个
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共8小题,其中11-14题每小题3分,15-18题每小题4分,共28分.只要求填写最后结果.
11. 从2024年一季度GDP增速看,东营市增速位居山东16市“第一方阵”,一季度全市生产总值达到957.2亿元,同比增长,957.2亿用科学记数法表示为_______.
12. 因式分解:2a3-8a=______.
13. 4月23日是世界读书日,东营市组织开展“书香东营,全民阅读”活动,某学校为了解学生的阅读时间,随机调查了七年级50名学生每天的平均阅读时间,统计结果如下表所示.在本次调查中,学生每天的平均阅读时间的众数是_______小时.
14. 在弹性限度内,弹簧的长度是所挂物体质量的一次函数.一根弹簧不挂物体时长12.5cm,当所挂物体的质量为2kg时,弹簧长13.5cm.当所挂物体的质量为5kg时,弹簧的长度为_______cm,
15. 如图,将沿方向平移得到,若的周长为24cm,则四边形的周长为_______.
16. 水是人类赖以生存的宝贵资源,为节约用水,创建文明城市,某市经论证从今年1月1日起调整居民用水价格,每立方米水费上涨原价的.小丽家去年5月份的水费是28元,而今年5月份的水费则是元.已知小丽家今年5月份的用水量比去年5月份的用水量少.设该市去年居民用水价格为,则可列分式方程为_______.
17. 我国魏晋时期数学家刘徽在《九章算术注》中提到著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率的近似值为3.1416,如图,的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计的面积,可得的估计值为.若用圆内接正八边形近似估计的面积,可得的估计值为_________.
18. 如图,在平面直角坐标系中,已知直线的表达式为,点的坐标为,以为圆心,为半径画弧,交直线于点,过点作直线的垂线交轴于点;以为圆心,为半径画弧,交直线于点,过点作直线的垂线交轴于点;以为圆心,为半径画弧,交直线于点,过点作直线的垂线交轴于点;……按照这样的规律进行下去,点的横坐标是_______.
三、解答题:本大题共7小题,共62分.解答要写出必要的文字说明、证明过程或演算步骤.
19. (1)计算:;
(2)计算:.
20. 为贯彻教育部《大中小学劳动教育指导纲要(试行)》文件精神,东营市某学校举办“我参与,我劳动,我快乐,我光荣”活动.为了解学生周末在家劳动情况,学校随机调查了八年级部分学生在家劳动时间(单位:小时),并进行整理和分析(劳动时间分成五档:A档:;B档:;C档:;D档:;E档:).调查的八年级男生、女生劳动时间的不完整统计图如下:
根据以上信息,回答下列问题:
(1)本次调查中,共调查了_______名学生,补全条形统计图;
(2)调查的男生劳动时间在C档的数据是:2,2.2,2.4,2.5,2.7,2.8,2.9.则调查的全部男生劳动时间的中位数为_______小时.
(3)学校为了提高学生的劳动意识,现从E档中选两名学生作劳动经验交流,请用列表法或画树状图的方法求所选两名学生恰好都是女生的概率.
21. 如图,内接于,是的直径,点在上,点是的中点,,垂足为点D,的延长线交的延长线于点F.
(1)求证:是的切线;
(2)若,,求线段的长.
22. 如图,一次函数()的图象与反比例函数()的图象交于点,,且一次函数与轴,轴分别交于点C,D.
(1)求反比例函数和一次函数表达式;
(2)根据图象直接写出不等式的解集;
(3)在第三象限的反比例函数图象上有一点P,使得,求点的坐标.
23. 随着新能源汽车发展,东营市某公交公司计划用新能源公交车淘汰“冒黑烟”较严重的燃油公交车.新能源公交车有型和型两种车型,若购买型公交车辆,型公交车辆,共需万元;若购买型公交车辆,型公交车辆,共需万元.
(1)求购买型和型新能源公交车每辆各需多少万元?
(2)经调研,某条线路上的型和型新能源公交车每辆年均载客量分别为万人次和万人次.公司准备购买10辆型、型两种新能源公交车,总费用不超过万元.为保障该线路的年均载客总量最大,请设计购买方案,并求出年均载客总量的最大值.
24. 在中,,,.
(1)问题发现
如图1,将绕点按逆时针方向旋转得到,连接,,线段与的数量关系是______,与的位置关系是______;
(2)类比探究
将绕点按逆时针方向旋转任意角度得到,连接,,线段与数量关系、位置关系与(1)中结论是否一致?若交于点N,请结合图2说明理由;
(3)迁移应用
如图3,将绕点旋转一定角度得到,当点落到边上时,连接,求线段的长.
25. 如图,在平面直角坐标系中,已知抛物线与轴交于,两点,与轴交于点,点是抛物线上的一个动点.
(1)求抛物线的表达式;
(2)当点在直线下方的抛物线上时,过点作轴的平行线交于点,设点的横坐标为t,的长为,请写出关于的函数表达式,并写出自变量的取值范围;
(3)连接,交于点,求的最大值.时间(小时)
0.5
1
1.5
2
2.5
人数(人)
10
18
12
6
4
2024年山东省东营市垦利区中考二模数学试题(原卷版+解析版): 这是一份2024年山东省东营市垦利区中考二模数学试题(原卷版+解析版),文件包含2024年山东省东营市垦利区中考二模数学试题原卷版docx、2024年山东省东营市垦利区中考二模数学试题解析版docx等2份试卷配套教学资源,其中试卷共36页, 欢迎下载使用。
2024年山东省东营市广饶县中考一模数学试题(原卷版+解析版): 这是一份2024年山东省东营市广饶县中考一模数学试题(原卷版+解析版),文件包含2024年山东省东营市广饶县中考一模数学试题原卷版docx、2024年山东省东营市广饶县中考一模数学试题解析版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。
2024年山东省东营市垦利县中考一模数学试题(原卷版+解析版): 这是一份2024年山东省东营市垦利县中考一模数学试题(原卷版+解析版),文件包含2024年山东省东营市垦利县中考一模数学试题原卷版docx、2024年山东省东营市垦利县中考一模数学试题解析版docx等2份试卷配套教学资源,其中试卷共34页, 欢迎下载使用。












