新高中数学压轴题二轮专题专题10利用微分中值法证明不等式试题含解析答案

这是一份新高中数学压轴题二轮专题专题10利用微分中值法证明不等式试题含解析答案，共46页。试卷主要包含了解答题等内容，欢迎下载使用。

一、解答题
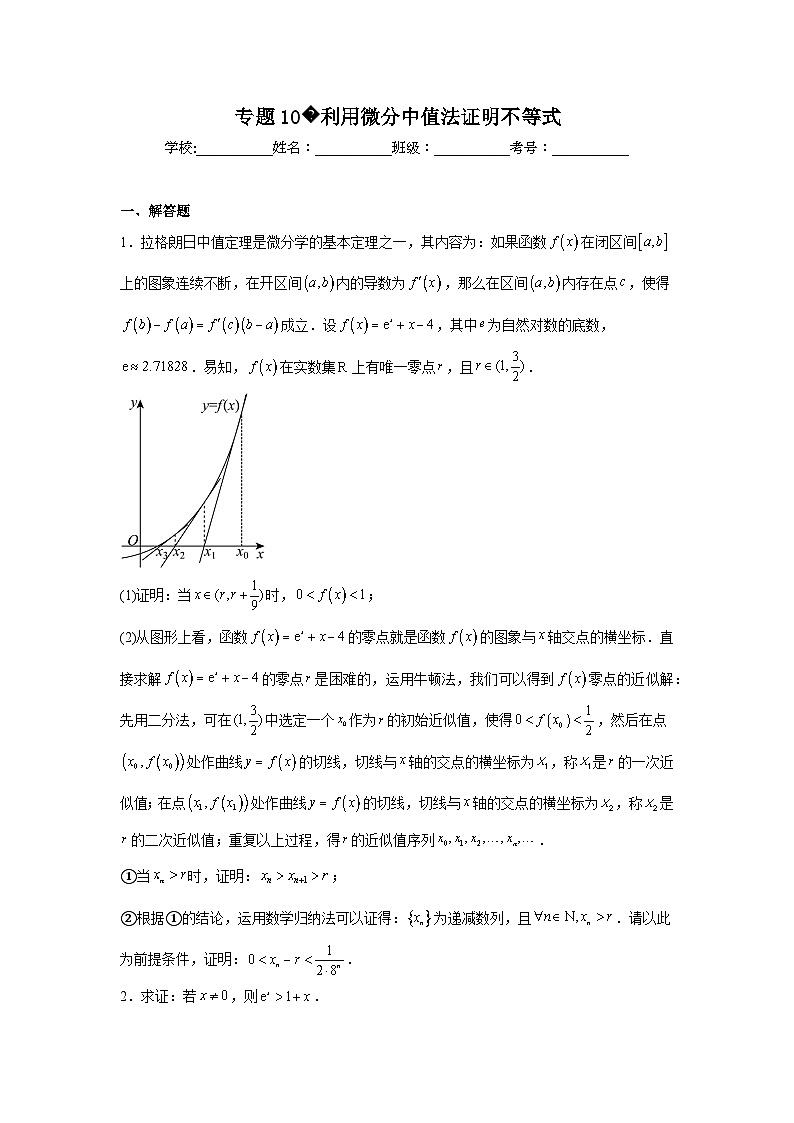
1．拉格朗日中值定理是微分学的基本定理之一，其内容为：如果函数在闭区间上的图象连续不断，在开区间内的导数为，那么在区间内存在点，使得成立．设，其中为自然对数的底数，．易知，在实数集上有唯一零点，且．
(1)证明：当时，；
(2)从图形上看，函数的零点就是函数的图象与轴交点的横坐标．直接求解的零点是困难的，运用牛顿法，我们可以得到零点的近似解：先用二分法，可在中选定一个作为的初始近似值，使得，然后在点处作曲线的切线，切线与轴的交点的横坐标为，称是的一次近似值；在点处作曲线的切线，切线与轴的交点的横坐标为，称是的二次近似值；重复以上过程，得的近似值序列．
①当时，证明：；
②根据①的结论，运用数学归纳法可以证得：为递减数列，且．请以此为前提条件，证明：．
2．求证：若，则．
3．已知函数、，的图象在处的切线与轴平行．
(1)求，的关系式并求的单调减区间；
(2)证明：对任意实数，关于的方程：在,恒有实数解；
(3)结合（2）的结论，其实我们有拉格朗日中值定理：若函数是在闭区间,上连续不断的函数，且在区间内导数都存在，则在内至少存在一点，使得．如我们所学过的指、对数函数，正、余弦函数等都符合拉格朗日中值定理条件．试用拉格朗日中值定理证明：
当时，（可不用证明函数的连续性和可导性）．
4．求证：当时，.
5．设函数，若对所有的都有成立，求证．
6．设函数．
(1)求的单调区间．
(2)求证：若对任意，都有，则．
7．变分法是研究变元函数达到极值的必要条件和充要条件，欧拉、拉格朗日等数学家为其奠定了理论基础，其中“平缓函数”是变分法中的一个重要概念．设是定义域为的函数，如果对任意的均成立，则称是“平缓函数”．
(1)若．试判断和是否为“平缓函数”?并说明理由；（参考公式：①时，恒成立；②．）
(2)若函数是周期为2的“平缓函数”，证明：对定义域内任意的，均有；
(3)设为定义在上的函数，且存在正常数，使得函数为“平缓函数”．现定义数列满足：，试证明：对任意的正整数．
（参考公式：且时，．）
8．设，证明： ．
9．已知函数，为的导函数．当时，求证：对任意的、，且，有．
10．已知函数．
（1）已知函数在点处与x轴相切，求实数m的值；
（2）求函数的单调区间；
（3）在（1）的结论下，对于任意的，证明：．
11．已知函数.
（1）求函数的最大值；
（2）设,证明.
12．已知函数．
（1）若曲线在点处的切线与直线垂直，求的值；
（2）若在区间单调递增，求的取值范围；
（3）若，证明：对任意，，，都有成立．
13．已知函数
（1）求函数的单调区间；
（2）若，对恒成立，求实数的取值范围；
（3）当时，设.若正实数，满足，，，证明：.
14．设函数，其中.
(1)若是函数的极值点，求a的值；
(2)当时，求函数的单调区间；
(3)当时，设函数，证明：.
15．已知函数，，，，求证：．
16．已知函数
（Ⅰ）讨论函数的单调性；
（Ⅱ）证明：若，则对任意，，有．
17．设是定义在上且满足下列条件的函数构成的集合：
①方程有实数解；
②函数的导数满足．
（1）试判断函数是否集合的元素，并说明理由；
（2）若集合中的元素具有下面的性质：对于任意的区间，都存在，使得等式成立，证明：方程有唯一实数解．
（3）设是方程的实数解，求证：对于函数任意的，当，时，有．
18．已知函数.
（Ⅰ）若时，，求的最小值；
（Ⅱ）设数列的通项，证明：.
19．已知函数
（1）若，求函数的单调区间；
（2）设，若对任意，恒有，求a的取值范围.
20．已知，为的导函数.
(1)若对任意都有，求的取值范围；
(2)若，证明：对任意常数，存在唯一的，使得成立.
21．已知函数．
(1)当时，求的最小值；
(2)在区间内任取两个实数p，q（pq），若不等式>1恒成立，求证：．
22．罗尔定理是高等代数中微积分的三大定理之一，它与导数和函数的零点有关，是由法国数学家米歇尔罗尔于1691年提出的．它的表达如下：如果函数满足在闭区间连续，在开区间内可导，且，那么在区间内至少存在一点，使得．
(1)运用罗尔定理证明：若函数在区间连续，在区间上可导，则存在，使得．
(2)已知函数，若对于区间内任意两个不相等的实数，都有成立，求实数的取值范围．
23．已知函数.
（1）求的单调区间；
（2）若在上恒成立，求实数的取值集合；
（3）当时，对任意的，求证：.
24．已知，函数有两个零点，记为，．
(1)证明：．
(2)对于，若存在，使得，求证：．
25．拉格朗日中值定理是微积分学的基本定理之一，它与导数和函数的零点有关，其表达如下：若函数在区间连续，在区间上可导，则存在，使得，我们将称为函数在上的“中值点”．已知函数，，．
(1)求在上的中值点的个数；
(2)若对于区间内任意两个不相等的实数，，都有成立，求实数t的取值范围．
(3)当且时，证明：．
26．已知曲线在点处的切线与曲线的另外一个交点为为线段的中点，为坐标原点．
(1)求的极小值并讨论的奇偶性．
(2)直线的斜率记为，若，，求证：．
27．设函数．
(1)讨论的单调性；
(2)若恒成立，求证：．
28．已知函数.
(1)讨论函数的单调性；
(2)设，如果对任意，，求证：.
29．已知函数．
(1)当时，求曲线在处的切线方程；
(2)若当时，，求证：．
30．设在可导，且，又对于内所有的点有证明方程在内有唯一的实根．
31．已知函数.
（1）讨论函数的单调性；
（2）若在上恒成立，求实数的取值范围；
（3）在（2）的条件下（提示：可以用第（2）问的结论），对任意的，证明：.
32．罗尔中值定理是微分学中一条重要的定理，是三大微分中值定理之一，其他两个分别为：拉格朗日中值定理、柯西中值定理．罗尔定理描述如下：如果 上的函数满足以下条件：①在闭区间上连续，②在开区间内可导，③，则至少存在一个，使得．据此，解决以下问题：
(1)证明方程在内至少有一个实根，其中；
(2)已知函数在区间内有零点，求的取值范围．
33．已知为实数，函数．
(1)当时，求在处的切线方程；
(2)定义：若函数的图象上存在两点，设线段的中点为，若在点处的切线与直线平行或重合，则函数是“中值平衡函数”，切线叫做函数的“中值平衡切线”．试判断函数是否是“中值平衡函数”？若是，判断函数的“中值平衡切线”的条数；若不是，说明理由；
(3)设，若存在，使得成立，求实数的取值范围．
参考答案：
1．(1)证明见解析；
(2)①证明见解析；②证明见解析.
【分析】（1）因为在R上单调递增，所以任意，有，另一方面，注意到，即，根据拉格明日中值定理，即可证明结论.
（2）①利用导数的几何意义进行证明即可；②根据①，及前面的结论，，，构造函数求导数，结合拉格朗日中值定理证明结论.
【详解】（1）由在R上单调递增，得任意，有，
又由，得，根据拉格明日中值定理，
存在，，
因为，所以，，
所以
（2）①先证，
在处，曲线的切线方程为，
令，得，即，
由于，在R上单调递增，则，
而，则有，所以，即；
再证：，
由于在R上单调递增，只需证，
曲线的切线方程为，即，
根据的定义，，
令，，
，，
于是在上单调递减，而，
因此，又，即，所以，
综上.
②由在R上单调递增，，得，
则，由①，及前面的结论，，，
令，则，记，则当时，
，
根据拉格朗日中值定理，
，，，
即，于是，累乘得，所以
【点睛】结论点睛：函数y=f(x)是区间D上的可导函数，则曲线y=f(x)在点处的切线方程为：.
2．证明见解析
【分析】构造函数，借助导数得其单调性后即可得证.
【详解】令，则，
当时，，当时，，
故在上单调递减，在上单调递增，
故，
故当时，.
3．(1)，减区间见解析
(2)证明见解析
(3)证明见解析
【分析】（1）由得，则，结合即可求解；
（2）将原方程转化为，得，结合零点的存在性定理即可证明；
（3）令，由拉格朗日中值定理可知存在使，结合列不等式，即可证明.
【详解】（1）因为，
由已知有，所以即，
即，由知．
当时，由得，则的减区间为，
当时，由得或，的减区间为和，
综上所述：当时，的减区间为；
当时，的减区间为和；
（2），
可化为，
令，
则，，
即，
又，所以，，即，
由零点的存在性定理知方程在区间,内必有解，
即关于的方程在,恒有实数解
（3）令，，
则符合拉格朗日中值定理的条件，即存在，
使，
因为，由，可知，
即，
.
【点睛】关键点点睛：第（2）问证明方程有解问题，时常根据已知的方程构造新函数，利用函数的零点存在性定理研究新函数的性质，进而达到解题的目的.
4．证明见解析
【分析】证法一：令，，利用拉格朗日中值定理证得，再令，即可证得结果.
证法二：令，利用拉格朗日中值定理证得，又，同时乘以，即可证得结果.
【详解】证法一：设，，则符合拉格朗日中值定理的条件，
即存在，使，
因为，由，，
可知，，
即，
可得，即有，
令，可得，即有．
证法二：原不等式可等价变形为，
令，显然它在上满足拉格朗日中值定理使用条件，
故存在，使得，
又，所以，
又因为，所以，
因此当时，，
由于，故．
【点睛】关键点点睛：本题利用拉格朗日中值定理解题，能够充分简化解题过程，关键在于函数的构造，以不等式中间的式子为基准，找到这种形式，再根据不等式的性质，去凑出所要证明的不等式.
5．证明见解析
【分析】构造函数，利用导数判断单调性并求出最值可得证.
【详解】令，则，
令，解得．
若，则对所有的，都有，∴在上单调递增，
因此，即当时，对所有的都有成立．
若，则当时，，∴在上单调递减，
因此，即当时，不一定成立．
综上，a的取值范围是，即．
6．(1)单调递增区间为，单调递减区间为
(2)证明见解析
【分析】（1）求导，判断导数正负得到单调区间；
（2）当时，a取任意值；当时，转化为，即．令，则在上至少存在一点，使，令，利用导数求出的最大值得证.
【详解】（1），令，得，或．
所以当时，；
当时，．
所以的单调递增区间为，
单调递减区间为．
（2）①当时，恒成立，此时a取任意值．
②当时，转化为，则．
令，则在上至少存在一点，使．
所以．
设，则，．
令．
令，则，所以．
易知当时，，所以．
综合①②可知，．
7．(1)函数是“平缓函数”； 是上的“平缓函数”，理由见解析；
(2)证明见解析
(3)证明见解析.
【分析】（1）利用 “平缓函数”的顶用判断可得答案；
（2）设，且，分和，借助“平缓函数”的定义证明即可；
（3）由为上的“平缓函数”，且得，则对任意的，利用证明可得.
【详解】（1）对于函数，
由对任意的，且，
则，即，
，
因此函数是“平缓函数”；
对于函数，由对任意的，且，
，
可知函数是上的“平缓函数”
（2）由周期性可得，由于函数是周期函数，
故不妨设，且，
当时，由为上的“平缓函数”得；
当时，不妨设，此时由为上的“平缓函数”得
．
故对定义域内任意的，且均有．
（3）由为上的“平缓函数”，且得，则对任意的，
，
因此
，得证．
【点睛】思路点睛：本题主要是根据 “平缓函数”的定义和性质进行判断.
8．证明见解析
【分析】构造函数，借助拉格朗日中值定理，即可得证.
【详解】证明：
设，，显然在满足拉格朗日中值定理的条件，
则，使得，
而，所以．
由知在上单调递增，
从而有
即有.
9．证明见解析
【分析】令，作差可得出，利用导数证明出，然后利用导数证明出，即可证得结论成立.
【详解】证明：由，得．
对任意的、，且，令，
则
． ①
令，当时，，
由此可得在单调递增，所以当时，，即．
因为，，，
所以． ②
令，其中，
则，
所以，函数在上单调递增，可知，当时，，
即，故． ③
由①②③可得．
所以，当时，对任意的、，且，有．
【点睛】方法点睛：利用导数证明不等式问题，方法如下：
（1）直接构造函数法：证明不等式（或）转化为证明（或），进而构造辅助函数；
（2）适当放缩构造法：一是根据已知条件适当放缩；二是利用常见放缩结论；
（3）构造“形似”函数，稍作变形再构造，对原不等式同解变形，根据相似结构构造辅助函数.
10．（1）；（2）在递增，在上递减；（3）证明见解析.
【分析】（1）函数在点处与x轴相切，可得，从而可求出实数m的值；
（2）分和两种情况由导数的正负可求出函数的单调区间，
（3）由（1）知，得，所以对于任意的，可化为，令，则，再结合（2）可得结论
【详解】解：由得
（1）依题意得，即
（2）当时，，知函数在递增；
当时，，由得，由得即函数在递增，在上递减．
（3）由（1）知，得，
对于任意的，可化为
其中
，其中，
令，则问题转化为，即
由（2）知，函数在递减，且，于是上式成立
故对于任意的成立．
11．（1）0；(2)详见解析.
【分析】（1）先求出函数的定义域，然后对函数进行求导运算，令导函数等于0求出x的值，再判断函数的单调性，进而可求出最大值．（2）先将代入函数得到的表达式后进行整理，根据（1）可得到，将放缩变形为代入即可得到左边不等式成立，再用根据的单调性进行放缩．然后整理即可证明不等式右边成立．
【详解】(1）由已知可得x>-1, -1，令0得x=0.
当-10时，1即函数的图象在区间上的任意两点连线的斜率大于1，
即在内恒成立，
等价于当时，恒成立，
设，，则，
若，则，
当时，，在递减，
当时，，在递增，
∵，，
∴
又，
，
故，实数a的取值范围是．
22．(1)证明见解析
(2)
【分析】（1）根据给定条件，构造函数，利用导数结合罗尔定理推导即得．
（2）求出函数的导数，利用（1）的结论建立恒成立的不等式，再利用导数求出函数的值域即得．
【详解】（1）令，则，
令函数，则，
显然在上连续，且在上可导，由罗尔定理，存在，使得，
即，∴．
（2）依题意，，
不妨令，则恒成立，
由（1）得，于是，即，
因此，令，
求导得，函数在上单调递增，则，
而函数在上单调递增，其值域为，则，
∴实数的取值范围是．
【点睛】思路点睛：涉及函数新定义问题，理解新定义，找出数量关系，联想与题意有关的数学知识和方法，构造函数，转化、抽象为相应的函数问题作答．
23．（1）当时减区间为，当时递增区间为，递减区间为；（2）；（3）证明见解析.
【分析】（1）讨论、两种情况，先求出，令得减区间，令的增区间；
（2）当时在上不可能恒成立，当时，利用单调性求出为，可证明；
（3）转化，利用只需证明.
【详解】（1），
当时，，减区间为；
当时，由得，由得，
∴递增区间为，递减区间为.
（2）由（1）知，当时，在上为递减，而，
∴在上不可能恒成立；
当时，在上递增，在上递减，
，令，
依题意有，而，且，
∴在上递减，在上递增，∴，故.
（3）由（2）知：时，恒成立，所以有.
则，
又由知在上恒成立，
∴.
综上所述：对任意的，有.
【方法点睛】本题主要考查利用导数研究函数的单调性、不等式恒成立及不等式的证明，属于难题.不等式证明问题是近年高考命题的热点，命题主要是和导数、绝对值不等式及柯西不等式相结合，导数部分一旦出该类型题往往难度较大，要准确解答首先观察不等式特点，结合已解答的问题把要证的不等式变形，并运用已证结论先行放缩，然后再化简或者进一步利用导数证明.
24．(1)证明见解析
(2)证明见解析
【分析】（1）函数有两个零点，则方程有两个根，，利用导数求函数单调区间，得到零点的范围，再结合单调性证明不等式；
（2）由已知得，， ，设，通过构造函数，利用导数研究单调性，证明，再由在上是增函数，得证．
【详解】（1）证明：∵函数有两个零点，∴方程有两个根．
令，则，
时，；时，，
∴在上单调递增，在上单调递减，
因此在处取得最大值，
∴，即有，且有．
又，，结合函数的单调性可得，，
∴．
（2）证明：由，
得．
而由得，
∴．
设，则．
令，则，
∴在上是增函数，因此，故．
又，，即，∴，
从而，即．
又∵在上是增函数，∴，即．
25．(1)在上的中值点有且只有1个
(2)
(3)证明见解析
【分析】（1）求导函数，结合中值定理求解，于是可得，设，求导确定其单调性，判断函数的零点，从而得在上的中值点的个数；
（2）不妨设，则，将不等式转化为，从而可得函数与在上的单调性，转而可得恒成立，求导确定最值即可得实数t的取值范围；
（3）由拉格朗日中值定理值可得在或上总存在，使得，从而有，根据（2）中结论，即可证得答案.
【详解】（1），，
因为，，
所以，即，
令，则，
则在上，，单调递减；在上，，单调递增，
因为，
所以在上存在唯一一零点，在上无零点；
即在上存在唯一解，所以在上的中值点有且只有1个；
（2）不妨设，则，故有，
即，即，
因为上式对任意的都成立，
所以函数和在上均单调递增，
等价于，，
又函数中，，
当时，，则单调递减，
当时，，则单调递增.
所以，从而.
又函数，则，则在上单调递增，
所以，从而.
综上所述，实数的取值范围是.
（3）证明：，
由拉格朗日中值定理值，在或上总存在，
使得，即，
由（2）知，所以，
所以.
26．(1)，答案见解析
(2)证明见解析
【分析】（1）由导函数的正负可知函数在上单调递增，在上单调递减，则极小值为，然后根据奇偶性的定义，讨论参数即可判断函数的奇偶性；
（2）由导函数求出在点点处的斜率，并根据点斜式写出切线方程，联立曲线方程可求得B点坐标，再根据中点坐标公式求出P点坐标，并求得直线OP的斜率，将，，转化为恒成立问题，设，求出其最小值，可得实数的取值范围．
【详解】（1）已知，，
则，
当时，，
当或时，，
在上单调递增，在上单调递减，
则当时，取得极小值，
当时，，显然，
且，为奇函数；
当时，，
∴为非奇非偶函数．
综上所述，的极小值为；当时，为奇函数，
当时，为非奇非偶函数．
（2）由（1）知，∴曲线在点处的切线方程为：
，
其与原曲线方程联立化简得：，
从而，
由于P为线段的中点，∴，
则直线OP的斜率，
由于，，即当时，恒有，
令，则，
易知当时，，
当时，，
即在上单调递减，在上单调递增，
∴当时，，
∴，
从而实数的取值范围为．
【点睛】关键点点睛：最后一问关键点在于将原问题转化为转化为恒成立，从而可构造相应函数，借助导数解决问题.
27．(1)答案见解析
(2)证明见解析
【分析】（1）求出导数后，分及讨论即可得；
（2）结合（1）中所得单调性，可得，此时可得函数最小值，则该最小值需大于等于零恒成立，构造相应函数，求出导数。结合函数单调性与最值即可得解.
【详解】（1）的定义域为，，
若，则，在上单调递增．
若，则当时，，单调递减；
当时，，单调递增；
（2）由（1）知，若，则当时，，矛盾，
因此，由（1）知此时，
恒成立等价于恒成立，
设，则，
故在上单调递增，在上单调递减，
∴有．又恒成立，
则必有，根据的单调性及，知．
28．(1)答案见解析
(2)证明见解析
【分析】（1）先确定函数的定义域，然后求导，在函数定义域内求解和，即可求出单调区间；
（2）根据（1）中单调性的结论，写出的等价形式，,再转化为研究在上单调递减，最后利用分离参数法即可证明出a的范围.
【详解】（1）函数定义域为，，
①当时，，在单调递增；
②当时，，在单调递减；
③当时，由得，
所以在单调递增，在单调递减.
（2）证明：不妨设而当时，
由（1）可知在单调递减，
从而 ，等价于，.
构造函数，只需在单调递减，
即在恒成立，
分离参数法：，只需.
【点睛】方法点睛：已知函数恒成立，求参数值(取值范围)常用的方法：
（1）分离参数法：先将参数分离，转化成求函数的值域问题加以解决；
（2）数形结合法：先对解析式变形，进而构造两个函数，然后在同一平面直角坐标系中画出函数的图象，利用数形结合的方法求解.
29．(1)
(2)
【分析】（1）先求的定义域，再求，，，由直线方程的点斜式可求曲线在处的切线方程为
（2）构造新函数，对实数分类讨论，用导数法求解．
【详解】（1）的定义域为．当时，
，
曲线在处的切线方程为
故切线方程为
（2）当时，等价于
设，则，
（i）当，时，，
故在上单调递增，因此；
（ii）当时，令得
．
由和得，故当时，，在单调递减，
因此．
综上，的取值范围是
故答案为
30．证明见解析
【分析】根据函数零点存在原理，结合拉格朗日中值定理进行证明即可.
【详解】令，又∵，则
∴函数g（x）在（0，1）内至少有一个实根．
假设方程在（0，1）内有两个实根不妨设为，
则有，对函数）在上运用拉格朗日中值定理有
．因此
这和已知条件矛盾．∴方程在（0，1）内有唯一的实根．
31．（1）答案见解析；（2）；（3）证明见解析.
【分析】（1）求导，对参数进行分类讨论，即可确定其单调性；
（2）由（1）中所求函数单调性，将问题转化为求不等式的解集；再构造函数，根据其单调性，即可求得参数的范围；
（3）根据（2）中的结论，令，将目标函数进行转化，即可证明不等式.
【详解】（1）函数的定义域为，.
①当时，在上恒成立，所以在上单调递增.
②当时，令，得，
所以在上单调递增；
令，得，所以在上单调递减.
综上，当时，的的的递增区间是；
当时，的的的递增区间是，
单调递减区间是.
（2）由题意得，由（1）知，当时，不满足题意，
故，则在上单调递增，在上单调递减，
所以，故只需即可.
令，则，
所以当时，；当，，
所以在上单调递减，在上单调递增，
所以，即.
又∵，
所以，解得.
综上，m的取值范围是.
（3），
因为，所以，
由（2）得，时，（时，等号成立）
令，则，
因为，所以，即.
因为，所以，即.
【点睛】该题考查的是有关应用导数研究函数的问题，涉及的知识点有利用导数研究函数的单调性，根据恒成立求参数的取值范围，利用导数证明不等式，属于较难题目.
32．(1)证明见解析；
(2).
【分析】（1）根据导数运算构造函数，验证函数满足罗尔中值定理的条件，根据罗尔中值定理完成证明；
（2）设，且，由罗尔中值定理可得至少有两个解，利用导数分析函数的单调性，结合零点存在性定理列不等式求的取值范围．
【详解】（1）设，
则，
所以函数在上连续，在区间上可导，
又，故，
所以由罗尔中值定理可得至少存在一个，使得，
所以，
所以方程在内至少有一个实根，
（2）因为函数在区间内有零点，
不妨设其零点为，则，，
由可得，
所以函数在上连续，在上可导，
又，，
由罗尔中值定理可得至少存在一个，使得，
因为函数在上连续，在上可导，
又，，
由罗尔中值定理可得至少存在一个，使得，
所以方程在上至少有两个不等的实数根，
设，
则，
当时，，函数在上单调递增，
所以方程在上至多有一个根，矛盾，
当时，，函数在上单调递减，
所以方程在上至多有一个根，矛盾，
当时，由，可得，，
当时，，函数在上单调递减，
当时，，函数在上单调递增，
所以当时，函数取最小值，
又，
所以，
又，，
由零点存在性定理可得，，
所以，，又，
所以，
所以的取值范围．
【点睛】关键点点睛：“新定义”主要是指即时定义新概念、新公式、新定理、新法则、新运算五种，然后根据此新定义去解决问题，有时还需要用类比的方法去理解新的定义，这样有助于对新定义的透彻理解.但是，透过现象看本质，它们考查的还是基础数学知识，所以说“新题”不一定是“难题”，掌握好三基，以不变应万变才是制胜法宝.
33．(1)
(2)当时，函数是“中值平衡函数”，且函数的“中值平衡切线”有无数条；当时，不是“中值平衡函数”，理由见解析；
(3)
【分析】（1）求导，利用导数的几何意义求切线方程；
（2）先利用“中值平衡函数”的定义将其化为能否成立，再讨论与，构造函数，利用导数研究函数的单调性，进而判定函数是否是“中值平衡函数”，是否存在“中值平衡切线”；
（3）将化为，构造函数，求导，通过研究导数的符号得到函数的单调性进而求最值，得到参数的范围．
【详解】（1）函数的定义域为，，
当时，，
∴在处的切点坐标为，切线斜率为，切线方程为．
（2）若函数是“中值平衡函数”，则存在，
使得，即，
（※）
①当时，（※）对任意的都成立，
∴函数是“中值平衡函数”，且函数的“中值平衡切线”有无数条；
②当时，有，设，则方程在区间上有解，
记函数，则，∴函数在区间单调递增，
∵，∴当时，，
即方程在区间上无解，即函数不是“中值平衡函数”；
综上所述，当时，函数是“中值平衡函数”，且函数的“中值平衡切线”有无数条；当时，不是“中值平衡函数”；
（3）由，得，
记，，
∴当时，，单调递减，当时，，单调递增；
∴，
，记，
，，
，
时，，单调递减；时，，单调递增；
，，
故实数的取值范围为．