青岛版（2024）七年级上册2.1 有理数的加法与减法精品ppt课件

这是一份青岛版（2024）七年级上册2.1 有理数的加法与减法精品ppt课件，共60页。PPT课件主要包含了知识点，有理数的加法，知1－讲，知1－练，知2－讲，有理数的加法运算律，知2－练，同分母相结合，知3－讲，有理数的减法等内容，欢迎下载使用。
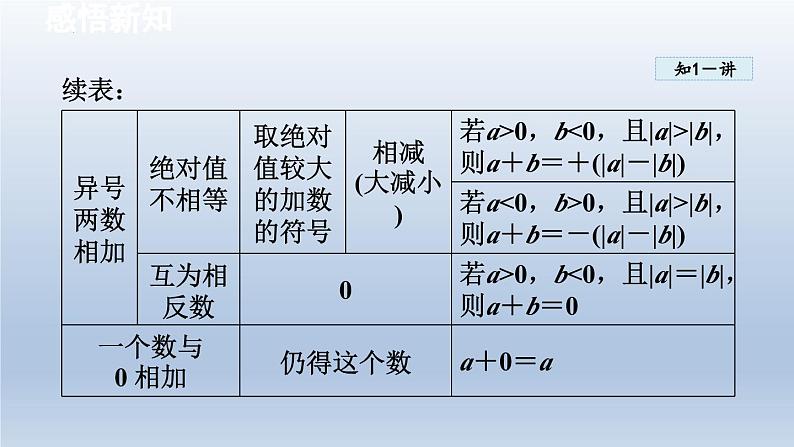
1. 有理数加法法则(1)同号两数相加，取相同的符号，并把绝对值相加.(2)绝对值不相等的异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值. 互为相反数的两个数相加得0 .(3)一个数同0 相加，仍得这个数.
2. 有理数加法运算的各种情况如下表
3. 有理数加法法则的记忆口诀同号相加一边倒；异号相加“大”减“小”，符号跟着“大”的跑；绝对值相等“零”正好；加数如果遇到零，和是自身要记牢.注：“大”或“小”是指两个加数绝对值的大小.
特别提醒若a＋b＝0，则a＝－b.若a＋b＝0，且a ≥ 0，b ≥ 0，则a＝b＝0.
特别解读1. 若两个数的和为正数，则这两个加数有三种可能：(1)两个都是正数；(2)一个是正数、一个是负数，且正数的绝对值大于负数的绝对值；(3)一个是正数、一个是0.
2. 若两个数的和为负数，则这两个加数有三种可能：(1)两个都是负数；(2)一个是正数、一个是负数，且负数的绝对值大于正数的绝对值；(3)一个是负数、一个是0.
解题秘方：先确定两个数相加的类型，然后根据法则计算.
1-1. [月考·淄博张店区]已知|a|＝3，|b|＝4， 并且a>b，那么a＋b的值为(　　)A. ＋7 B. －7C. ±1 D. －7 或－1
解：(－19)＋(－91)＝－(19＋91)＝－110.
(－2.4)＋(＋2.4)＝0.
列式计算：(1)求比－18大－30的数；(2)求绝对值大于2.6而小于5.3的所有负数之和.
解题秘方：根据题意列式计算，理解题意是解题的关键.
解：(1)(－18)＋(－30)＝－(18＋30)＝－48.(2)(－3)＋(－4)＋(－5)＝－(3 ＋4 ＋5)＝－12 .
(2)从水面开始，某潜水员先潜入水下61 m，然后又上升 30 m，这时潜水员在什么位置？
解：由题意，可将潜入水下61 m记作－61 m，上升30m记作＋30 m，则－61＋30＝－(61－30)＝－31(m)．所以这时潜水员在水下31 m处．
1. 有理数的加法运算律
2. 有理数加法运算律的运用技巧灵活运用有理数的加法运算律，能使运算过程简化，通常有以下规律：①互为相反数的两数先相加—“相反数结合法”；②符号相同的数先相加—“同号结合法”；③分母相同的数先相加—“同形结合法”；
④相加能得到整数的数先相加—“凑整法”；⑤ 带分数相加时，先拆成整数和真分数的和，再利用加法的运算律进行相加—“拆项结合法”.
特别提醒1. 有理数的加法运算律不但适用于两个数或三个数相加，而且适用于三个以上有理数相加.2. 利用有理数的加法交换律时，要适当加括号，如－6.6＋2＋(－3.4)＝2＋(－6.6)＋(－3.4).3. 根据需要灵活运用加法运算律，可以达到简化计算的 目的.
解题秘方：先找相反数，然后利用加法的交换律和结合律将相反数结合计算.
3-1.计算：(1)25.7＋(－7.3)＋(－13.7)＋7.3；(2)(－3)＋(－2)＋(－1)＋0＋1＋2；(3)143＋(－87)＋27＋(－143).
解：原式＝[25.7＋(－13.7)]＋[(－7.3)＋7.3]＝12＋0＝12.
原式＝(－3)＋[(－2)＋2]＋[(－1)＋1]＋0＝－3.
原式＝[143＋(－143)]＋[(－87)＋27]＝0＋(－60)＝－60.
计算： 43＋(－77)＋37＋(－23) .
解题秘方：先把正数、负数分别结合，再计算.
解：原式＝(43＋37)＋[(－77)＋(－23)]＝80＋(－100)＝－20.
4-1.计算：(1)18＋(－17)＋7＋(－8)；(2)23＋(－17)＋6＋(－22).
解：原式＝(18＋7)＋[(－17)＋(－8)]＝25＋(－25)＝0.
原式＝(23＋6)＋[(－17)＋(－22)]＝29＋(－39)＝－10.
解题秘方：将同分母的分数结合在一起计算.
解：原式＝[(－3.14)＋2.14]＋[4.96＋(－7.96)]＝(－1)＋(－3)＝－4.
解题秘方：从分析材料中的计算方法，先将带分数拆分为一个整数和一个真分数的和，然后重新组合分组(整数一组，分数一组)，最后分别计算求值.
公路养护小组开车沿南北公路巡视维护， 某天早晨从A地出发， 晚上到达B地， 规定向北为正方向， 当天的行驶记录如下(单位： km)：＋18，－9，＋7， －14，＋15，－6，－8 .
(1)问B地在A地的哪个方向， 距离多少千米？
解题秘方：直接把原数相加，和为正，则在A地的北边；和为负，则在A地的南边.
解：(＋18)＋(－9)＋(＋7)＋(－1 4)＋(＋15)＋(－6)＋(－8)＝[(＋18 )＋(＋7)＋(＋15 )]＋[(－9)＋(－14)＋(－6)＋(－8)]＝(＋40)＋(－37)＝ 3(km).故B地在A地的北边3 km处．
(2)若汽车每千米耗油a L ， 求该天共耗油多少升.
解题秘方：把原数的绝对值相加，再乘a.
解：(|＋18|＋|－9|＋|＋7|＋|－14|＋|＋15|＋|－6|＋|－8|) ×a＝(18＋9＋7＋14＋15＋6＋8)×a＝77a(L).故该天共耗油77a L．
8-1. 某气象员为了掌握某一周内天气的变化情况，测量了这周从星期一到星期日的最低气温. 下表是这周内的最低气温的变化情况(正数表示比前一日最低气温上升, 负数表示比前一日最低气温下降)：
试分析这周内最低气温的总体变化情况.
解：2＋(－1)＋(－2)＋4＋(－2.5)＋1＋0.5＝[2＋(－2)]＋[(－1)＋1]＋4＋[(－2.5)＋0.5]＝0＋0＋4＋(－2)＝2(℃)．所以这周内最低气温总体上升了2 ℃.
1. 有理数减法法则减去一个数，等于加上这个数的相反数.用字母表示：a－b＝ a＋(－b)，其中a，b表示任意有 理数.
特别提醒：有理数的减法是有理数的加法的逆运算，进行减法运算时，常将减法转化为加法再计算，转化过程中，应注意“两变一不变”.“两变”是指运算符号“－”号变成“＋”号，减数变成它的相反数；“一不变”是指被减数不变.
特别解读有理数的减法，需要先将减法转化为加法，再按有理数的加法法则和运算律计算.有理数的减法在转化为加法之前，被减数与减数的位置不能改变.
2. 两数相减差的符号(1)较大数－较小数＝正数，即若a>b，则a－b> 0 .(2)较小数－较大数＝负数，即若a0B. 若a>0，b0C. 若a0，则a－b