



新高考数学一轮复习讲义 第10讲 指数与指数函数(2份打包,原卷版+含解析)
展开一、知识点梳理
1.指数及指数运算
(1)根式的定义:
一般地,如果 SKIPIF 1 < 0 ,那么 SKIPIF 1 < 0 叫做 SKIPIF 1 < 0 的 SKIPIF 1 < 0 次方根,其中 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,记为 SKIPIF 1 < 0 , SKIPIF 1 < 0 称为根指数, SKIPIF 1 < 0 称为根底数.
(2)根式的性质:
当 SKIPIF 1 < 0 为奇数时,正数的 SKIPIF 1 < 0 次方根是一个正数,负数的 SKIPIF 1 < 0 次方根是一个负数.
当 SKIPIF 1 < 0 为偶数时,正数的 SKIPIF 1 < 0 次方根有两个,它们互为相反数.
(3)指数的概念:指数是幂运算 SKIPIF 1 < 0 中的一个参数, SKIPIF 1 < 0 为底数, SKIPIF 1 < 0 为指数,指数位于底数的右上角,幂运算表示指数个底数相乘.
(4)有理数指数幂的分类
①正整数指数幂 SKIPIF 1 < 0 ;②零指数幂 SKIPIF 1 < 0 ;
③负整数指数幂 SKIPIF 1 < 0 , SKIPIF 1 < 0 ;④ SKIPIF 1 < 0 的正分数指数幂等于 SKIPIF 1 < 0 , SKIPIF 1 < 0 的负分数指数幂没有意义.
(5)有理数指数幂的性质
① SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 ;② SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 ;
③ SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 ;④ SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 .
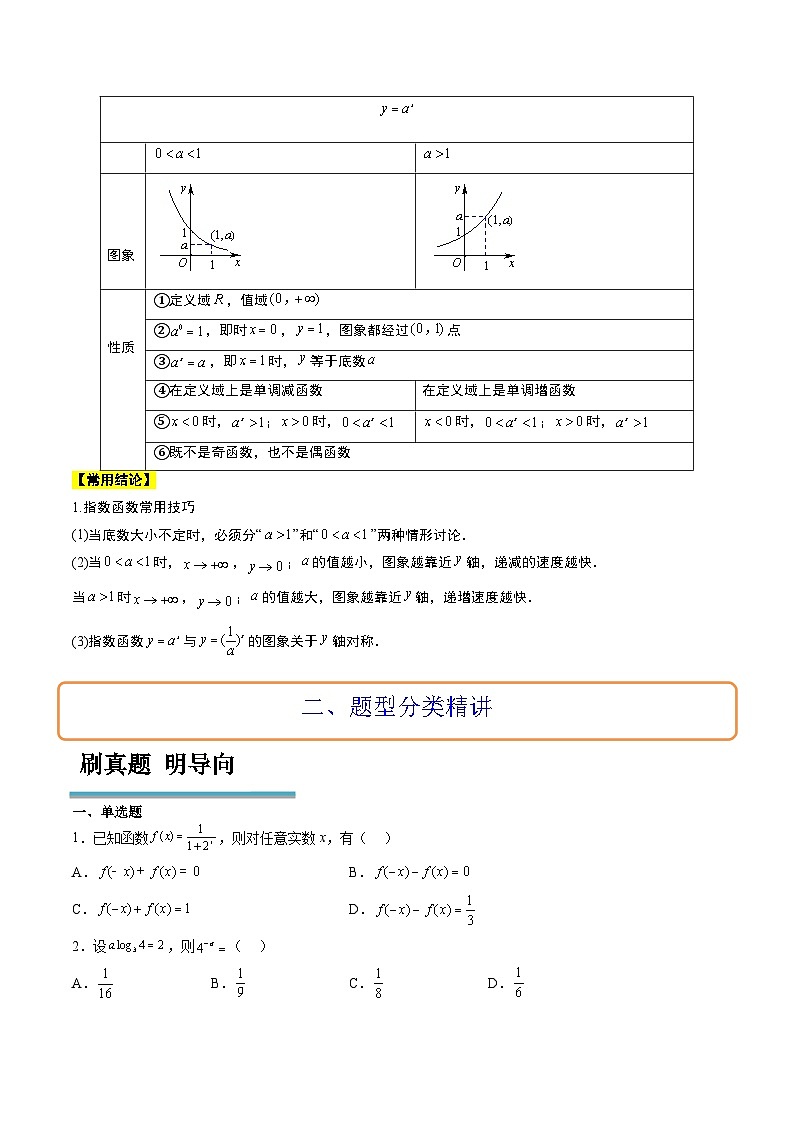
2.指数函数
【常用结论】
1.指数函数常用技巧
(1)当底数大小不定时,必须分“ SKIPIF 1 < 0 ”和“ SKIPIF 1 < 0 ”两种情形讨论.
(2)当 SKIPIF 1 < 0 时, SKIPIF 1 < 0 , SKIPIF 1 < 0 ; SKIPIF 1 < 0 的值越小,图象越靠近 SKIPIF 1 < 0 轴,递减的速度越快.
当 SKIPIF 1 < 0 时 SKIPIF 1 < 0 , SKIPIF 1 < 0 ; SKIPIF 1 < 0 的值越大,图象越靠近 SKIPIF 1 < 0 轴,递增速度越快.
(3)指数函数 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的图象关于 SKIPIF 1 < 0 轴对称.
二、题型分类精讲
刷真题 明导向
一、单选题
1.已知函数 SKIPIF 1 < 0 ,则对任意实数x,有( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0
C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
2.设 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 ( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
3.已知函数 SKIPIF 1 < 0 是偶函数,当 SKIPIF 1 < 0 时, SKIPIF 1 < 0 ,则该函数在 SKIPIF 1 < 0 上的图像大致是( )
A.B.
C.D.
4.下列函数中最小值为4的是( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0
C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
5.已知 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 ( )
A.25B.5C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
6.若 SKIPIF 1 < 0 ,则( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
7.设 SKIPIF 1 < 0 ,则( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
题型一 指数幂的化简与求值
策略方法指数幂运算的一般原则
(1)有括号的先算括号里的,无括号的先算指数运算.
(2)先乘除后加减,负指数幂化成正指数幂的倒数.
(3)底数是负数,先确定符号;底数是小数,先化成分数;底数是带分数的,先化成假分数.
(4)若是根式,应化为分数指数幂,尽可能用幂的形式表示,运用指数幂的运算性质来解答.
【典例1】计算:
(1) SKIPIF 1 < 0 ; (2)已知: SKIPIF 1 < 0 ,求 SKIPIF 1 < 0 的值.
【题型训练】
一、单选题
1. SKIPIF 1 < 0 ( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
2.下列结论中,正确的是( )
A.设 SKIPIF 1 < 0 则 SKIPIF 1 < 0 B.若 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 SKIPIF 1 < 0
C.若 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 D. SKIPIF 1 < 0
二、填空题
3.若 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 ______
4.已知 SKIPIF 1 < 0 ,化简二次根式 SKIPIF 1 < 0 的值是________
5.已知 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 =__________
6.已知 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 的值为__________.
三、解答题
7.(1)计算 SKIPIF 1 < 0 ;
(2)若 SKIPIF 1 < 0 ,求 SKIPIF 1 < 0 的值.
8.(1)计算: SKIPIF 1 < 0 ;
(2)已知 SKIPIF 1 < 0 是方程 SKIPIF 1 < 0 的两根,求 SKIPIF 1 < 0 的值.
题型二 指数函数的图像与性质
策略方法 解决指数函数有关问题,思路是从它们的图像与性质考虑,按照数形结合的思路分析,从图像与性质找到解题的突破口,但要注意底数对问题的影响.
【典例1】函数 SKIPIF 1 < 0 有两个不同的零点,则 SKIPIF 1 < 0 ( SKIPIF 1 < 0 且 SKIPIF 1 < 0 )的图象可能为( )
A. B.
C. D.
【典例2】已知函数 SKIPIF 1 < 0 的图像恒过一点P,且点P在直线 SKIPIF 1 < 0 的图像上,则 SKIPIF 1 < 0 的最小值为( )
A.4B.6C.7D.8
【典例3】比较下列几组值的大小:
(1) SKIPIF 1 < 0 和 SKIPIF 1 < 0 ; (2) SKIPIF 1 < 0 和 SKIPIF 1 < 0 ;
(3) SKIPIF 1 < 0 和 SKIPIF 1 < 0 ; (4) SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 .
【题型训练】
一、单选题
1.如图中,①②③④中不属于函数 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 中一个的是( )
A.①B.②C.③D.④
2.函数 SKIPIF 1 < 0 ( SKIPIF 1 < 0 且 SKIPIF 1 < 0 )与函数 SKIPIF 1 < 0 的图象可能是( )
A.B.
C.D.
3.函数 SKIPIF 1 < 0 (其中 SKIPIF 1 < 0 , SKIPIF 1 < 0 )的图象恒过的定点是( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
4.已知函数 SKIPIF 1 < 0 ( SKIPIF 1 < 0 且 SKIPIF 1 < 0 )的图象过定点 SKIPIF 1 < 0 ,则不等式 SKIPIF 1 < 0 的解集为( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
5.函数 SKIPIF 1 < 0 的图像恒过定点A,若点A在双曲线 SKIPIF 1 < 0 上,则m-n的最大值为( )
A.6B.-2C.1D.4
6.已知 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 ,则( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0
C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
7.设函数 SKIPIF 1 < 0 ,若 SKIPIF 1 < 0 为增函数,则实数 SKIPIF 1 < 0 的取值范围是( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0
C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
8.已知 SKIPIF 1 < 0 ,则( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0
C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
二、多选题
9.点 SKIPIF 1 < 0 在函数 SKIPIF 1 < 0 的图象上,当 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 可能等于( )
A.-1B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D.0
三、填空题
10.请写出一个同时满足下列条件①②③的函数 SKIPIF 1 < 0 ____________.
① SKIPIF 1 < 0 ;②对任意 SKIPIF 1 < 0 ,当 SKIPIF 1 < 0 时, SKIPIF 1 < 0 ;③ SKIPIF 1 < 0 .
11.已知 SKIPIF 1 < 0 为 SKIPIF 1 < 0 上的奇函数,当 SKIPIF 1 < 0 时, SKIPIF 1 < 0 ,则不等式 SKIPIF 1 < 0 的解集为___________.
12.若函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递减,则k的取值范围为____________.
四、解答题
13.已知函数 SKIPIF 1 < 0 (a为常数)和函数 SKIPIF 1 < 0 ,且 SKIPIF 1 < 0 为奇函数.
(1)求实数a的值;
(2)设不等式 SKIPIF 1 < 0 恒成立,试求实数 SKIPIF 1 < 0 的范围.
题型三 解指数方程与不等式
策略方法 指数方程或不等式的解法
(1)解指数方程或不等式的依据
①af (x)=ag(x)⇔f (x)=g(x).
②af (x)>ag(x),当a>1时,等价于f (x)>g(x);
当0<a<1时,等价于f (x)<g(x).
(2)解指数方程或不等式的方法
先利用幂的运算性质化为同底数幂,再利用函数单调性转化为一般不等式求解.
【典例1】不等式 SKIPIF 1 < 0 对于 SKIPIF 1 < 0 恒成立,则 SKIPIF 1 < 0 的取值范围是______.
【题型训练】
一、单选题
1.已知集合 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 ( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0
C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
2.设函数 SKIPIF 1 < 0 则满足 SKIPIF 1 < 0 的 SKIPIF 1 < 0 取值范围是
A.[-1,2]B.[0,2]C.[1,+ SKIPIF 1 < 0 )D.[0,+ SKIPIF 1 < 0 )
3.若关于x的不等式 SKIPIF 1 < 0 有实数解,则实数a的取值范围是( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
4.若不等式 SKIPIF 1 < 0 恒成立,则实数 SKIPIF 1 < 0 的取值范围是( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
二、填空题
5. SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 ,则实数 SKIPIF 1 < 0 的取值范围为___________.
6.已知函数 SKIPIF 1 < 0 的图象关于原点对称,若 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 的取值范围为________.
三、解答题
7.解下列方程:
(1) SKIPIF 1 < 0 ; (2) SKIPIF 1 < 0 ;
(3) SKIPIF 1 < 0 ; (4) SKIPIF 1 < 0 .
8.已知函数 SKIPIF 1 < 0 ,与 SKIPIF 1 < 0 的图象关于直线 SKIPIF 1 < 0 对称的图象过点 SKIPIF 1 < 0 .
(1)求 SKIPIF 1 < 0 的值;
(2)求不等式 SKIPIF 1 < 0 的解集.
题型四 指数函数的综合应用
策略方法 指数函数通过平移、伸缩及翻折等变换,或与其他函数进行结合形成复合函数时,我们对这类问题的解决方式是进行还原分离,化繁为简,借助函数的单调性、奇偶性、对称性及周期性解决问题.
【典例1】函数 SKIPIF 1 < 0 单调递增区间为( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
【典例2】当 SKIPIF 1 < 0 时,不等式 SKIPIF 1 < 0 恒成立,则实数a的取值范围是( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
【典例3】已知 SKIPIF 1 < 0 是定义在 SKIPIF 1 < 0 上的奇函数,对任意正数 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,都有 SKIPIF 1 < 0 ,且 SKIPIF 1 < 0 ,当 SKIPIF 1 < 0 时, SKIPIF 1 < 0 ,则不等式 SKIPIF 1 < 0 的解集为( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0
C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
【题型训练】
一、单选题
1.函数 SKIPIF 1 < 0 ,下列关于函数 SKIPIF 1 < 0 的说法错误的是( )
A.函数 SKIPIF 1 < 0 的图象关于原点对称
B.函数 SKIPIF 1 < 0 的值域为 SKIPIF 1 < 0
C.不等式 SKIPIF 1 < 0 的解集是 SKIPIF 1 < 0
D. SKIPIF 1 < 0 是增函数
2.已知函数 SKIPIF 1 < 0 ,使不等式 SKIPIF 1 < 0 成立的一个必要不充分条件是( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 或 SKIPIF 1 < 0 C. SKIPIF 1 < 0 或 SKIPIF 1 < 0 D. SKIPIF 1 < 0 或 SKIPIF 1 < 0
3.已知 SKIPIF 1 < 0 为偶函数, SKIPIF 1 < 0 为奇函数,且满足 SKIPIF 1 < 0 .若对任意的 SKIPIF 1 < 0 都有不等式 SKIPIF 1 < 0 成立,则实数 SKIPIF 1 < 0 的最大值为( ).
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C.1D. SKIPIF 1 < 0
二、多选题
4.已知函数 SKIPIF 1 < 0 ,则( )
A.函数 SKIPIF 1 < 0 是增函数
B.曲线 SKIPIF 1 < 0 关于 SKIPIF 1 < 0 对称
C.函数 SKIPIF 1 < 0 的值域为 SKIPIF 1 < 0
D.曲线 SKIPIF 1 < 0 有且仅有两条斜率为 SKIPIF 1 < 0 的切线
5.已知函数 SKIPIF 1 < 0 ,对于任意的 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 ,关于 SKIPIF 1 < 0 的方程 SKIPIF 1 < 0 的解集可能的是( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
三、填空题
6.函数 SKIPIF 1 < 0 的单调减区间是_______.
7.求函数 SKIPIF 1 < 0 的单调区间___________.
8.已知函数 SKIPIF 1 < 0 为偶函数,则函数 SKIPIF 1 < 0 的值域为___________.
9. SKIPIF 1 < 0 ,其最大值和最小值的和为____________.
四、解答题
10.已知 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上的值域为 SKIPIF 1 < 0 .
(1)求实数 SKIPIF 1 < 0 的值;
(2)若不等式 SKIPIF 1 < 0 当 SKIPIF 1 < 0 上恒成立,求实数k的取值范围.
①指数幂的化简与求值
②指数函数的图像与性质
③解指数方程与不等式
④指数函数的综合应用
★【文末附录-指数运算和指数函数思维导图】
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
图象
性质
①定义域 SKIPIF 1 < 0 ,值域 SKIPIF 1 < 0
② SKIPIF 1 < 0 ,即时 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,图象都经过 SKIPIF 1 < 0 点
③ SKIPIF 1 < 0 ,即 SKIPIF 1 < 0 时, SKIPIF 1 < 0 等于底数 SKIPIF 1 < 0
④在定义域上是单调减函数
在定义域上是单调增函数
⑤ SKIPIF 1 < 0 时, SKIPIF 1 < 0 ; SKIPIF 1 < 0 时, SKIPIF 1 < 0
SKIPIF 1 < 0 时, SKIPIF 1 < 0 ; SKIPIF 1 < 0 时, SKIPIF 1 < 0
⑥既不是奇函数,也不是偶函数
新高考数学一轮复习讲义 第01讲 集合(2份打包,原卷版+含解析): 这是一份新高考数学一轮复习讲义 第01讲 集合(2份打包,原卷版+含解析),文件包含新高考数学一轮复习讲义第01讲集合原卷版doc、新高考数学一轮复习讲义第01讲集合含解析doc等2份试卷配套教学资源,其中试卷共46页, 欢迎下载使用。
新高考数学一轮复习导学案第12讲 指数与指数函数(2份打包,原卷版+解析版): 这是一份新高考数学一轮复习导学案第12讲 指数与指数函数(2份打包,原卷版+解析版),文件包含新高考一轮复习导学案第12讲指数与指数函数原卷版doc、新高考一轮复习导学案第12讲指数与指数函数解析版doc等2份试卷配套教学资源,其中试卷共19页, 欢迎下载使用。
新高考数学一轮复习讲义第10章 §10.2 排列与组合(2份打包,原卷版+含解析): 这是一份新高考数学一轮复习讲义第10章 §10.2 排列与组合(2份打包,原卷版+含解析),文件包含新高考数学一轮复习讲义第10章§102排列与组合原卷版doc、新高考数学一轮复习讲义第10章§102排列与组合含解析doc等2份试卷配套教学资源,其中试卷共19页, 欢迎下载使用。












