辽宁省朝阳市2023-2024学年八年级下学期期末数学试卷(含答案)

这是一份辽宁省朝阳市2023-2024学年八年级下学期期末数学试卷(含答案)，共19页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。


一、单选题
1．剪纸是中国最古老的民间艺术之一,先后入选中国国家级非物质文化遗产名录和人类非物质文化遗产代表作名录.下列剪纸作品中是中心对称图形但不是轴对称图形的是( )
A.B.
C.D.
2．不等式的解集在数轴上表示正确的是( )
A.B.
C.D.
3．如图,为测量位于一水塘旁的两点A,B间的距离,在地面上确定点O,分别取,的中点C,D,量得,则A,B之间的距离是( )
A.B.C.D.
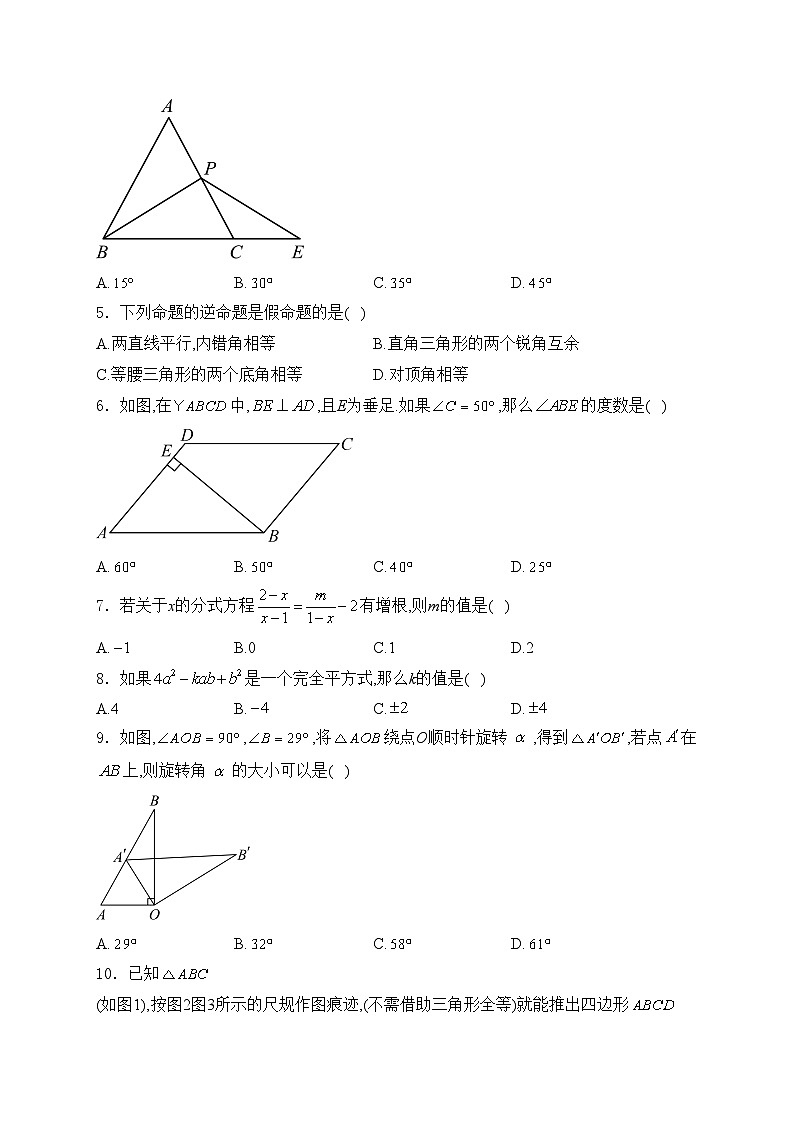
4．如图,P是等边三角形的边的中点,E是边延长线上一点,,则的度数是( )
A.B.C.D.
5．下列命题的逆命题是假命题的是( )
A.两直线平行,内错角相等B.直角三角形的两个锐角互余
C.等腰三角形的两个底角相等D.对顶角相等
6．如图,在中,,且E为垂足.如果,那么的度数是( )
A.B.C.D.
7．若关于x的分式方程有增根,则m的值是( )
A.B.0C.1D.2
8．如果是一个完全平方式,那么k的值是( )
A.4B.C.D.
9．如图,,,将绕点O顺时针旋转,得到,若点在上,则旋转角的大小可以是( )
A.B.C.D.
10．已知(如图1),按图2图3所示的尺规作图痕迹,(不需借助三角形全等)就能推出四边形是平行四边形的依据是( )
A.两组对边分别平行的四边形是平行四边形
B.一组对边平行且相等的四边形是平行四边形
C.对角线互相平分的四边形是平行四边形
D.两组对边分别相等的四边形是平行四边形
二、填空题
11．因式分解：______.
12．当______时,分式的值为零.
13．如图,以点O为圆心,任意长为半径作弧分别交,于C,D两点,分别以点C,D为圆心,以大于的长为半径作弧,两弧相交于点P,以O为端点作射线,在射线上截取线段,则点M到的距离为______.
14．若一个多边形的内角和是外角和的2倍,则这个多边形的边数为______.
15．如图,直线与轴交于点A,直线与轴交于点B,与y轴交于点C,与直线交于点D,点P为直线上一动点,当的面积为四边形面积的时,点P的坐标为______.
三、解答题
16．(1)解不等式组：；
(2)解分式方程：.
17．先化简,再求值：,其中.
18．如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,的顶点均在格点上,点C的坐标为.
(1)把向左平移4个单位后得到对应的,请画出平移后的,并写出点的坐标；
(2)把绕原点O顺时针旋转后得到对应的,请画出旋转后的,并写出点的坐标.
19．暑热已至,烈日炎炎,中小学生野浴行为增多,溺水事故进入高发期.据统计我国每年约有5.9万人死于溺水,其中未成年人占以上.为了让孩子们安全健康的快乐成长,某校要制作一批防溺水安全工作的宣传材料发放给学生和家长.现有甲乙两家印刷厂可供选择,甲印刷厂提出：每份材料收费1.5元；另收300元的版面设计费；乙印刷厂提出：每份材料收费2元,不收版面设计费.请你帮助该学校选择制作方案,使得支付的印刷费用较少.
20．已知,如图,在四边形中,,过点A作于点E,.
(1)求证：；
(2)若点D恰好在线段的垂直平分线上,,,求线段的长.
21．【阅读材料】数学教科书中这样写道：“形如的式子称为完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形：先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变.这是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式的最大值,最小值等.
例1：分解因式：.
解：.
例2：求代数式的最小值：
解：.可知当时,有最小值,最小值是.
请根据阅读材料中的方法解决下列问题：
(1)将多项式因式分解；
(2)求多项式的最小值.
22．某商场用1200元购进一批新型乳制品,面市后深受消费者喜欢,很快销售完,又用4800元购进第二批这种乳制品,所购数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批乳制品的进货单价为多少元？
(2)若两次购进乳制品按同一价格销售,两批全部售完后,获利不少于1200元,则销售单价至少为多少元？
23．【问题背景】
某数学兴趣小组在学习了平行四边形后,对其进行了轴对称变换的操作,进一步研究平行四边形的性质.在中,,,,点E是边上任意一点,连接,将四边形沿翻折得到四边形,射线与相交于点F.
【操作发现】
(1)如图1,无论点E在什么位置,图中都会有一条线段与相等,请猜想与相等的线段,并说明理由.
【问题延伸】
(2)当点E的位置发生变化时,线段存在最小值,请求出线段的最小值.
【问题拓展】
(3)如图2,连接,当是以为一条直角边的直角三角形时,求线段的长.
参考答案
1．答案：C
解析：A.该图形是轴对称图形,不是中心对称图形,故A选项不符合题意；
B.该图形既是轴对称图形,又是中心对称图形,故B选项不符合题意；
C.该图形不是轴对称图形,是中心对称图形,故C选项符合题意；
D.该图形不是轴对称图形,也不是中心对称图形,故D选项不符合题意.
故选：C.
2．答案：C
解析：在数轴上表示时,其点应是空心,方向为向右,
因此,综合各选项,只有C选项符合；
故选：C.
3．答案：B
解析：∵C,D是,的中点,
∴是的中位线,
∴,
故选：B.
4．答案：B
解析：∵P是等边三角形的边的中点,
∴平分,,
∴,
∵,
∴,
∴,
故选：B.
5．答案：D
解析：A.两直线平行,内错角相等,逆命题是内错角相等,两直线平行,故选项的逆命题是真命题,不符合题意；
B.直角三角形的两个锐角互余的逆命题是有两个内角互余的三角形是直角三角形,故选项的逆命题是真命题,不符合题意；
C.等腰三角形的两个底角相等的逆命题是有两个角相等的三角形是等腰三角形,故选项的逆命题是真命题,不符合题意；
D.对顶角相等的逆命题是相等的角是对顶角,故选项的逆命题是假命题,符合题意.
故选：D.
6．答案：C
解析：在中,,
∴,
∵,且E为垂足.
∴
∴,
故选：C.
7．答案：A
解析：∵分式方程有增根,
∴,
原方程去分母可得：,
把代入可得：,
解得：.
故选：A.
8．答案：D
解析：∵是一个完全平方式,
∴,
∴.
故选：D.
9．答案：C
解析：∵,,
∴,
根据旋转的性质得到,
∴,
∴,
即则旋转角的大小可以是,
故选：C
10．答案：C
解析：由图可知先作AC的垂直平分线,则点O为AC的中点,由作图可知,
可得：,,
进而得出四边形ABCD是平行四边形,
故选：C.
11．答案：
解析：,
故答案为：.
12．答案：1
解析：∵分式的值为零,
∴,
解得：,
∴；
故答案为：1.
13．答案：4
解析：过点M作于点E,
由题意可得：是的角平分线,
则,
∴.
则点M到的距离为4,
故答案为：4
14．答案：6/六
解析：设多边形的边数为n,
依题意得,,
解得,,
故答案为：6.
15．答案：或
解析：在中,令,则,
,
在中,令,则,当,则,
,
∴,
解,得,
,
,,
；
P在上方时,过点P作交x轴于点M,连接,如图：
,
,
的面积是四边形的面积的,
,
,即,
,
,
,
设直线为：,
将代入得：,
,
直线为：,
解,得,
,
当P在下方时,过点作交x轴于点,如图：
,
,
的面积是四边形的面积的,
,
,即,
,
,
,
设直线为：,
将代入得：,
,
直线为：,
解,得,
,
综上所述,P得坐标为或.
故答案为：或
16．答案：(1)
(2)
解析：(1)
解不等式①得,
解不等式②得,
∴原不等式组的解集是
(2)
两边同乘以得,,
解方程得,,
当时,,
∴是分式方程的解
17．答案：,
解析：
当时,
原式
18．答案：(1)图见解析,
(2)图见解析,
解析：(1)如图所示,即为所求,点的坐标为；
(2)如图所示,即为所求,点的坐标为.
19．答案：当材料份数大于600时,选甲合适；当材料份数小于600时,选乙合适
解析：设要做的材料为x份.
第一种情况：当,解得,
所以当材料份数大于600时,选甲合适；
第二种情况：当,解得,
所以当材料份数小于600时,选乙合适.
20．答案：(1)证明见解析
(2)
解析：(1)∵,过点A作于点E,
又.
∴,
∴；
(2)∵
∴,
设,则,
∵点D恰好在线段的垂直平分线上,
∴,
∵于点E,
∴,
∴,
即,
解得
即线段的长为.
21．答案：(1)
(2)
解析：(1)
,
,
；
(2)
,
,
∵,
∴当时,有最小值,最小值是.
22．答案：(1)第一批乳制品的进货单价为6元
(2)销售单价至少为9元
解析：(1)设第一批乳制品的进货单价为x元,则第二批乳制品的进货单价为元,则
解得,
经检验是分式方程的解且符合题意,
答：第一批乳制品的进货单价为6元；
(2)设销售单价为m元,则
,
解得
答：销售单价至少为9元.
23．答案：(1),理由见解析
(2)
(3)线段的长为或或
解析：(1),理由如下,
情况①,当射线与相交于点F,点F在线段上,如图,
四边形是平行四边形,
,
,
将四边形沿翻折得到四边形,
根据翻折特征,得,
,
.
情况②当射线与相交于点F,点F在线段延长线上,如图,
同理可得,,
.
情况③当点E在如图位置,延长线与相交于点F,
四边形是平行四边形,
,
将四边形沿翻折得到四边形,
根据翻折特征,得,,
,
,
.
综上,无论点E在什么位置,都有.
(2),根据垂线段最短,
当时,最短,故此时取得最小值,如图所示,
,,,
根据勾股定理得,,
线段的最小值为.
(3)情况①当时,,是以为一条直角边的直角三角形,如图所示,
四边形是平行四边形,
,,
将四边形沿翻折得到四边形,
根据翻折特征,得,
,
,即,
是以为一条直角边的直角三角形,
根据第(2)结果,,
.
情况②,,是以为一条直角边的直角三角形,如图所示,
四边形是平行四边形,
,,,,
将四边形沿翻折得到四边形,
根据翻折特征,得,,,,,
,,
,
是等腰直角三角形,
根据勾股定理得,,
,
,
在中,,
.
情况③当点E与点B重合时,即将四边形沿翻折得到四边形,
,根据翻折特征,可得,
,
是以为一条直角边的直角三角形,
此时,.
综上,当是以为一条直角边的直角三角形,线段的长为或或.