2023-2024学年山东省德州市禹城市八年级（下）期末数学试卷（含详细答案解析）

这是一份2023-2024学年山东省德州市禹城市八年级（下）期末数学试卷（含详细答案解析），共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.下列二次根式中，是最简二次根式的是( )
A. 12B. 15C. 27D. 52
2.△ABC中，∠A，∠B，∠C的对边分别记为a，b，c，下列条件不能判定△ABC为直角三角形的是( )
A. ∠A+∠B=∠CB. ∠A：∠B：∠C=1：2：3
C. a2=c2−b2D. a：b：c= 3： 4： 5
3.某射击小组有20人，教练根据他们某次射击的数据绘制成如图所示的统计图，则这组数据的众数和中位数分别是( )
A. 7，7B. 8，7.5C. 8，6.5D. 7，7.5
4.下列有关一次函数y=−3x+2的说法中，错误的是( )
A. y的值随着x值的增大而减小B. 函数图象与x轴的交点坐标为(0,2)
C. 当x2D. 函数图象经过第一、二、四象限
5.如图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．若AC=6，BC=5，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到图2所示的“数学风车”，则这个风车的外围周长是( )
A. 72B. 52C. 80D. 76
6.已知点P(−1,y1)、点Q(3,y2)在一次函数y=(2m−1)x+2的图象上，且y1>y2，则m的取值范围是( )
A. m12C. m≥1D. m−3，
∵−kx−b0，
∴−kx−b−3.
故选：A.
9.【答案】C
【解析】解：∵四边形ABCD是菱形，
∴OA=OC，OB=OD=12BD，BD⊥AC，
∴BD=16，
∵S菱形ABCD=12AC×BD=96，
∴AC=12，
∵CE⊥AD，
∴∠AEC=90∘，
∴OE=12AC=6，
故选：C.
由菱形的性质得出BD=16，由菱形的面积得出AC=12，再由直角三角形斜边上的中线性质即可得出结果．
此题主要考查了菱形的性质、直角三角形斜边上的中线性质；熟练掌握菱形的性质是解题的关键．
10.【答案】D
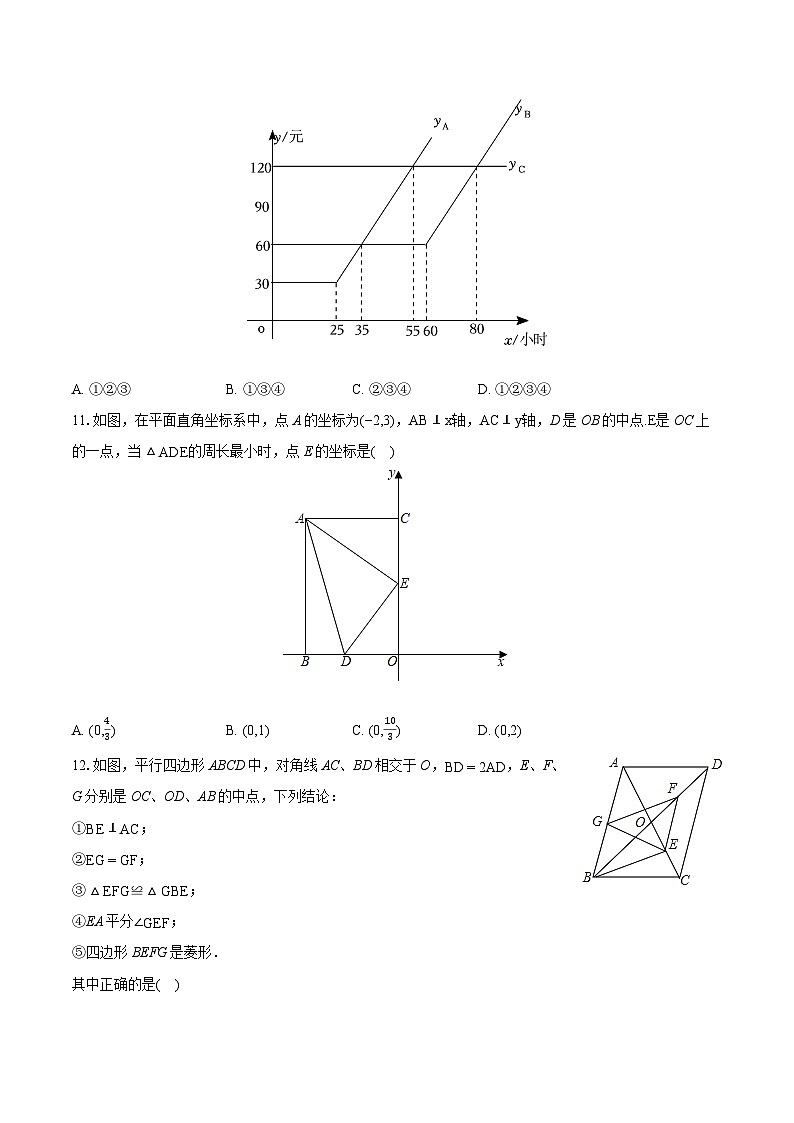
【解析】解：由图象可知：①月上网时间不足35小时，选择方式A最省钱，说法正确；
②月上网时间超过35小时且不足80小时，选择方式B最省钱，说法正确；
③对于上网方式B，若月上网时间在60小时以内，则月收费金额为60元，说法正确；
④对于上网方式C，无论月上网时间是多久，月收费都是120元，说法正确，
所以所有合理推断的序号是①②③④．
故选：D.
根据A，B，C三种上宽带网方式的月收费金额yA(元)，yB(元)，yC(元)与月上网时间x(小时)的图象逐一进行判断即可．
本题考查了函数的图象，掌握数形结合的方法是解答本题的关键．
11.【答案】B
【解析】解：作点A关于y轴的对称点A′，连接A′D，
此时△ADE的周长最小值为AD+DA′的长，
∵AB⊥x轴，AC⊥y轴，x轴⊥y轴，A的坐标为(−2,3)，
∴C(0,3)，AC//x轴，AB//y轴，
∴AC=OB=2，
∵D是OB的中点，
∴D(−1,0)，
由对称可知A′(2,3)，
设A′D的直线解析式为y=kx+b，
则：2k+b=3−k+b=0，
解得：k=1b=1，
∴y=x+1，
当x=0时，y=1，
∴E(0,1).
故选：B.
作点A关于y轴的对称点A′，连接A′D，此时△ADE的周长最小值为AD+DA′的长；E点坐标即为直线A′D与y轴的交点．
本题考查坐标与图形的性质，轴对称-路线最短问题．能够利用轴对称求线段的最短距离，将AE+DE的最短距离转化为线段A′D的长是解题的关键．
12.【答案】B
【解析】解：∵四边形ABCD是平行四边形
∴BO=DO=12BD，AD=BC，AB=CD，AB//BC，
又∵BD=2AD，
∴OB=BC=OD=DA，且点E 是OC中点，
∴BE⊥AC，
故①正确；
∵E、F分别是OC、OD的中点，
∴EF//CD，EF=12CD，
∵点G是Rt△ABE斜边AB上的中点，
∴GE=12AB=AG=BG
∴EG=EF=AG=BG，无法证明GE=GF，
故②错误；
∵BG=EF，AB//CD//EF，
∴四边形BGFE是平行四边形，
∴GF=BE，且BG=EF，GE=GE，
∴△BGE≌△FEG(SSS)
故③正确；
∵EF//CD//AB，
∴∠BAC=∠ACD=∠AEF，
∵AG=GE，
∴∠GAE=∠AEG，
∴∠AEG=∠AEF，
∴AE平分∠GEF，
故④正确，
若四边形BEFG是菱形
∴BE=BG=12AB，
∴∠BAC=30∘
与题意不符合
故⑤错误，
故选：B.
根据平行四边形的性质可得OB=BC，由等腰三角形的性质可判断①正确，由直角三角形的性质和三角形中位线定理可判断②错误，通过证四边形BGFE是平行四边形，可判断③正确，由平行线的性质和等腰三角形的性质可判断④正确，由∠BAC≠30∘可判断⑤错误．
本题考查了菱形的判定，平行四边形的性质，全等三角形的判定和性质，三角形中位线定理等知识，灵活运用相关的性质定理、综合运用知识是解题的关键．
13.【答案】−3≤x1
【解析】解：由代数式 x+3x−1有意义，得
x+3≥0x−1≠0.
解得−3≤x1，
故答案为：−3≤x1.
根据函数表达式是分式时，考虑分式的分母不能为0；函数表达式是二次根式时，被开方数非负，可得答案．
本题考查了二次根式有意义的条件，函数自变量的范围一般从三个方面考虑：当函数表达式是整式时，自变量可取全体实数；当函数表达式是分式时，考虑分式的分母不能为0；当函数表达式是二次根式时，被开方数非负．
14.【答案】89
【解析】解：80×3+90×3+95×43+3+4=89(分)，
即他本学期数学学期综合成绩是89分．
故答案为：89.
根据加权平均数的定义列式计算即可．
本题主要考查加权平均数，解题的关键是掌握加权平均数的定义．
15.【答案】125
【解析】解：∵四边形ABCD是菱形，
∴AC⊥BD，OA=OC=12AC=12×8=4，OB=OD=12BD=12×6=3，
在Rt△AOB中，AB= OA2+OB2= 42+32=5，
如图所示，连接OP，
∵PE⊥OA于点E，PF⊥OB于点F，
∴四边形OEPF是矩形，则EF=OP，
当OP⊥AB时，OP的值最小，即EF的值最小，
∴S△AOB=12OA⋅OB=12AB⋅OP，
∴OP=OA⋅OBAB=4×35=125，
∴EF的最小值为125，
故答案为：125.
根据菱形的性质，可证四边形OEPF是矩形，如图所示，连接OP，则EF=OP，当OP⊥AB时，OP的值最小，即EF的值最小，再根据等面积法求高即可求解．
本题主要考查菱形的性质、矩形的判定与性质、勾股定理及垂线段最短，掌握菱形，矩形的性质，等面积法求三角形的高的计算方法是解题的关键．
16.【答案】x=1y=2
【解析】解：把x=1代入y=x+1，得出y=2，
函数y=x+1和y=ax+3的图象交于点P(1,2)，
即x=1，y=2同时满足两个一次函数的解析式．
所以关于x，y的方程组y=x+1y=ax+3的解是x=1y=2.
故答案为x=1y=2.
先把x=1代入y=x+1，得出y=2，则两个一次函数的交点P的坐标为(1,2)；那么交点坐标同时满足两个函数的解析式，而所求的方程组正好是由两个函数的解析式所构成，因此两函数的交点坐标即为方程组的解．
考查了一次函数与二元一次方程组的联系，方程组的解就是使方程组中两个方程同时成立的一对未知数的值，而这一对未知数的值也同时满足两个相应的一次函数式，因此方程组的解就是两个相应的一次函数图象的交点坐标．
17.【答案】360
【解析】解：设甲的速度为v1米/分钟，乙的速度为v2米/分钟，
∴v1=2404=60米/分钟，
由图象可知：乙追上甲需要12分钟，
∴12v2=240+12×60，
∴v2=80米/分钟，
∴此时乙共走了12×80=960米，
∴乙离终点还有2400−960=1440米，
∴乙到达终点时需要的时间为：144080=18分钟，
∴甲离终点还有1440−18×60=360米，
故答案为：360.
设甲的速度为v1米/分钟，乙的速度为v2米/分钟，根据图象的信息科求出甲乙两人的速度，以及相遇所需要的时间，从而可求出答案．
本题考查函数图象的应用，解题的关键是正确理解图象并求出甲乙两人的速度，本题属于中等题型．
18.【答案】13
【解析】【分析】
本题考查了三角形中位线定理、勾股定理、平行线的性质等知识；熟练掌握三角形中位线定理和勾股定理，正确作出辅助线是解题的关键．
连接BD，取BD的中点F，连接MF、NF，证明NF、MF分别是△BDE、△ABD的中位线，由三角形中位线定理得出NF//BE，MF//AD，NF=12BE=5，MF=12AD=12，证出NF⊥MF，在Rt△MNF中，由勾股定理即可得出答案．
【解答】
解：连接BD，取BD的中点F，连接MF、NF，如图所示：
∵M、N、F分别是AB、DE、BD的中点，
∴NF、MF分别是△BDE、△ABD的中位线，
∴NF//BE，MF//AD，NF=12BE=5，MF=12AD=12，
∵∠ACB=90∘，
∴AD⊥BC，
∵MF//AD，
∴MF⊥BC，
∵NF//BE，
∴NF⊥MF，
在Rt△MNF中，由勾股定理得：MN= NF2+MF2= 52+122=13；
故答案为：13.
19.【答案】解：(1)原式=12−4 3+1+3−5 3+2 3−10
=6−7 3；
(2)原式=( 3× 3× 2−2 2+ 3)×( 3− 2)
=(3 2−2 2+ 3)×( 3− 2)
=( 3+ 2)×( 3− 2)
=( 3)2−( 2)2
=3−2
=1.
【解析】(1)先根据完全平方公式和多项式乘法法则运算，然后合并即可；
(2)线利用二次根式的乘法法则运算，再分母有理化和去绝对值，然后合并同类二次根式后利用平方差公式计算．
本题考查了二次根式的混合运算：熟练掌握二次根式的性质、二次根式的乘法法则、除法法则是解决问题的关键．
20.【答案】解：(1)85， 85 ，80；
(2)小学部成绩好些．
因为两个队的平均数都相同，小学部的中位数高，
所以在平均数相同的情况下中位数高的小学部成绩好些．
(3)∵s12=(75−85)2+(80−85)2+(85−85)2+(85−85)2+(100−85)25=70，s22=(70−85)2+(100−85)2+(100−85)2+(75−85)2+(80−85)25=160，
∴s1250)，
综上，y=25x(0≤x≤50)20x+250(x>50)；
(2)∵购进A种图书x本，则购进B种图书(300−x)本，
根据题意得，x≥60x≤2(300−x)，
∴解得60≤x≤200，
∴购进两种图书的总费用w=20x+250+22(300−x)=−2x+6850，
∵−2