

2025高考数学一轮复习-7.2-空间点、直线、平面之间的位置关系-专项训练【含解析】
展开
这是一份2025高考数学一轮复习-7.2-空间点、直线、平面之间的位置关系-专项训练【含解析】,共9页。试卷主要包含了下列四个命题中是真命题的为等内容,欢迎下载使用。
1.如图,α∩β=l,A,B∈α,C∈β,且C∉l,直线AB∩l=M,过A,B,C三点的平面记作γ,则γ与β的交线必通过( )
A.点A B.点B
C.点C但不过点MD.点C和点M
2.若a∥α,b∥β,α∥β,则a,b的位置关系是( )
A.平行B.异面
C.相交D.平行或异面或相交
3.已知a,b,c是三条不同的直线,α,β是两个不同的平面,α∩β=c,a⊂α,b⊂β,则“a,b相交”是“a,c相交”的( )
A.充要条件B.必要不充分条件
C.充分不必要条件D.既不充分也不必要条件
4.过长方体的一个顶点的平面与这个长方体的十二条棱所在的直线成的角都相等,这样的平面个数为( )
A.4B.1
C.0D.无数多个
5.(多选)下列四个命题中是真命题的为( )
A.两两相交且不过同一点的三条直线必在同一平面内
B.过空间中任意三点有且仅有一个平面
C.若空间两条直线不相交,则这两条直线平行
D.若直线l⊂平面α,直线m⊥平面α,则m⊥l
6.(多选)如图,点E,F,G,H分别是正方体ABCDA1B1C1D1中棱AA1,AB,BC,C1D1的中点,则( )
A.GH=2EF
B.GH≠2EF
C.直线EF,GH是异面直线
D.直线EF,GH是相交直线
7.如图,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,则直线EF与正方体的六个面所在的平面相交的平面个数为________.
8.如图,已知圆柱的轴截面ABB1A1是正方形,C是圆柱下底面弧AB的中点,C1是圆柱上底面弧A1B1的中点,那么异面直线AC1与BC所成角的正切值为________.
9.在棱长为4的正方体ABCDA1B1C1D1中,E,F分别是BC和C1D1的中点,经过点A,E,F的平面把正方体ABCDA1B1C1D1截成两部分,求截面与BCC1B1的交线段长.
10.已知正方体ABCDA1B1C1D1的棱长为3eq \r(2),E,F分别为BC,CD的中点,P是线段A1B上的动点,C1P与平面D1EF的交点Q的轨迹长为( )
A.3B.eq \r(13)
C.4D.3eq \r(2)
11.(多选)如图所示,在正方体ABCDA1B1C1D1中,O是B1D1的中点,直线A1C交平面AB1D1于点M,则下列结论正确的是( )
A.A,M,O三点共线B.A,M,O,A1共面
C.A,M,C,O共面D.B,B1,O,M共面
12.空间三条直线a,b,c两两异面,则与三条直线都相交的直线有________条.
13.如图,AB,CD是圆锥面的正截面(垂直于轴的截面)上互相垂直的两条直径,过CD和母线VB的中点E作一截面.已知圆锥侧面展开图扇形的中心角为eq \r(2)π,求截面与圆锥的轴线所夹的角的大小,并说明截线是什么曲线.
.
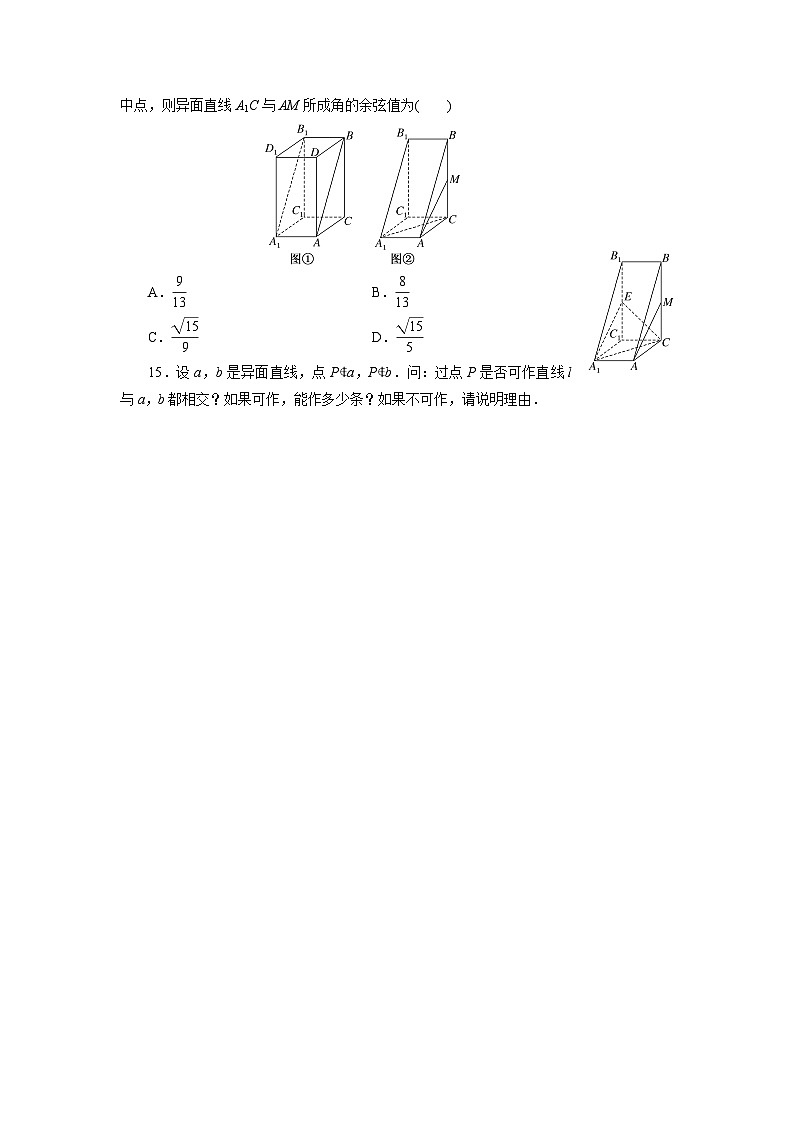
14.《九章算术·商功》中刘徽注:“邪解立方得二堑堵,邪解堑堵,其一为阳马,其一为鳖臑.”如图①所示的长方体用平面AA1B1B斜切一分为二,得到两个一模一样的三棱柱,该三棱柱就叫堑堵.如图②所示的堑堵中,AC=3,BC=4,AB=5,AA1=2,M为BC的中点,则异面直线A1C与AM所成角的余弦值为( )
A.eq \f(9,13)B.eq \f(8,13)
C.eq \f(\r(15),9)D.eq \f(\r(15),5)
15.设a,b是异面直线,点P∉a,P∉b.问:过点P是否可作直线l与a,b都相交?如果可作,能作多少条?如果不可作,请说明理由.
2025高考数学一轮复习-7.2-空间点、直线、平面之间的位置关系-专项训练【解析版】
1.如图,α∩β=l,A,B∈α,C∈β,且C∉l,直线AB∩l=M,过A,B,C三点的平面记作γ,则γ与β的交线必通过( )
A.点A B.点B
C.点C但不过点MD.点C和点M
解析:D ∵AB⊂γ,M∈AB,∴M∈γ.又α∩β=l,M∈l,∴M∈β.根据基本事实3可知,M在γ与β的交线上.同理可知,点C也在γ与β的交线上.
2.若a∥α,b∥β,α∥β,则a,b的位置关系是( )
A.平行B.异面
C.相交D.平行或异面或相交
解析:D 如图①②③所示,a,b的关系分别是平行、异面、相交.
3.已知a,b,c是三条不同的直线,α,β是两个不同的平面,α∩β=c,a⊂α,b⊂β,则“a,b相交”是“a,c相交”的( )
A.充要条件B.必要不充分条件
C.充分不必要条件D.既不充分也不必要条件
解析:C 若a,b相交,a⊂α,b⊂β,则其交点在交线c上,故a,c相交;若a,c相交,可能a,b为相交直线或异面直线.综上所述:a,b相交是a,c相交的充分不必要条件.故选C.
4.过长方体的一个顶点的平面与这个长方体的十二条棱所在的直线成的角都相等,这样的平面个数为( )
A.4B.1
C.0D.无数多个
解析:A 由题意,题目中的长方体与正方体,所作的平面个数相同,所以用正方体代替长方体来求解.
法一:在正方体ABCDA1B1C1D1中,三棱锥AA1BD是正三棱锥,直线AB,AD,AA1与平面A1BD所成角都相等,过顶点A作平面α∥平面A1BD,则直线AB,AD,AA1与平面α所成角都相等,同理,过顶点A分别作平面α与平面C1BD、平面B1AC,平面D1AC平行,直线AB、AD、AA1与平面α形成的角都相等,因此符合条件的平面可作4个,故选A.
法二:只要与体对角线垂直的平面都和正方体的所有棱所成的角相等,因为有四条体对角线,所以,可以做4个平面.故选A.
5.(多选)下列四个命题中是真命题的为( )
A.两两相交且不过同一点的三条直线必在同一平面内
B.过空间中任意三点有且仅有一个平面
C.若空间两条直线不相交,则这两条直线平行
D.若直线l⊂平面α,直线m⊥平面α,则m⊥l
解析:AD 对于A,可设l1与l2相交,这两条直线确定的平面为α;若l3与l1相交,则交点A在平面α内,同理,l3与l2的交点B也在平面α内,所以,AB⊂α,即l3⊂α,A为真命题;
对于B,若三点共线,则过这三个点的平面有无数个,故B为假命题;
对于C,两条直线有可能平行也有可能异面,故C为假命题;
对于D,若直线m⊥平面α,则m垂直于平面α内所有直线,因为直线l⊂平面α,所以直线m⊥直线l,D为真命题.
6.(多选)如图,点E,F,G,H分别是正方体ABCDA1B1C1D1中棱AA1,AB,BC,C1D1的中点,则( )
A.GH=2EF
B.GH≠2EF
C.直线EF,GH是异面直线
D.直线EF,GH是相交直线
解析:BD 如图,取棱CC1的中点N,A1D1的中点M,连接EM,MH,HN,NG,FG,AC,A1C1,在正方体ABCDA1B1C1D1中,∵MH∥A1C1∥AC∥FG,∴M,H,F,G四点共面,同理可得E,M,G,N四点共面,E,F,H,N四点共面,∴E,M,H,N,G,F六点共面,均在平面EFGNHM内,∵EF∥HN,HN∩HG=H,HN,HG,EF⊂平面EFGNHM,∴EF与GH是相交直线.由正方体的结构特征及中位线定理可得EF=HN=NG=FG=EM=MH,∴eq \r(3)EF=GH,即GH≠2EF.故选B、D.
7.如图,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,则直线EF与正方体的六个面所在的平面相交的平面个数为________.
解析:因为AB∥CD,由图可以看出EF平行于正方体左右两个侧面,与另外四个侧面相交.
答案:4
8.如图,已知圆柱的轴截面ABB1A1是正方形,C是圆柱下底面弧AB的中点,C1是圆柱上底面弧A1B1的中点,那么异面直线AC1与BC所成角的正切值为________.
解析:如图,取圆柱下底面弧AB的另一中点D,连接C1D,AD,因为C是圆柱下底面弧AB的中点,所以AD∥BC,
所以直线AC1与AD所成角等于异面直线AC1与BC所成角.因为C1是圆柱上底面弧A1B1的中点,所以C1D⊥圆柱下底面,所以C1D⊥AD,因为圆柱的轴截面ABB1A1是正方形,所以C1D=eq \r(2)AD,所以直线AC1与AD所成角的正切值为eq \r(2),所以异面直线AC1与BC所成角的正切值为eq \r(2).
答案:eq \r(2)
9.在棱长为4的正方体ABCDA1B1C1D1中,E,F分别是BC和C1D1的中点,经过点A,E,F的平面把正方体ABCDA1B1C1D1截成两部分,求截面与BCC1B1的交线段长.
解:如图,连接AE并延长交DC的延长线于M,连接FM交CC1于G,连接EG并延长交B1C1的延长线于N,连接NF并延长交A1D1于H,连接AH,则五边形AEGFH为经过点A,E,F的正方体的截面,
因为E为BC的中点,所以CE=eq \f(1,2)BC=2,
因为CE∥AD,所以△MCE∽△MDA,
所以eq \f(CM,DM)=eq \f(CE,AD)=eq \f(1,2),所以CM=CD=4,
因为DM∥C1D1,所以△MCG∽△FC1G,
所以eq \f(CG,C1G)=eq \f(CM,C1F)=2,所以CG=eq \f(2,3)×4=eq \f(8,3),
所以EG=eq \r(CE2+CG2)=eq \r(22+\b\lc\(\rc\)(\a\vs4\al\c1(\f(8,3)))2)=eq \f(10,3),
所以截面与BCC1B1的交线段长为eq \f(10,3).
10.已知正方体ABCDA1B1C1D1的棱长为3eq \r(2),E,F分别为BC,CD的中点,P是线段A1B上的动点,C1P与平面D1EF的交点Q的轨迹长为( )
A.3B.eq \r(13)
C.4D.3eq \r(2)
解析:B 如图所示,连接EF,A1B,连接A1C1,B1D1交于点M,连接B1E,BC1交于点N,连接MN,由EF∥B1D1,得E,F,B1,D1共面,由P是线段A1B上的动点,当P重合于A1或B时,C1A1,C1B与平面D1EF的交点分别为M,N,即Q的轨迹为MN,由棱长为3eq \r(2),得C1M=eq \f(1,2)A1C1=3, 则BC1=6,又eq \f(BE,B1C1)=eq \f(BN,NC1)=eq \f(1,2),则NC1=eq \f(2,3)BC1=4,由A1B=BC1=A1C1,得∠A1C1B=60°,则MN=eq \r(MC\\al(2,1)+NC\\al(2,1)-2MC1·NC1·cs∠A1C1B)=eq \r(9+16-2×3×4×\f(1,2))=eq \r(13).
11.(多选)如图所示,在正方体ABCDA1B1C1D1中,O是B1D1的中点,直线A1C交平面AB1D1于点M,则下列结论正确的是( )
A.A,M,O三点共线B.A,M,O,A1共面
C.A,M,C,O共面D.B,B1,O,M共面
解析:ABC ∵M∈A1C,A1C⊂平面A1ACC1,∴M∈平面A1ACC1,又∵M∈平面AB1D1,∴M在平面AB1D1与平面A1ACC1的交线AO上,即A,M,O三点共线,∴A,M,O,A1共面且A,M,C,O共面,∵平面BB1D1D∩平面AB1D1=B1D1,∴M在平面BB1D1D外,即B,B1,O,M不共面,故选A、B、C.
12.空间三条直线a,b,c两两异面,则与三条直线都相交的直线有________条.
解析:取a,b,c为一正方体三条两两异面的棱AD,CC1,A1B1,在AD上任取一点M,在BC上取点N,使得B1N∥A1M,设直线B1N与CC1交于点P,PM即与a,b,c都相交,由于M是任取的,故满足条件的直线有无数条.
答案:无数
13.如图,AB,CD是圆锥面的正截面(垂直于轴的截面)上互相垂直的两条直径,过CD和母线VB的中点E作一截面.已知圆锥侧面展开图扇形的中心角为eq \r(2)π,求截面与圆锥的轴线所夹的角的大小,并说明截线是什么曲线.
解:如图,设⊙O的半径为R,母线VB=l,则圆锥侧面展开图的中心角为eq \f(2πR,l)=eq \r(2)π,∴eq \f(R,l)=eq \f(\r(2),2),
∴sin∠BVO=eq \f(\r(2),2),
∴圆锥的母线与轴的夹角α=∠BVO=eq \f(π,4).
连接OE,∵O,E分别是AB,VB的中点,
∴OE∥VA.
∴∠VOE=∠AVO=∠BVO=eq \f(π,4),
∴∠VEO=eq \f(π,2),即VE⊥OE.
又∵AB⊥CD,VO⊥CD,AB∩VO=O,
∴CD⊥平面VAB.
∵VE⊂平面VAB,
∴VE⊥CD.
又∵OE∩CD=O,OE,CD⊂平面CDE,
∴VE⊥平面CDE.
∴∠VOE是截面与轴线的夹角,
∴截面的轴线夹角大小为eq \f(π,4).
由圆锥的半顶角与截面与轴线的夹角相等,知截面CDE与圆锥面的截线为一抛物线.
14.《九章算术·商功》中刘徽注:“邪解立方得二堑堵,邪解堑堵,其一为阳马,其一为鳖臑.”如图①所示的长方体用平面AA1B1B斜切一分为二,得到两个一模一样的三棱柱,该三棱柱就叫堑堵.如图②所示的堑堵中,AC=3,BC=4,AB=5,AA1=2,M为BC的中点,则异面直线A1C与AM所成角的余弦值为( )
A.eq \f(9,13)B.eq \f(8,13)
C.eq \f(\r(15),9)D.eq \f(\r(15),5)
解析:A 如图,取B1C1的中点E,连接A1E,EC,则A1E∥AM,∠EA1C即为异面直线A1C与AM所成的角或其补角,在Rt△A1C1E中,A1E=eq \r(9+4)=eq \r(13),在Rt△EC1C中,EC=eq \r(22+22)=2eq \r(2),在Rt△A1C1C中,A1C=eq \r(13),在△A1EC中,由余弦定理得,cs∠EA1C=eq \f(A1E2+A1C2-EC2,2A1E·A1C)=eq \f(13+13-8,2×\r(13)×\r(13))=eq \f(9,13),故异面直线A1C与AM所成角的余弦值为eq \f(9,13),故选A.
15.设a,b是异面直线,点P∉a,P∉b.问:过点P是否可作直线l与a,b都相交?如果可作,能作多少条?如果不可作,请说明理由.
解:因为P∉a,P∉b,所以点P与直线a,b分别可确定一个平面α,β.又平面α,β有一个公共点P,所以它们有且只有一条经过点P的直线l.
(1)当l∥\a,且l∥\b时,l就是合乎要求的直线,且唯一;
(2)当l∥a,或l∥b时,这样的直线不存在.
相关试卷
这是一份2025年高考数学一轮复习-7.2-空间点、直线、平面之间的位置关系-专项训练【含答案】,共5页。
这是一份2025高考数学一轮复习-7.2-空间点、直线、平面之间的位置关系-专项训练【含解析】,共9页。
这是一份2025年高考数学一轮复习课时作业-空间点、直线、平面之间的位置关系【含解析】,共16页。









