2025高考数学一轮复习-9.2-用样本估计总体-专项训练（含解析）

这是一份2025高考数学一轮复习-9.2-用样本估计总体-专项训练（含解析），共18页。

A. 众数为2B. 平均数为2.5C. 方差为1.6D. 标准差为4
2. [2023·广东茂名联考]已知甲组数据为：5 ，12 ，16 ，21 ，25 ，37 ，乙组数据为：1 ，6 ，14 ，18 ，38 ，39 ，则甲、乙的平均数、极差及中位数相同的是( )
A. 极差B. 平均数C. 中位数D. 都不相同
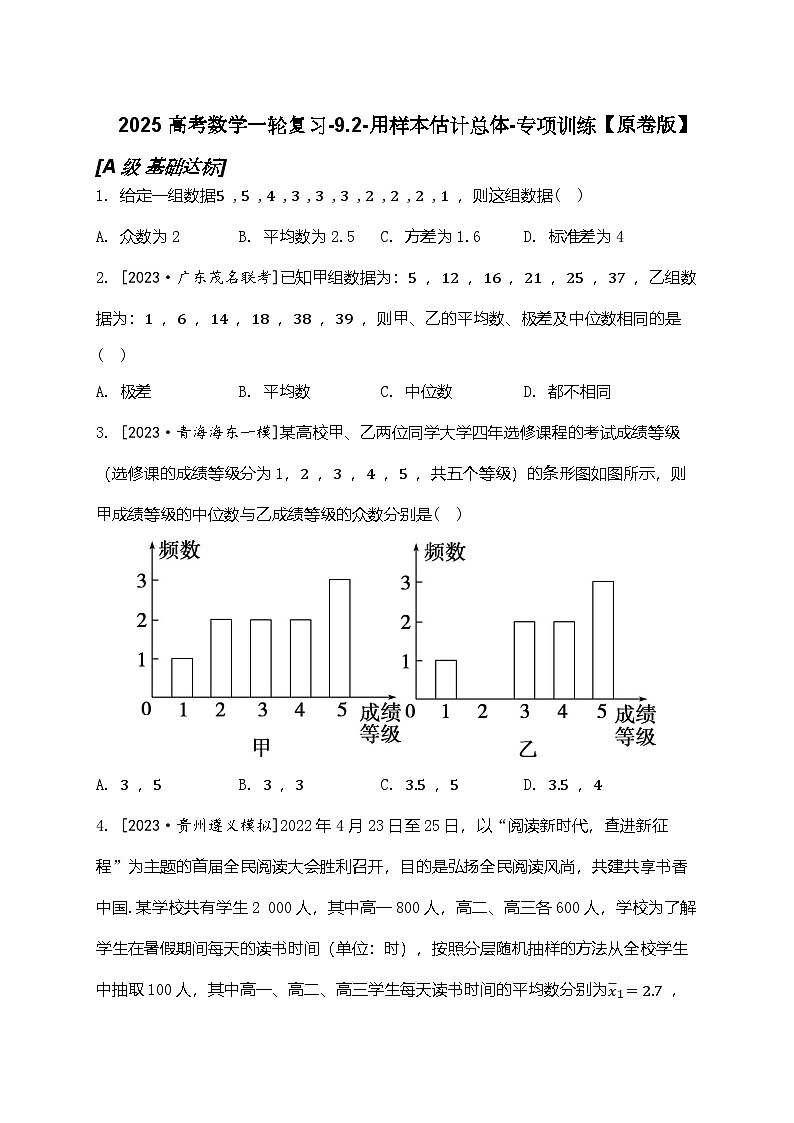
3. [2023·青海海东一模]某高校甲、乙两位同学大学四年选修课程的考试成绩等级（选修课的成绩等级分为1，2 ，3 ，4 ，5 ，共五个等级）的条形图如图所示，则甲成绩等级的中位数与乙成绩等级的众数分别是( )
A. 3 ，5 B. 3 ，3 C. 3.5 ，5 D. 3.5 ，4
4. [2023·贵州遵义模拟]2022年4月23日至25日，以“阅读新时代，查进新征程”为主题的首届全民阅读大会胜利召开，目的是弘扬全民阅读风尚，共建共享书香中国.某学校共有学生2 000人，其中高一800人，高二、高三各600人，学校为了解学生在暑假期间每天的读书时间（单位：时），按照分层随机抽样的方法从全校学生中抽取100人，其中高一、高二、高三学生每天读书时间的平均数分别为x1=2.7 ，x2=3.1 ，x3=3.3 ，每天读书时间的方差分别为s12=1 ,s22=2 ,s22=3 ,则下列说法错误的是( )
A. 从高一学生中抽取40人
B. 抽取的高二学生的总阅读时间是93时
C. 被抽取的学生每天的读书时间的平均数为2.8时
D. 估计全体学生每天的读书时间的方差为s2=1.966
5. （多选）下表为2022年某煤炭公司1~10月份的煤炭生产量：
则下列结论正确的是( )
A. 极差为12.5万吨B. 平均数为24万吨C. 中位数为24万吨D. 众数为17.5万吨
6. 从甲、乙、丙三个厂家生产的同一种产品中各抽取8件产品，对其使用寿命（单位：年）跟踪调查结果如下：
甲：3 ，4 ，5 ，6 ，8 ，8 ，8 ，10 ；
乙：4 ，6 ，6 ，6 ，8 ，9 ，12 ，13 ；
丙：3 ，3 ，4 ，7 ，9 ，10 ，11 ，12 .
三个厂家在广告中都称该产品的使用寿命是8年，请根据结果判断厂家在广告中分别运用了平均数、众数、中位数中的哪一种集中趋势的特征数：甲 ，乙 ，丙 .
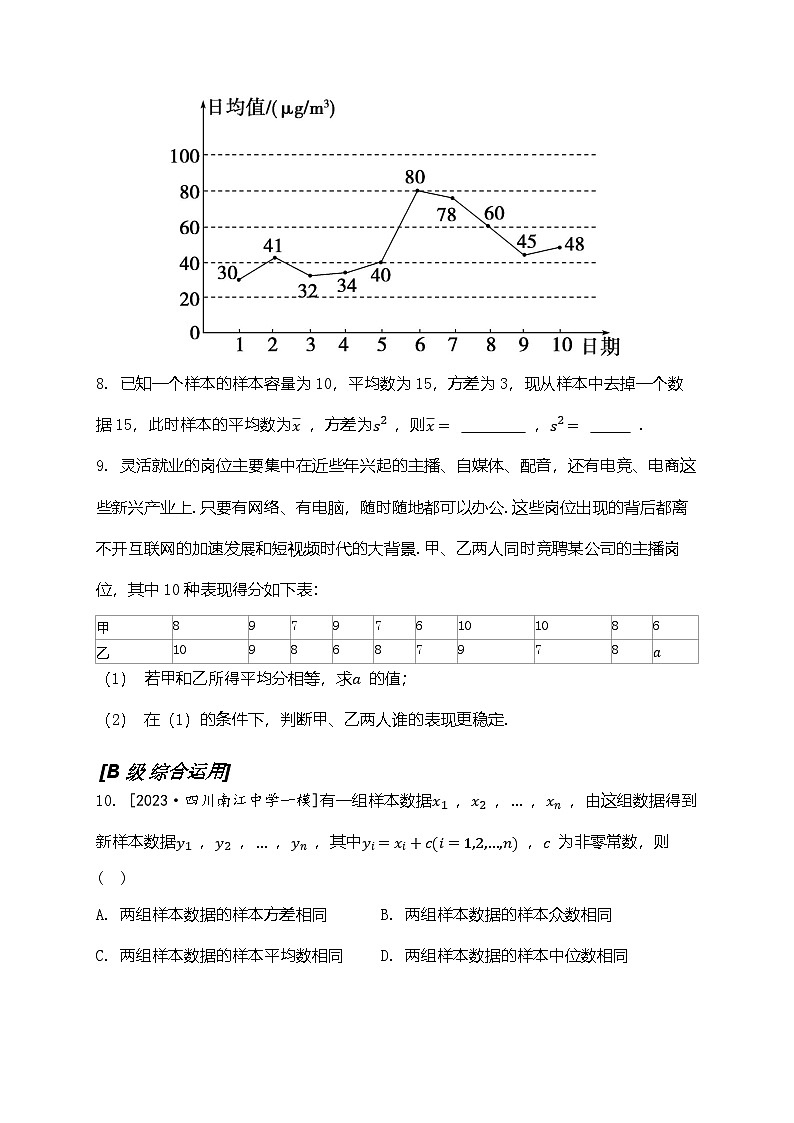
7. [2023·山东东营模拟]如图所示，某市5月1日至10日PM2.5 的日均值（单位：μg/m3 ）变化的折线图，则该组数据第64百分位数为 .
8. 已知一个样本的样本容量为10，平均数为15，方差为3，现从样本中去掉一个数据15，此时样本的平均数为x ，方差为s2 ，则x= ，s2= .
9. 灵活就业的岗位主要集中在近些年兴起的主播、自媒体、配音，还有电竞、电商这些新兴产业上.只要有网络、有电脑，随时随地都可以办公.这些岗位出现的背后都离不开互联网的加速发展和短视频时代的大背景.甲、乙两人同时竞聘某公司的主播岗位，其中10种表现得分如下表：
（1） 若甲和乙所得平均分相等，求a 的值；
（2） 在（1）的条件下，判断甲、乙两人谁的表现更稳定.
[B级 综合运用]
10. [2023·四川南江中学一模]有一组样本数据x1 ，x2 ，… ，xn ，由这组数据得到新样本数据y1 ，y2 ，… ，yn ，其中yi=xi+ci=1,2,…,n ，c 为非零常数，则( )
A. 两组样本数据的样本方差相同B. 两组样本数据的样本众数相同
C. 两组样本数据的样本平均数相同D. 两组样本数据的样本中位数相同
11. [2023·重庆第一学期考试]（多选）创新，是一个民族进步的灵魂，是一个国家兴旺发达的不竭源泉.为支持中小企业创新发展，国家决定对部分创新型企业的税收进行适当减免，现在全国调查了100家中小企业年收入情况，并根据所得数据画出了样本的频率分布直方图，则下列结论正确的是( )
A. 样本中年收入在[500,600) 的中小企业约有16家
B. 样本的中位数大于400万元
C. 估计全国中小企业年收入的平均数为376万元
D. 样本在区间[500,700] 内的频数为18
12. [2023·云南昆明模拟]为了解某种作物的生长情况，抽取该作物植株高度（单位：cm ）的一个随机样本，整理得到样本频率分布直方图如图所示.由此样本估计，该作物植株高度的80% 分位数约为 cm .
13. 某班成立了A ，B 两个数学兴趣小组，A 组10人，B 组30人，经过一周的补习后进行了一次测试，在该测试中，A 组的平均成绩为130分，方差为115，B 组的平均成绩为110分，方差为215.则在这次测试中全班学生的平均成绩和方差分别为 ， .
14. 某种治疗新冠感染的中药产品的质量以其质量指标值衡量，质量指标值越大表明质量越好.为了提高中药产品的质量，我国医疗科研专家攻坚克难，研发出A ，B 两种新配方，在这两种新配方生产的产品中随机抽取数量相同的样本，测量这些产品的质量指标值，规定质量指标值小于85为废品，在[85,115) 内为一等品，不小于115为特等品.现把测量数据整理如下，其中B 配方的样本中有6件废品.
A 配方的频率分布表
B 配方的频率分布直方图
（1） 求实数a ,b 的值；
（2） 试确定A 配方和B 配方哪一种更好.（说明：在统计方法中，同一组数据常用该组区间的中点值作代表）
[C级 素养提升]
15. （多选）某环保局对辖区内甲、乙、丙、丁四个地区的环境治理情况进行检查督导，若连续10天，每天空气质量指数（单位：μg/m3 ）不超过100，则认为该地区环境治理达标，否则认为该地区环境治理不达标.根据连续10天检查所得数据的数字特征推断，环境治理一定达标的地区是( )
A. 甲地区：平均数为80，方差为40B. 乙地区：平均数为50，众数为40
C. 丙地区：中位数为50，极差为60D. 丁地区：极差为10，80% 分位数为90
16. [2022·新高考卷Ⅱ]在某地区进行流行病学调查，随机调查了100位某种疾病患者的年龄，得到如下的样本数据的频率分布直方图：
（1） 估计该地区这种疾病患者的平均年龄（同一组中的数据用该组区间的中点值为代表）；
（2） 估计该地区一位这种疾病患者的年龄位于区间[20,70) 的概率；
（3） 已知该地区这种疾病的患病率为0.1% ，该地区年龄位于区间[40,50) 的人口占该地区总人口的16% .从该地区中任选一人，若此人的年龄位于区间[40,50) ，求此人患这种疾病的概率（以样本数据中患者的年龄位于各区间的频率作为患者的年龄位于该区间的概率，精确到0.000 1）.
2025高考数学一轮复习-9.2-用样本估计总体-专项训练【解析版】
[A级 基础达标]
1. 给定一组数据5 ,5 ,4 ,3 ,3 ,3 ,2 ,2 ,2 ,1 ，则这组数据( C )
A. 众数为2B. 平均数为2.5C. 方差为1.6D. 标准差为4
[解析]选C.由题中数据可得，众数为2和3，故A错误；平均数为x=5+5+…+2+110=3 ，故B错误；方差s2=5−32+5−32+…+2−32+1−3210=1.6 ,标准方差为1.6≠4 ,故C正确，D错误.
2. [2023·广东茂名联考]已知甲组数据为：5 ，12 ，16 ，21 ，25 ，37 ，乙组数据为：1 ，6 ，14 ，18 ，38 ，39 ，则甲、乙的平均数、极差及中位数相同的是( B )
A. 极差B. 平均数C. 中位数D. 都不相同
[解析]选B.由题中数据的分布，可知极差不同，甲的中位数为16+212=18.5 ，乙的中位数为14+182=16 ，x甲=5+12+16+21+25+376=583 ，x乙=1+6+14+18+38+396=583 ，所以甲、乙的平均数相同.
3. [2023·青海海东一模]某高校甲、乙两位同学大学四年选修课程的考试成绩等级（选修课的成绩等级分为1，2 ，3 ，4 ，5 ，共五个等级）的条形图如图所示，则甲成绩等级的中位数与乙成绩等级的众数分别是( C )
A. 3 ，5 B. 3 ，3 C. 3.5 ，5 D. 3.5 ，4
[解析]选C.由条形图可得，甲同学共有10门选修课，将这10门选修课的成绩等级从低到高排序后，第5，6 门的成绩等级分别为3，4 ，故中位数为3+42=3.5 ，乙成绩等级的众数为5.故选C.
4. [2023·贵州遵义模拟]2022年4月23日至25日，以“阅读新时代，查进新征程”为主题的首届全民阅读大会胜利召开，目的是弘扬全民阅读风尚，共建共享书香中国.某学校共有学生2 000人，其中高一800人，高二、高三各600人，学校为了解学生在暑假期间每天的读书时间（单位：时），按照分层随机抽样的方法从全校学生中抽取100人，其中高一、高二、高三学生每天读书时间的平均数分别为x1=2.7 ，x2=3.1 ，x3=3.3 ，每天读书时间的方差分别为s12=1 ,s22=2 ,s22=3 ,则下列说法错误的是( C )
A. 从高一学生中抽取40人
B. 抽取的高二学生的总阅读时间是93时
C. 被抽取的学生每天的读书时间的平均数为2.8时
D. 估计全体学生每天的读书时间的方差为s2=1.966
[解析]选C.对A，根据分层随机抽样，分别从高一、高二、高三学生中抽取40人、30人、30人，故A正确；对B，抽取的高二学生的总阅读时间是x2×30=93 （时）,故B正确；对C，被抽取的学生每天的读书时间的平均数为40100×2.7+30100×3.1+30100×3.3=3 （时），故C错误；对D，被抽取的学生每天的读书时间的方差为40100×[1+2.7−32]+30100×[2+3.1−32]+30100×[3+3.3−32]=1.966 ，所以估计全体学生每天的读书时间的方差为s2=1.966 ,故D正确.故选C.
5. （多选）下表为2022年某煤炭公司1~10月份的煤炭生产量：
则下列结论正确的是( ABD )
A. 极差为12.5万吨B. 平均数为24万吨C. 中位数为24万吨D. 众数为17.5万吨
[解析]选ABD.将表格中的数据由小到大排列依次为17.5，17.5 ，21 ，23 ，24 ，25 ，26 ，27 ，29 ，30 .极差为30−17.5=12.5 （万吨），A正确；平均数为17.5×2+21+23+24+25+26+27+29+3010=24 （万吨），B正确；中位数为25+242=24.5 （万吨），C错误；众数为17.5万吨，D正确.
6. 从甲、乙、丙三个厂家生产的同一种产品中各抽取8件产品，对其使用寿命（单位：年）跟踪调查结果如下：
甲：3 ，4 ，5 ，6 ，8 ，8 ，8 ，10 ；
乙：4 ，6 ，6 ，6 ，8 ，9 ，12 ，13 ；
丙：3 ，3 ，4 ，7 ，9 ，10 ，11 ，12 .
三个厂家在广告中都称该产品的使用寿命是8年，请根据结果判断厂家在广告中分别运用了平均数、众数、中位数中的哪一种集中趋势的特征数：甲众数，乙平均数，丙中位数.
[解析]甲、乙、丙三个厂家从不同角度描述了一组数据的特征，甲：该组数据8出现的次数最多；乙：该组数据的平均数x=4+6×3+8+9+12+138=8 ；丙：该组数据的中位数是7+92=8 .
7. [2023·山东东营模拟]如图所示，某市5月1日至10日PM2.5 的日均值（单位：μg/m3 ）变化的折线图，则该组数据第64百分位数为48.
[解析]该市5月1日至10日PM2.5 的日均值，从小到大依次为30,32 ,34 ,40 ,41 ,45 ，48 ，60 ，78 ，80 ,又10×0.64=6.4 ，所以第64百分位数为48.
8. 已知一个样本的样本容量为10，平均数为15，方差为3，现从样本中去掉一个数据15，此时样本的平均数为x ，方差为s2 ，则x= 15 ，s2= 103 .
[解析]设10个数据为x1 ,x2 ,… ,x9 ,15 ,
则x=15×10−159=15 .
又s2=x1−152+x2−152+…+x9−1529 ,x1−152+x2−152+⋯+x9−152+15−15210=3 ,
所以s2=309=103 .
9. 灵活就业的岗位主要集中在近些年兴起的主播、自媒体、配音，还有电竞、电商这些新兴产业上.只要有网络、有电脑，随时随地都可以办公.这些岗位出现的背后都离不开互联网的加速发展和短视频时代的大背景.甲、乙两人同时竞聘某公司的主播岗位，其中10种表现得分如下表：
（1） 若甲和乙所得平均分相等，求a 的值；
[答案]解：根据题中所给数据，x甲=110×8+9+7+9+7+6+10+10+8+6=8 ,
x ​乙=110×10+9+8+6+8+7+9+7+8+a=8 ,解得a=8 .
（2） 在（1）的条件下，判断甲、乙两人谁的表现更稳定.
[答案]s甲2=110×0+1+1+1+1+4+4+4+0+4=2 ,
s乙2=110×4+1+0+4+0+1+1+1+0+0=65 ，
由2>65 ,得乙的表现更稳定.
[B级 综合运用]
10. [2023·四川南江中学一模]有一组样本数据x1 ，x2 ，… ，xn ，由这组数据得到新样本数据y1 ，y2 ，… ，yn ，其中yi=xi+ci=1,2,…,n ，c 为非零常数，则( A )
A. 两组样本数据的样本方差相同B. 两组样本数据的样本众数相同
C. 两组样本数据的样本平均数相同D. 两组样本数据的样本中位数相同
[解析]选A.因为原来样本平均数x=1nx1+x2+…+xn ，新样本平均数y=1ny1+y2+…+yn=x+c ，C错误；原来样本方差为s12=1n[x1−x2+x2−x2+…+xn−x2] ，新样本方差为s22=1n[y1−y2+y2−y2+…+yn−y2]=s12 ，A正确；设原样本众数为a ，则新样本众数为a+c ，B错误；设原样本中位数为b ，则新样本中位数为b+c ，D错误.故选A.
11. [2023·重庆第一学期考试]（多选）创新，是一个民族进步的灵魂，是一个国家兴旺发达的不竭源泉.为支持中小企业创新发展，国家决定对部分创新型企业的税收进行适当减免，现在全国调查了100家中小企业年收入情况，并根据所得数据画出了样本的频率分布直方图，则下列结论正确的是( CD )
A. 样本中年收入在[500,600) 的中小企业约有16家
B. 样本的中位数大于400万元
C. 估计全国中小企业年收入的平均数为376万元
D. 样本在区间[500,700] 内的频数为18
[解析]选CD.由题图，得0.001+0.002+0.0026+0.0026+x+0.0004×100=1 ,解得x=0.0014 .
年收入在[500,600) 的中小企业约有0.0014×100×100=14 （家），故A不正确；
因为0.001+0.002×100=0.3<0.5 ,0.001+0.002+0.0026×100=0.56>0.5 ,
所以样本的中位数小于400万元，故B不正确；
由题图可知，样本中中小企业年收入的平均数为[0.001×150+0.002×250+0.0026×350+450+0.0014×550+0.0004×650]×100=376 （万元），所以估计全国中小企业年收入的平均数为376万元，故C正确；
样本在区间[500,700] 内的频数为0.0014+0.0004×100×100=18 ，故D正确.综上所述，选CD.
12. [2023·云南昆明模拟]为了解某种作物的生长情况，抽取该作物植株高度（单位：cm ）的一个随机样本，整理得到样本频率分布直方图如图所示.由此样本估计，该作物植株高度的80% 分位数约为78cm .
[解析]由题图可知，前三组从左到右矩形的面积为0.2 ，0.4 ，0.25 ，因为0.2+0.4+0.25=0.85>0.8 ，所以80% 分位数位于第3个矩形，设80% 分位数为x ，所以x=70+0.8−−0.6×10=78 .
13. 某班成立了A ，B 两个数学兴趣小组，A 组10人，B 组30人，经过一周的补习后进行了一次测试，在该测试中，A 组的平均成绩为130分，方差为115，B 组的平均成绩为110分，方差为215.则在这次测试中全班学生的平均成绩和方差分别为115，265.
[解析]依题意xA=130 ,sA2=115 ,xB=110 ,sB2=215 ,所以x=1010+30×130+3010+30×110=115 （分）,所以全班学生的平均成绩为115分.全班学生成绩的方差为s2=1010+30[sA2+xA−x2]+3010+30[sB2+xB−x2]=1010+30×115+225+3010+30×215+25=85+180=265 .
14. 某种治疗新冠感染的中药产品的质量以其质量指标值衡量，质量指标值越大表明质量越好.为了提高中药产品的质量，我国医疗科研专家攻坚克难，研发出A ，B 两种新配方，在这两种新配方生产的产品中随机抽取数量相同的样本，测量这些产品的质量指标值，规定质量指标值小于85为废品，在[85,115) 内为一等品，不小于115为特等品.现把测量数据整理如下，其中B 配方的样本中有6件废品.
A 配方的频率分布表
B 配方的频率分布直方图
（1） 求实数a ,b 的值；
[答案]解：依题意，A ，B 两种配方的样本容量相同，设为n .
由B 配方的样本中有6件废品，结合B 配方的频率分布直方图，得6n=0.006×10 ,解得n=100 .
所以a=100−8+36+24+8=24 .
由0.006+b+0.038+0.022+0.008×10=1 ,得b=0.026 .
所以实数a ,b 的值分别为24，0.026 .
（2） 试确定A 配方和B 配方哪一种更好.（说明：在统计方法中，同一组数据常用该组区间的中点值作代表）
[答案]由（1）及A 配方的频数分布表得，
A 配方质量指标值的样本平均数xA=80×8+90×24+100×36+110×24+120×8100=100 ，
A 配方质量指标值的样本方差sA2=1100×[−202×8+−102×24+0×36+102×24+202×8]=112 .
由（1）及B 配方的频率分布直方图得，
B 配方质量指标值的样本平均数xB=80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100 ，
B 配方质量指标值的样本方差sB2=−202×0.06+−102×0.26+0×0.38+102×0.22+202×0.08=104 .
综上，xA=xB ，sA2>sB2 ,
即A ，B 两种配方质量指标值的样本平均数相等，但A 配方质量指标值没有B 配方质量指标值稳定.
所以B 配方更好.
[C级 素养提升]
15. （多选）某环保局对辖区内甲、乙、丙、丁四个地区的环境治理情况进行检查督导，若连续10天，每天空气质量指数（单位：μg/m3 ）不超过100，则认为该地区环境治理达标，否则认为该地区环境治理不达标.根据连续10天检查所得数据的数字特征推断，环境治理一定达标的地区是( AD )
A. 甲地区：平均数为80，方差为40B. 乙地区：平均数为50，众数为40
C. 丙地区：中位数为50，极差为60D. 丁地区：极差为10，80% 分位数为90
[解析]选AD.设每天的空气质量指数为xii=1,2,…,10 ，则方差s2=110∑10i=1xi−x2 .
对于A，由110∑10i=1xi−802=40 ，得∑10i=1xi−802=400 ，如果这10天中有1天的空气质量指数超过100，则必有∑10i=1xi−802＞400 矛盾，所以这10天每天的空气质量指数都不超过100 ，A正确.对于B，如果有8天为40，有1天为150，有1天为30，此时平均数为50，众数为40，但该地区环境治理不达标，B错误.对于C，第1天为110，后面9天为50，此时中位数为50，极差为60，但该地区环境治理不达标，C错误.对于D，如果最大值超过100，根据极差为10，则最小值超过90，这与80％ 分位数为90矛盾，故最大值不超过100 ，D正确.故选AD.
16. [2022·新高考卷Ⅱ]在某地区进行流行病学调查，随机调查了100位某种疾病患者的年龄，得到如下的样本数据的频率分布直方图：
（1） 估计该地区这种疾病患者的平均年龄（同一组中的数据用该组区间的中点值为代表）；
[答案]解：估计该地区这种疾病患者的平均年龄x=10×5×0.001+15×0.002+25×0.012+35×0.017+45×0.023+55×0.020+65×0.017+75×0.006+85×0.002=47.9 .
（2） 估计该地区一位这种疾病患者的年龄位于区间[20,70) 的概率；
[答案]方法一：由于患者的年龄位于区间[20,70) 是由患者的年龄位于区间[20,30) ，[30,40) ，[40,50) ，[50,60) ，[60,70) 组成的，且相互独立，
所以所求概率P=0.012+0.017×2+0.023+0.020×10=0.89 .
方法二：由于患者的年龄位于区间[20,70) 是由患者的年龄位于区间[20,30) ，[30,40) ，[40,50) ，[50,60) ，[60,70) 组成的，且相互独立，所以所求概率P=1−0.001+0.002+0.006+0.002×10=0.89 .
（3） 已知该地区这种疾病的患病率为0.1% ，该地区年龄位于区间[40,50) 的人口占该地区总人口的16% .从该地区中任选一人，若此人的年龄位于区间[40,50) ，求此人患这种疾病的概率（以样本数据中患者的年龄位于各区间的频率作为患者的年龄位于该区间的概率，精确到0.000 1）.
[答案]设从该地区任选一人，年龄位于区间[40,50) 为事件A ，患这种疾病为事件B ，则PA=16% ，
由频率分布直方图知这种疾病患者年龄位于区间[40,50) 的概率为0.023×10=0.23 ,
结合该地区这种疾病的患病率为0.1% ，可得PAB=0.1%×0.23=0.00023 ，
所以从该地区任选一人，若年龄位于区间[40,50) ，则此人患这种疾病的概率为PB|A=PABPA=0.0002316%≈0.0014 .
月份
1
2
3
4
5
6
7
8
9
10
产量（单位：万吨）
23
25
24
17.5
17.5
21
26
29
30
27
甲
8
9
7
9
7
6
10
10
8
6
乙
10
9
8
6
8
7
9
7
8
a
质量指标值
[75,85)
[85,95)
[95,105)
[105,115)
[115,125]
频数
8
a
36
24
8
月份
1
2
3
4
5
6
7
8
9
10
产量（单位：万吨）
23
25
24
17.5
17.5
21
26
29
30
27
甲
8
9
7
9
7
6
10
10
8
6
乙
10
9
8
6
8
7
9
7
8
a
质量指标值
[75,85)
[85,95)
[95,105)
[105,115)
[115,125]
频数
8
a
36
24
8