2025高考数学一轮复习-第34讲-直线、平面平行的判定与性质-专项训练【含答案】

这是一份2025高考数学一轮复习-第34讲-直线、平面平行的判定与性质-专项训练【含答案】，共5页。
基 础 巩固练
1.已知平面α∥平面β,直线a∥平面α,直线b∥平面β,那么a与b的位置关系可能是( )

A.平行或相交B.相交或异面
C.平行或异面D.平行、相交或异面
2.若平面α∥平面β,点A,C∈α,B,D∈β,则直线AC∥直线BD的充要条件是( )
A.AB∥CD
B.AD∥CB
C.AB与CD相交
D.A,B,C,D四点共面
3.若平面β截三棱锥所得的截面为平行四边形,则该三棱锥的所有棱中与平面β平行的棱有( )
A.0条B.1条
C.2条D.1条或2条
4.(2023泰州月考)如图,在三棱柱ABC-A1B1C1中,AM=2MA1,BN=2NB1,过MN作一平面交底面三角形ABC的边BC,AC分别于点E,F,则( )
A.MF∥NE
B.四边形MNEF为梯形
C.四边形MNEF为平行四边形
D.A1B1∥NE
5.(多选题)(2023镇江调研)m,n是不同的直线,α,β是不同的平面,下列命题中的假命题为( )
A.若m⊂α,n∥α,则m∥n
B.若m∥α,m∥β,则α∥β
C.若α∥β,m⊂β,则m∥α
D.若α∥β,m∥α,则m∥β
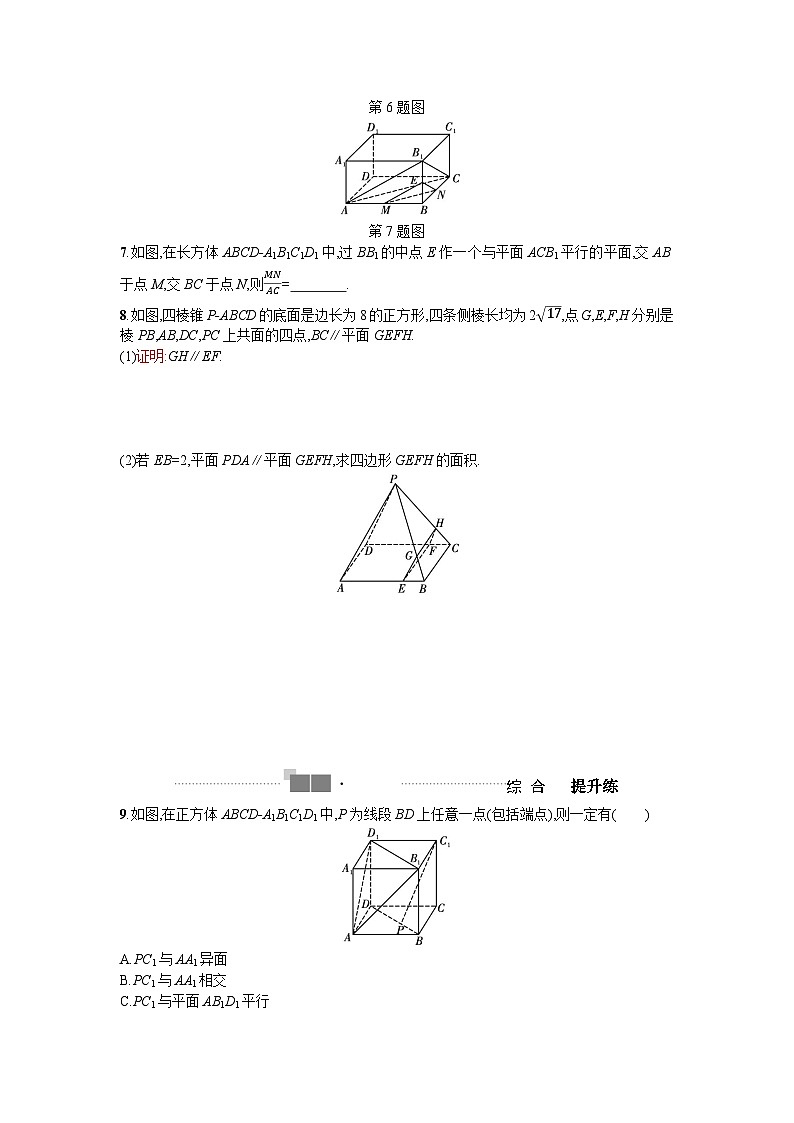
6.(2023南京调研)如图,P为平行四边形ABCD所在平面外一点,E为AD上一点,且AEED=13,F为PC上一点,当PA∥平面EBF时,PFFC= .
第6题图
第7题图
7.如图,在长方体ABCD-A1B1C1D1中,过BB1的中点E作一个与平面ACB1平行的平面,交AB于点M,交BC于点N,则MNAC= .
8.如图,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为217,点G,E,F,H分别是棱PB,AB,DC,PC上共面的四点,BC∥平面GEFH.
(1)证明:GH∥EF.
(2)若EB=2,平面PDA∥平面GEFH,求四边形GEFH的面积.
综 合 提升练
9.如图,在正方体ABCD-A1B1C1D1中,P为线段BD上任意一点(包括端点),则一定有( )
A.PC1与AA1异面
B.PC1与AA1相交
C.PC1与平面AB1D1平行
D.PC1与平面AB1D1相交
10.(2023连云港期中)如图,在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是A1D1,A1B1的中点,过直线BD的平面α与平面AMN平行,则平面α截该正方体所得截面的面积为( )
A.2B.98C.3D.62
11.有一木块如图所示,点P在平面A'B'C'D'内,棱BC∥平面A'B'C'D',要经过P和棱BC将木块锯开,锯开的面必须平整,有N种锯法,N=( )
A.0B.1C.2D.3
12.(2023无锡调研)设α∥β,A∈α,B∈β,C是AB的中点,当A,B分别在平面α,β内运动时,那么所有的动点C( )
A.不共面
B.当且仅当A,B分别在两条直线上移动时才共面
C.当且仅当A,B分别在两条给定的异面直线上移动时才共面
D.不论A,B如何移动,都共面
13.在长方体ABCD-A1B1C1D1中,DA=DC=1,DD1=2,分别在对角线A1D,CD1上取点M,N,使得直线MN∥平面A1ACC1,则线段MN长的最小值为 .
14.(2023南京质检)如图所示,正方体ABCD-A1B1C1D1的棱长为a,点P是棱AD上一点,且AP=a3,过点B1,D1,P的平面与底面ABCD的交线为PQ,点Q在直线CD上,则PQ= .
15.(2023淮安调研)如图,在等腰直角三角形PAD中,∠A=90°,AD=8,AB=3,B,C分别是PA,PD上的点,且AD∥BC,M,N分别为BP,CD的中点,现将△BCP沿BC折起,得到四棱锥P-ABCD,连接MN.证明:MN∥平面PAD.
创 新 应用练
16.如图,在棱长为1的正方体ABCD-A1B1C1D1中,P为棱BB1的中点,Q为正方形BB1C1C内一动点(含边界),若D1Q∥平面A1PD,则线段D1Q长度的取值范围为 .
参考答案
1.D 2.D 3.C 4.B 5.ABD
6.14 7.12
8.解 (1)∵BC∥平面GEFH,
BC⊂平面PBC,且平面PBC∩平面GEFH=GH,
∴BC∥GH.
又BC∥平面GEFH,BC⊂平面ABCD,且平面ABCD∩平面GEFH=EF,
∴BC∥EF,
∴EF∥GH.
(2)∵平面PDA∥平面GEFH,
平面PAB∩平面PAD=PA,且平面PAB∩平面GEFH=GE,
∴GE∥PA,∵BE=2,BA=8,
∴BE=14BA,∴GE=14PA=172,
同理可得HF=14PD=172,
又由(1)知,BC∥GH,∴GH=34BC=6,
在四边形GEFH中,GE=HF=172,GH=6,EF=8且EF∥GH,
∴四边形GEFH为等腰梯形,
如图,过点G作GM⊥EF于点M,
过点H作HN⊥EF于点N,
在Rt△GEM中,GM=GE2-EM2=132,
∴S梯形EFGH=12(GH+EF)·GM=7132.
9.C 10.B 11.B 12.D 13.23
14.223a
15.解 如图,在四棱锥P-ABCD中,取AB的中点E,连接EM,EN.
因为M,N分别为BP,CD的中点,AD∥BC,
所以ME∥PA,EN∥AD,
又PA⊂平面PAD,ME⊄平面PAD,
所以ME∥平面PAD,
同理可得,EN∥平面PAD,
又ME∩EN=E,ME,EN⊂平面MNE,
所以平面MNE∥平面PAD,
因为MN⊂平面MNE,
所以MN∥平面PAD.
16.324,52