新高考数学一轮复习分层提升练习第36练 空间向量及其应用（2份打包，原卷版+含解析）

这是一份新高考数学一轮复习分层提升练习第36练 空间向量及其应用（2份打包，原卷版+含解析），文件包含新高考数学一轮复习分层提升练习第36练空间向量及其应用原卷版doc、新高考数学一轮复习分层提升练习第36练空间向量及其应用含解析doc等2份试卷配套教学资源，其中试卷共145页， 欢迎下载使用。
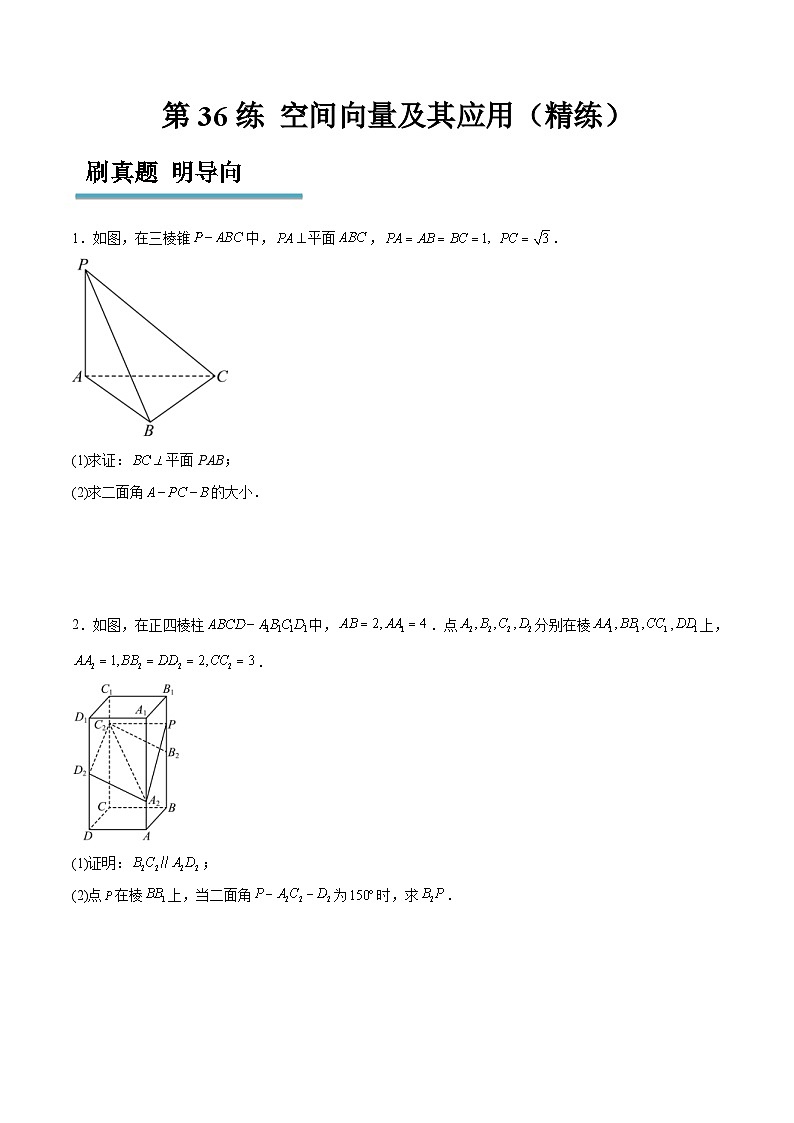
1．如图，在三棱锥 SKIPIF 1 < 0 中， SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．

(1)求证： SKIPIF 1 < 0 平面PAB；
(2)求二面角 SKIPIF 1 < 0 的大小．
2．如图，在正四棱柱 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ．点 SKIPIF 1 < 0 分别在棱 SKIPIF 1 < 0 , SKIPIF 1 < 0 上， SKIPIF 1 < 0 ．

(1)证明： SKIPIF 1 < 0 ；
(2)点 SKIPIF 1 < 0 在棱 SKIPIF 1 < 0 上，当二面角 SKIPIF 1 < 0 为 SKIPIF 1 < 0 时，求 SKIPIF 1 < 0 ．
3．如图，三棱锥 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，E为BC的中点．

(1)证明： SKIPIF 1 < 0 ；
(2)点F满足 SKIPIF 1 < 0 ，求二面角 SKIPIF 1 < 0 的正弦值．
4．直三棱柱 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，D为 SKIPIF 1 < 0 的中点，E为 SKIPIF 1 < 0 的中点，F为 SKIPIF 1 < 0 的中点．
(1)求证： SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)求直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的正弦值；
(3)求平面 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 夹角的余弦值．
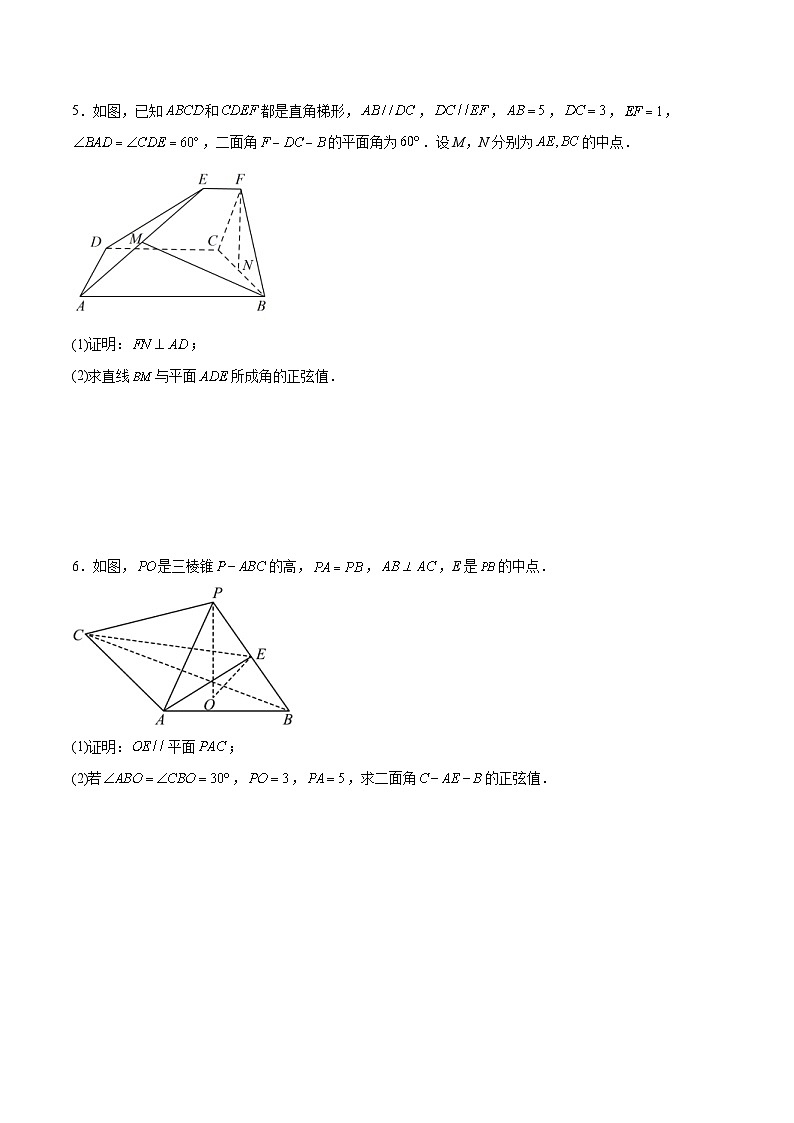
5．如图，已知 SKIPIF 1 < 0 和 SKIPIF 1 < 0 都是直角梯形， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，二面角 SKIPIF 1 < 0 的平面角为 SKIPIF 1 < 0 ．设M，N分别为 SKIPIF 1 < 0 的中点．
(1)证明： SKIPIF 1 < 0 ；
(2)求直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的正弦值．
6．如图， SKIPIF 1 < 0 是三棱锥 SKIPIF 1 < 0 的高， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，E是 SKIPIF 1 < 0 的中点．

(1)证明： SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求二面角 SKIPIF 1 < 0 的正弦值．
7．在四棱锥 SKIPIF 1 < 0 中， SKIPIF 1 < 0 底面 SKIPIF 1 < 0 ．
(1)证明： SKIPIF 1 < 0 ；
(2)求PD与平面 SKIPIF 1 < 0 所成的角的正弦值．
8．如图，四面体 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，E为 SKIPIF 1 < 0 的中点．
(1)证明：平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)设 SKIPIF 1 < 0 ，点F在 SKIPIF 1 < 0 上，当 SKIPIF 1 < 0 的面积最小时，求 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成的角的正弦值．
9．如图，在三棱柱 SKIPIF 1 < 0 中，侧面 SKIPIF 1 < 0 为正方形，平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，M，N分别为 SKIPIF 1 < 0 ，AC的中点．
(1)求证： SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)再从条件①、条件②这两个条件中选择一个作为已知，求直线AB与平面BMN所成角的正弦值．
条件①： SKIPIF 1 < 0 ；
条件②： SKIPIF 1 < 0 ．
注：如果选择条件①和条件②分别解答，按第一个解答计分．
10．如图，直三棱柱 SKIPIF 1 < 0 的体积为4， SKIPIF 1 < 0 的面积为 SKIPIF 1 < 0 ．
(1)求A到平面 SKIPIF 1 < 0 的距离；
(2)设D为 SKIPIF 1 < 0 的中点， SKIPIF 1 < 0 ，平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ，求二面角 SKIPIF 1 < 0 的正弦值．
【A组】
1．如图，在三棱柱 SKIPIF 1 < 0 中， SKIPIF 1 < 0 平面 SKIPIF 1 < 0 为线段 SKIPIF 1 < 0 的中点．
(1)求证： SKIPIF 1 < 0 ；
(2)求直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角大小．
2．已知四棱锥P-ABCD中，PD⊥平面ABCD， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，AB⊥DA，AB∥CD．
(1)求证：平面PAD⊥平面PCD；
(2)设M是棱PC上的点，若二面角M-BD-A的余弦值为 SKIPIF 1 < 0 ，试求直线BC与平面BDM所成角的正弦值．
3．如图，在棱长为1的正方体 SKIPIF 1 < 0 中，E为线段 SKIPIF 1 < 0 的中点，F为线段 SKIPIF 1 < 0 的中点．
（1）求点 SKIPIF 1 < 0 到直线 SKIPIF 1 < 0 的距离；
（2）求点 SKIPIF 1 < 0 到平面 SKIPIF 1 < 0 的距离；
4．）如图，在三棱柱 SKIPIF 1 < 0 中，侧面 SKIPIF 1 < 0 为正方形，平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，M，N分别为 SKIPIF 1 < 0 ，AC的中点．
(1)求证： SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)若 SKIPIF 1 < 0 ，求直线AB与平面BMN所成角的正弦值．
5．如图，已知长方体 SKIPIF 1 < 0 ＝ SKIPIF 1 < 0 ＝1，直线BD与平面 SKIPIF 1 < 0 所成的角为30°，AE垂直BD于E，F为 SKIPIF 1 < 0 的中点．
(1)求异面直线AE与BF所成的角的余弦；
(2)求点A到平面BDF的距离．
6．在图1中，四边形 SKIPIF 1 < 0 为梯形， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，过点A作 SKIPIF 1 < 0 ，交 SKIPIF 1 < 0 于 SKIPIF 1 < 0 ．现沿 SKIPIF 1 < 0 将 SKIPIF 1 < 0 折起，使得 SKIPIF 1 < 0 ，得到如图2所示的四棱锥 SKIPIF 1 < 0 ，在图2中解答下列两问：
(1)求四棱锥 SKIPIF 1 < 0 的体积；
(2)若F在侧棱 SKIPIF 1 < 0 上， SKIPIF 1 < 0 ，求证：二面角 SKIPIF 1 < 0 为直二面角．
7．在斜三棱柱 SKIPIF 1 < 0 中， SKIPIF 1 < 0 是等腰直角三角形， SKIPIF 1 < 0 ，平面 SKIPIF 1 < 0 底面 SKIPIF 1 < 0 ， SKIPIF 1 < 0 .
(1)证明： SKIPIF 1 < 0 ；
(2)求二面角 SKIPIF 1 < 0 的正弦值.
8．如图所示，四棱锥 SKIPIF 1 < 0 的底面 SKIPIF 1 < 0 是矩形， SKIPIF 1 < 0 底面 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
(1)证明： SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)求直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的正弦值．
9．如图，在四棱锥 SKIPIF 1 < 0 中，底面四边形 SKIPIF 1 < 0 为菱形，点 SKIPIF 1 < 0 为棱 SKIPIF 1 < 0 的中点， SKIPIF 1 < 0 为边 SKIPIF 1 < 0 的中点.
(1)求证： SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)若侧面 SKIPIF 1 < 0 底面 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求平面 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 的夹角的余弦值.
10．如图，在三棱柱 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ．
(1)求证： SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)若 SKIPIF 1 < 0 ，Q是 SKIPIF 1 < 0 的重心，直线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 所成角的余弦值为 SKIPIF 1 < 0 ，求直线 SKIPIF 1 < 0 和平面 SKIPIF 1 < 0 所成角的正弦值．
11．在三棱锥 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的中点， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 的中点， SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ， SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成的角为 SKIPIF 1 < 0 ．
(1)求证： SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)求平面 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 的夹角的余弦值．
12．如图，在四棱锥 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，底面ABCD为菱形，边长为2， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，异面直线PB与CD所成的角为 SKIPIF 1 < 0 .

(1)求证: SKIPIF 1 < 0 平面ABCD;
(2)若E是线段OC的中点，求点E到直线BP的距离.
13．如图，在直三棱柱 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 分别是 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的中点，已知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
(1)证明： SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)求 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的正弦值；
(3)求 SKIPIF 1 < 0 到平面 SKIPIF 1 < 0 的距离．
14．如图，在四棱锥 SKIPIF 1 < 0 中， SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ，底面 SKIPIF 1 < 0 是直角梯形，其中 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，E为棱 SKIPIF 1 < 0 上的点，且 SKIPIF 1 < 0 .
(1)求证： SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)求二面角 SKIPIF 1 < 0 的余弦值；
(3)求点E到平面 SKIPIF 1 < 0 的距离.
15．图1是由矩形 SKIPIF 1 < 0 ， SKIPIF 1 < 0 和菱形 SKIPIF 1 < 0 组成的一个平面图形，其中 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．将该图形沿 SKIPIF 1 < 0 ， SKIPIF 1 < 0 折起使得 SKIPIF 1 < 0 与 SKIPIF 1 < 0 重合，连接 SKIPIF 1 < 0 ，如图2．
(1)证明：图2中C，D，E，G四点共面；
(2)求图2中二面角 SKIPIF 1 < 0 的平面角的余弦值．
16．某校积极开展社团活动，在一次社团活动过程中，一个数学兴趣小组发现《九章算术》中提到了“刍甍”这个五面体，于是他们仿照该模型设计了一道数学探究题，如图1，E、F、G分别是正方形的三边AB、CD、AD的中点，先沿着虚线段FG将等腰直角三角形FDG裁掉，再将剩下的五边形ABCFG沿着线段EF折起，连接AB、CG就得到了一个“刍甍”（如图2）．
(1)若 SKIPIF 1 < 0 是四边形 SKIPIF 1 < 0 对角线的交点，求证： SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)若正方形的变成为2，且二面角 SKIPIF 1 < 0 是直二面角，求点 SKIPIF 1 < 0 到平面 SKIPIF 1 < 0 的距离．
17．如图，在四棱锥 SKIPIF 1 < 0 中，平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 在棱 SKIPIF 1 < 0 上，设 SKIPIF 1 < 0 .
(1)证明： SKIPIF 1 < 0 .
(2)设二面角 SKIPIF 1 < 0 的平面角为 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的值.
18．在如图所示的圆柱 SKIPIF 1 < 0 中, SKIPIF 1 < 0 为圆 SKIPIF 1 < 0 的直径, SKIPIF 1 < 0 是 SKIPIF 1 < 0 上的两个三等分点, SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 都是圆柱 SKIPIF 1 < 0 的母线.
(1)求证： SKIPIF 1 < 0 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ;
(2)若 SKIPIF 1 < 0 已知直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角为 SKIPIF 1 < 0 求二面角 SKIPIF 1 < 0 的余弦值.
19．如图，三棱柱 SKIPIF 1 < 0 ，底面 SKIPIF 1 < 0 是边长为2的正三角形， SKIPIF 1 < 0 ，平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 .
(1)证明： SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)若 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的正弦值为 SKIPIF 1 < 0 ，求平面 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 夹角的余弦值.
20．如图,在四棱锥 SKIPIF 1 < 0 中, SKIPIF 1 < 0 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,正方形 SKIPIF 1 < 0 的对角线交于点O．
(1)求证: SKIPIF 1 < 0 SKIPIF 1 < 0 平面PAC;
(2)求二面角 SKIPIF 1 < 0 的余弦值．
21．如图，四边形 SKIPIF 1 < 0 为正方形，E，F分别为 SKIPIF 1 < 0 的中点，以 SKIPIF 1 < 0 为折痕把 SKIPIF 1 < 0 折起，使点C到达点P的位置，且平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ．
(1)证明： SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)求二面角 SKIPIF 1 < 0 的正弦值．
22．在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 分别 SKIPIF 1 < 0 上的点且 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，将 SKIPIF 1 < 0 沿 SKIPIF 1 < 0 折起到 SKIPIF 1 < 0 的位置，使 SKIPIF 1 < 0 ．
(1)求证： SKIPIF 1 < 0 ；
(2)是否在射线 SKIPIF 1 < 0 上存在点 SKIPIF 1 < 0 ，使平面 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的余弦值为 SKIPIF 1 < 0 ？若存在，求出 SKIPIF 1 < 0 的长度；若不存在，请说明理由．
【B组 】
1．如图，四棱锥 SKIPIF 1 < 0 的底面为正方形， SKIPIF 1 < 0 ， SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ， SKIPIF 1 < 0 分别是线段 SKIPIF 1 < 0 的中点， SKIPIF 1 < 0 是线段 SKIPIF 1 < 0 上的一点.

(1)求证：平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)若直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的正弦值为 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 点不是线段 SKIPIF 1 < 0 的中点，求三棱锥 SKIPIF 1 < 0 体积.
2．如图所示，直三棱柱 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 .

(1)求证： SKIPIF 1 < 0 ；
(2)求直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的正弦值.
3．在四棱锥 SKIPIF 1 < 0 中，底面ABCD为正方形，平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 .

(1)证明：平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)若E为PC的中点，异面直线BE与PA所成角为 SKIPIF 1 < 0 ，求四棱锥 SKIPIF 1 < 0 的体积.
4．如图， 在四棱锥 SKIPIF 1 < 0 中， SKIPIF 1 < 0 平面ABCD， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 . E为棱 PC上一点，平面ABE与棱PD交于点F. 且 SKIPIF 1 < 0 .

(1)求证: F为PD的中点；
(2)求二面角 SKIPIF 1 < 0 的余弦值.
5．如图，在三棱锥 SKIPIF 1 < 0 中， SKIPIF 1 < 0 底面 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 分别为棱 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 的中点， SKIPIF 1 < 0 是线段 SKIPIF 1 < 0 的中点， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
(1)求证： SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)求点 SKIPIF 1 < 0 到直线 SKIPIF 1 < 0 的距离；
(3)在线段 SKIPIF 1 < 0 上是否存在一点 SKIPIF 1 < 0 ，使得直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的正弦值为 SKIPIF 1 < 0 ，若存在，求出线段 SKIPIF 1 < 0 的值，若不存在，说明理由．
6．如图所示，在三棱锥 SKIPIF 1 < 0 中，已知 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ，平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ．

(1)证明： SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，在线段 SKIPIF 1 < 0 上（不含端点），是否存在点 SKIPIF 1 < 0 ，使得二面角 SKIPIF 1 < 0 的余弦值为 SKIPIF 1 < 0 ，若存在，确定点 SKIPIF 1 < 0 的位置；若不存在，说明理由．
7．如图，扇形 SKIPIF 1 < 0 的半径为 SKIPIF 1 < 0 ，圆心角 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 为 SKIPIF 1 < 0 上一点， SKIPIF 1 < 0 平面 SKIPIF 1 < 0 且 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 且 SKIPIF 1 < 0 ， SKIPIF 1 < 0 面 SKIPIF 1 < 0 ．

(1)求证： SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)求平面 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成二面角的正弦值的大小．
8．如图，在底面为正方形的四棱台 SKIPIF 1 < 0 中，已知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，A到平面 SKIPIF 1 < 0 的距离为 SKIPIF 1 < 0 .

(1)求 SKIPIF 1 < 0 到平面 SKIPIF 1 < 0 的距离；
(2)若 SKIPIF 1 < 0 ，求直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的正弦值.
9．已知四棱锥 SKIPIF 1 < 0 ，底面为菱形 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ， SKIPIF 1 < 0 为 SKIPIF 1 < 0 上一点.
(1)平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ，证明： SKIPIF 1 < 0 ；
(2)当二面角 SKIPIF 1 < 0 的余弦值为 SKIPIF 1 < 0 时，试确定点 SKIPIF 1 < 0 的位置.
10．如图，在四棱锥 SKIPIF 1 < 0 中， SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ，底面 SKIPIF 1 < 0 是矩形， SKIPIF 1 < 0 是 SKIPIF 1 < 0 上一点， SKIPIF 1 < 0 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 .

(1)求证： SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)从下面三个条件中任选一个补充在下面的横线上，并作答：①异面直线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 所成角的正切值为 SKIPIF 1 < 0 ；②直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的正弦值为 SKIPIF 1 < 0 ；③点 SKIPIF 1 < 0 到平面 SKIPIF 1 < 0 的距离为 SKIPIF 1 < 0 ；
若___________，求平面 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 夹角的余弦值.
11．如图，在四棱锥 SKIPIF 1 < 0 中， SKIPIF 1 < 0 分别为 SKIPIF 1 < 0 的中点，连接 SKIPIF 1 < 0 .

(1)当 SKIPIF 1 < 0 为 SKIPIF 1 < 0 上不与点 SKIPIF 1 < 0 重合的一点时，证明： SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)已知 SKIPIF 1 < 0 分别为 SKIPIF 1 < 0 的中点， SKIPIF 1 < 0 是边长为 SKIPIF 1 < 0 的正三角形，四边形 SKIPIF 1 < 0 是面积为 SKIPIF 1 < 0 的矩形，当 SKIPIF 1 < 0 时，求 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的正弦值.
12．如图，在五棱锥 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 .

(1)证明： SKIPIF 1 < 0 ；
(2)若平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ，平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ，探索： SKIPIF 1 < 0 是否为定值？若为定值，请求出 SKIPIF 1 < 0 的值；若不是定值，请说明理由.
13．如图，在四棱锥 SKIPIF 1 < 0 中， SKIPIF 1 < 0 为直角梯形， SKIPIF 1 < 0 ，平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ． SKIPIF 1 < 0 是以 SKIPIF 1 < 0 为斜边的等腰直角三角形， SKIPIF 1 < 0 为 SKIPIF 1 < 0 上一点，且 SKIPIF 1 < 0 ．

(1)证明：直线 SKIPIF 1 < 0 ∥平面 SKIPIF 1 < 0 ;
(2)求二面角 SKIPIF 1 < 0 的余弦值．
14．如图，该几何体是由等高的半个圆柱和 SKIPIF 1 < 0 个圆柱拼接而成，点 SKIPIF 1 < 0 为弧 SKIPIF 1 < 0 的中点，且 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 四点共面.

(1)证明：平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)若平面 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成二面角的余弦值为 SKIPIF 1 < 0 ，且线段 SKIPIF 1 < 0 长度为2，求点 SKIPIF 1 < 0 到直线 SKIPIF 1 < 0 的距离.
15．如图，平行六面体 SKIPIF 1 < 0 的体积为6，截面 SKIPIF 1 < 0 的面积为6．

(1)求点 SKIPIF 1 < 0 到平面 SKIPIF 1 < 0 的距离；
(2)若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的正弦值．
16．如图，在三棱锥 SKIPIF 1 < 0 中， SKIPIF 1 < 0 平面ABD，E为AB的中点， SKIPIF 1 < 0 ， SKIPIF 1 < 0 .

(1)证明： SKIPIF 1 < 0 平面CED；
(2)当二面角 SKIPIF 1 < 0 的大小为30°，求 SKIPIF 1 < 0 与平面ACD所成角的正弦值.
17．如图，在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，E为AB中点，过点E作ED垂直AC于D，将 SKIPIF 1 < 0 沿ED翻折，使得面 SKIPIF 1 < 0 面 SKIPIF 1 < 0 ，点M是棱AC上一点，且 SKIPIF 1 < 0 面 SKIPIF 1 < 0 ．

(1)求 SKIPIF 1 < 0 的值；
(2)求二面角 SKIPIF 1 < 0 的余弦值．
18．如图1，在等腰梯形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，沿 SKIPIF 1 < 0 将 SKIPIF 1 < 0 折成 SKIPIF 1 < 0 ，如图2所示，连接 SKIPIF 1 < 0 ，得到四棱锥 SKIPIF 1 < 0 .
(1)若平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ，求证： SKIPIF 1 < 0 ；
(2)若点 SKIPIF 1 < 0 是 SKIPIF 1 < 0 的中点，求点 SKIPIF 1 < 0 到直线 SKIPIF 1 < 0 的距离的取值范围.
【C组】
1.如图，在四棱锥 SKIPIF 1 < 0 中，底面 SKIPIF 1 < 0 为直角梯形，其中 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 在棱 SKIPIF 1 < 0 上，点 SKIPIF 1 < 0 为 SKIPIF 1 < 0 中点.
(1)证明：若 SKIPIF 1 < 0 ，直线 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)求二面角 SKIPIF 1 < 0 的正弦值；
(3)是否存在点 SKIPIF 1 < 0 ，使 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的正弦值为 SKIPIF 1 < 0 ？若存在求出 SKIPIF 1 < 0 值；若不存在，说明理由.
2．如图，在四棱锥 SKIPIF 1 < 0 中，底面 SKIPIF 1 < 0 为直角梯形， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，E为 SKIPIF 1 < 0 的中点，且 SKIPIF 1 < 0 ．
(1)求证： SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)记 SKIPIF 1 < 0 的中点为N，若M在线段 SKIPIF 1 < 0 上，且直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的正弦值为 SKIPIF 1 < 0 ，求线段 SKIPIF 1 < 0 的长．
3．如图，在三棱锥D—ABC中，G是△ABC的重心，E，F分别在BC，CD上，且 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
(1)证明：平面 SKIPIF 1 < 0 平面ABD；
(2)若 SKIPIF 1 < 0 平面ABC， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，P是线段EF上一点，当线段GP长度取最小值时，求二面角 SKIPIF 1 < 0 的余弦值．
4．如图甲，等腰梯形ABCD中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 于点E，且 SKIPIF 1 < 0 ，将梯形沿着DE翻折，如图乙，使得A到Р点，且 SKIPIF 1 < 0 .
(1)求直线PD与平面EBCD所成角的正弦值；
(2)若 SKIPIF 1 < 0 ，求三棱锥 SKIPIF 1 < 0 的表面积.
5．如图，四棱锥P-ABCD中，侧面PAD为等边三角形且垂直于底面ABCD， SKIPIF 1 < 0 ，∠BAD=∠ABC=90°，E是PD的中点.
(1)证明：直线CE∥平面PAB；
(2)点M在棱PC上，且直线BM与底面ABCD所成角为45°，求二面角M-AB-D的余弦值.
6．如图1，已知等边 SKIPIF 1 < 0 的边长为 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 分别是边 SKIPIF 1 < 0 上的点，且满足 SKIPIF 1 < 0 ，如图2，将 SKIPIF 1 < 0 沿 SKIPIF 1 < 0 折起到 SKIPIF 1 < 0 的位置．
(1)求证：平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)给出三个条件：① SKIPIF 1 < 0 ；②平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；③四棱锥 SKIPIF 1 < 0 的体积为 SKIPIF 1 < 0 ，从中任选一个，求平面 SKIPIF 1 < 0 和平面 SKIPIF 1 < 0 的夹角的余弦值．
7．如图，在以P，A，B，C，D为顶点的五面体中，四边形ABCD为等腰梯形， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
(1)求证：平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)若二面角 SKIPIF 1 < 0 的余弦值为 SKIPIF 1 < 0 ，求直线PD与平面PBC所成角的大小．
8．如图，圆台下底面圆 SKIPIF 1 < 0 的直径为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 是圆 SKIPIF 1 < 0 上异于 SKIPIF 1 < 0 的点，且 SKIPIF 1 < 0 ， SKIPIF 1 < 0 为上底面圆 SKIPIF 1 < 0 的一条直径， SKIPIF 1 < 0 是边长为 SKIPIF 1 < 0 的等边三角形， SKIPIF 1 < 0 .
(1)证明： SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)求平面 SKIPIF 1 < 0 和平面 SKIPIF 1 < 0 夹角的余弦值.
9．如图，在三棱台ABC－A1B1C1中，底面△ABC是等腰三角形，且BC＝8，AB＝AC＝5，O为BC的中点．侧面BCC1B1为等腰梯形，且B1C1＝CC1＝4，M为B1C1中点．
(1)证明：平面ABC⊥平面AOM；
(2)记二面角A－BC－B1的大小为θ，当θ∈[ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ]时，求直线BB1平面AA1C1C所成角的正弦的最大值．
10．如图，C是以 SKIPIF 1 < 0 为直径的圆O上异于A，B的点，平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 为正三角形，E，F分别是 SKIPIF 1 < 0 上的动点.
(1)求证： SKIPIF 1 < 0 ；
(2)若E，F分别是 SKIPIF 1 < 0 的中点且异面直线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 所成角的正切值为 SKIPIF 1 < 0 ，记平面 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 的交线为直线l，点Q为直线l上动点，求直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的取值范围.