2023-2024学年陕西省咸阳市永寿县上邑乡部分学校七年级（下）期末数学试卷（含答案）

这是一份2023-2024学年陕西省咸阳市永寿县上邑乡部分学校七年级（下）期末数学试卷（含答案），共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.蚕丝是大自然中的天然纤维，柔韧绵长.某蚕丝的直径大约是0.000014米，0.000014用科学记数法表示为( )
A. 0.14×10−4B. 1.4×10−4C. 1.4×10−5D. 14×10−4
2.如图所示图形中，不是轴对称图形的是( )
A. B. C. D.
3.如图，△ABC是直角三角形，∠ABC=90°，MN//PQ.若∠MDB=110°，则∠CBQ的度数是( )
A. 20°B. 30°C. 35°D. 40°
4.下列运算正确的是( )
A. (a+b)2=a2+b2B. (−a3)⋅a=a4
C. (a2b3)2=a4b6D. (−m)6÷(−m)2=−m4
5.在学习了“用频率估计概率”这一节内容后，某课外兴趣小组利用计算器进行模拟试验来探究“6个人中有2个人同月过生日的概率”，他们将试验中获得的数据记录如下：
通过试验，该小组估计“6个人中有2个人同月过生日”的概率(精确到0.01)大约是( )
A. 0.8B. 0.784C. 0.78D. 0.76
6.如图，在大烧杯中放了一个小烧杯，现向小烧杯中匀速注水，小烧杯满了后继续匀速注水，则大烧杯的液面高度ℎ(cm)与时间注水时间t(s)的大致图象是( )
A. B. C. D.
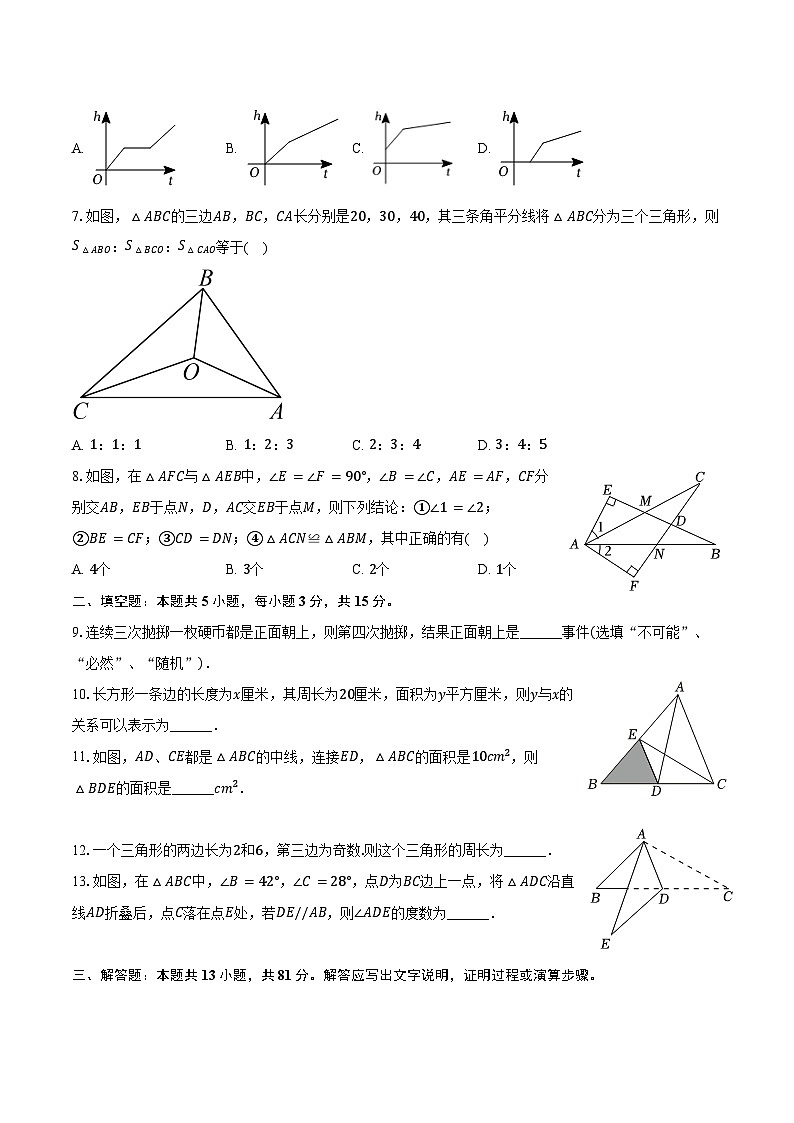
7.如图，△ABC的三边AB，BC，CA长分别是20，30，40，其三条角平分线将△ABC分为三个三角形，则S△ABO：S△BCO：S△CAO等于( )
A. 1：1：1B. 1：2：3C. 2：3：4D. 3：4：5
8.如图，在△AFC与△AEB中，∠E=∠F=90°，∠B=∠C，AE=AF，CF分别交AB，EB于点N，D，AC交EB于点M，则下列结论：①∠1=∠2；②BE=CF；③CD=DN；④△ACN≌△ABM，其中正确的有( )
A. 4个B. 3个C. 2个D. 1个
二、填空题：本题共5小题，每小题3分，共15分。
9.连续三次抛掷一枚硬币都是正面朝上，则第四次抛掷，结果正面朝上是______事件(选填“不可能”、“必然”、“随机”)．
10.长方形一条边的长度为x厘米，其周长为20厘米，面积为y平方厘米，则y与x的关系可以表示为______．
11.如图，AD、CE都是△ABC的中线，连接ED，△ABC的面积是10cm2，则△BDE的面积是______cm2．
12.一个三角形的两边长为2和6，第三边为奇数.则这个三角形的周长为______．
13.如图，在△ABC中，∠B=42°，∠C=28°，点D为BC边上一点，将△ADC沿直线AD折叠后，点C落在点E处，若DE//AB，则∠ADE的度数为______．
三、解答题：本题共13小题，共81分。解答应写出文字说明，证明过程或演算步骤。
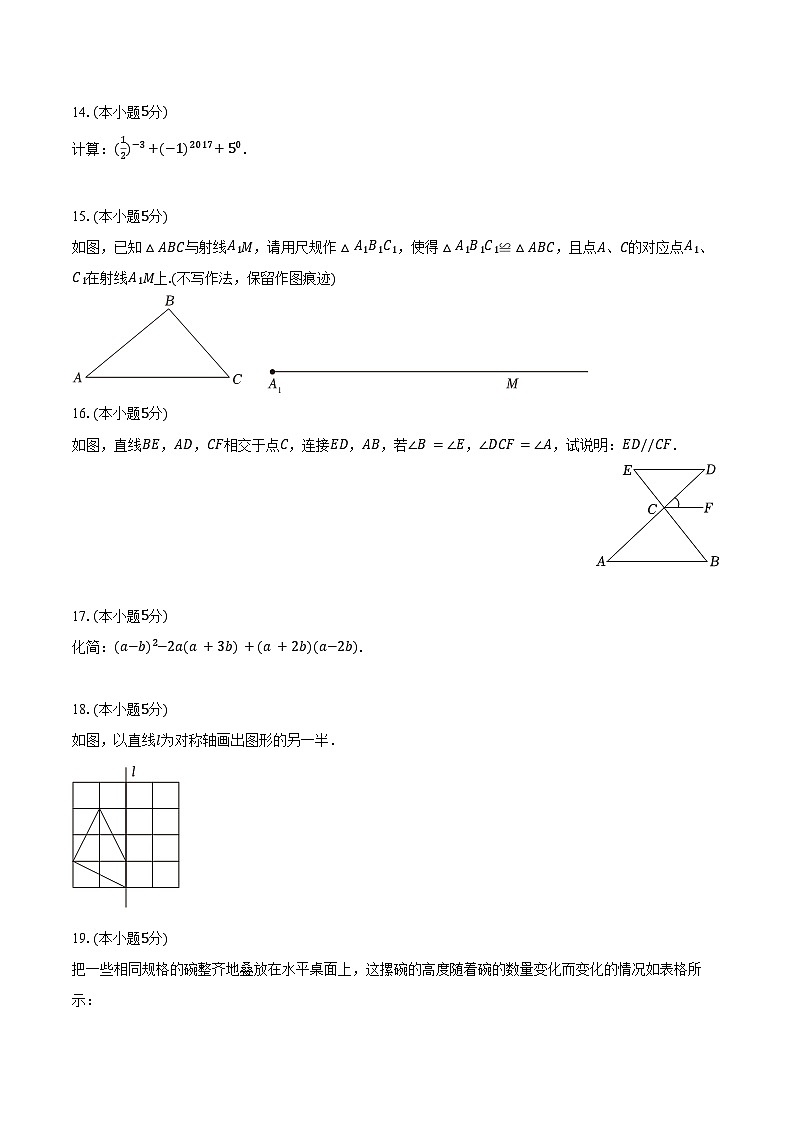
14.(本小题5分)
计算：(12)−3+(−1)2017+50．
15.(本小题5分)
如图，已知△ABC与射线A1M，请用尺规作△A1B1C1，使得△A1B1C1≌△ABC，且点A、C的对应点A1、C1在射线A1M上.(不写作法，保留作图痕迹)
16.(本小题5分)
如图，直线BE，AD，CF相交于点C，连接ED，AB，若∠B=∠E，∠DCF=∠A，试说明：ED//CF．
17.(本小题5分)
化简：(a−b)2−2a(a+3b)+(a+2b)(a−2b)．
18.(本小题5分)
如图，以直线l为对称轴画出图形的另一半．
19.(本小题5分)
把一些相同规格的碗整齐地叠放在水平桌面上，这摞碗的高度随着碗的数量变化而变化的情况如表格所示：
(1)上述两个变量之间的关系中，哪个是自变量？哪个是因变量？
(2)求当碗的数量为7时，这摞碗的高度．
20.(本小题5分)
已知一个不透明布袋里装有5个黑球，7个白球和4个蓝球，这些球除颜色外其余都相同.若搅匀后从该布袋里任意摸出1个球，求下面各事件的概率：
(1)摸出蓝球的概率；
(2)摸出不是白球的概率
21.(本小题6分)
如图，在△ABC中，E为AB上一点，连接CE，EC=BC，过点C作CD=AC，连接DE.且∠1=∠2.若∠B=75°，求∠3的度数．
22.(本小题7分)
如图，A、B、C、D是四个村庄，B、D、C三村在一条东西走向公路的沿线上，且D村到B村、C村的距离相等；村庄A、C，A、D间也有公路相连，且公路AD是南北走向；只有村庄A、B之间由于间隔了一个小湖，所以无直接相连的公路．现决定在湖面上造一座斜拉桥，测得AC=3千米，AE=1.2千米，BF=0.7千米．试求建造的斜拉桥至少有多少千米？
23.(本小题7分)
李老师为锻炼身体一直坚持步行上下班，一天早上李老师从家出发步行前往学校，途中遇到一位家长，同他聊了一会儿，之后便跑步到学校，这一过程李老师走过的路程y(米)与出发后时间x(分钟)关系如图所示．
(1)李老师家与学校距离为______米；李老师与家长聊天时间为______分钟；
(2)李老师的步行的速度是______米/分钟，跑步的速度是______米/分钟；
(3)如果李老师没有遇到家长，一直步行到校，那么她比实际情况早到多少分钟？
24.(本小题8分)
暑假将至，某商场为了吸引顾客，设立了一个可以自由转动的转盘(如图)，并规定：顾
客每购买300元的商品，就能获得一次转动转盘的机会，如果转盘停止后，指针正好对准红、黄或蓝色区域，顾客就可以分别获得100元、50元、20元的购物券(转盘被等分成16个扇形).若某顾客购物320元．
(1)求他获得购物券的概率；
(2)他获得哪种购物券的概率最大，并说明理由．
25.(本小题8分)
如图，在△ABC中，边AB的垂直平分线分别交BC，AB于点E，M，边AC的垂直平分线分别交BC，AC于点F，N，BE+FC=7．
(1)求AE+AF的长；
(2)若∠B+∠C=45°，AF=4.求△AEF的面积．
26.(本小题10分)
综合与探究
【操作探索】
在生活中，我们常用实物体验图形变换的过程.小颖同学利用一块风筝纸片完成了如下的操作：
如图1，已知四边形ABDC，AB=AC，BD=CD．
(1)操作一：沿AD所在的直线对折，如图1.你认为左右两侧对折后能完全重合吗？并说明理由；
(2)操作二：对折后，将风筝纸片剪成两个三角形(△ABD和△ACD′)，摆成如图2所示的图形，BD与AD′相交于点E，AD与CD′相交于点F.试说明BE=CF．
【应用拓展】
(3)如图3，在△ABC中，AB=AC，AB>BC，点D在边BC上，BD=3CD，点E，F在线段AD上，∠AEB=∠AFC=130°，∠BAC=50°，若△ABC的面积为24，求△ABE与△CDF的面积之和．
参考答案
1.C
2.C
3.A
4.C
5.C
6.D
7.C
8.B
9.随机
10.y=10x−x2
11.2.5
12.13或15
13.111°
14.解：原式=8−1+1
=8．
15.解：作图如下：

16.解：∵∠B=∠E，
∴AB//DE，
∵∠DCF=∠A，
∴AB//CF，
∴ED//CF．
17.解：原式=a2−2ab+b2−2a2−6ab+a2−4b2
=−8ab−3b2．
18.解：所作图形如图所示．

19.解：(1)上述两个变量之间的关系中，碗的数量是自变量，高度是因变量．
(2)由表格可知，增加1只碗，高度增加1.2cm，
4+1.2×(7−1)=11.2(cm)，
∴当碗的数量为7时，这摞碗的高度是11.2cm．
20.解：(1)∵布袋里装有5个黑球，7个白球和4个蓝球，
∴摸出蓝球的概率是45+7+4=14；
(2)摸出的不是白球的概率是5+45+7+4=916．
21.解：∵∠1=∠2，
∴∠1+∠ACE=∠2+∠ACE，
∴∠DCE=∠ACB，
在△DCE和△ACB中，
CD=AC∠DCE=∠ACBEC=BC，
∴△DCE≌△ACB(SAS)，
∴∠DEC=∠B=75°，
∵EC=BC，
∴∠CEB=∠B=75°，
∴∠DEB=∠DEC+∠CEB=150°，
∴∠3=180°−∠DEB=30°．
22.解：由题意，知
在△ADB与△ADC中
BD=CD∠BDA=∠CDA=90°AD=AD,
∴△ADB≌△ADC，
∴AB=AC=3，
故斜拉桥至少有3−1.2−0.7=1.1(千米)．
23.(1)1200；5；
(2)由李老师走过路程y(米)与出发后时间x(分钟)关系图可知，
李老师步行的速度为500÷5=100(米/分)；
李老师跑步的速度为(1200−500)÷(14−10)=175(米/分)，
答：步行速度100米/分；跑步的速度为175米/分．
(3)解：依题意，1200÷100=12(分)
14−12=2(分)
∴那么她比实际情况早到2分钟．
24.解：(1)获得购物券的概率=1+2+416=716；
(2)∵P(获得100元的概率)=116；
P(获得50元的概率)=216=18；
P(获得20元的概率)=416=14，
∵14>18>116，
∴他获得20元购物券的概率最大．
25.解：(1)∵ME是边AB的垂直平分线，NF是AC的垂直平分线，
∴BE=AE，FA=FC，
∴AE+AF=BE+FC=7；
(2)∵∠B+∠C=45°，
∴∠BAC=135°，
∵BE=AE，FA=FC，
∴∠EAB=∠B，∠FAC=∠C，
∴∠EAB+∠FAC=45°，
∴∠EAF=90°，
∵AF=4，
∴AE=3，
∴△AEF的面积=12AE×AF=12×3×4=6．
26.(1)解：能完全重合．理由如下：
在△ABD与△ACD中，
AB=ACBD=CDAD=AD，
∴△ABD≌△ACD(SSS)，
∴对折后能完全重合．
(2)证明：同理得出△ABD≌△ACD′，
∴∠B=∠C，∠BAD=∠CAD′，
∴∠BAD′+∠D′AD=∠CAD+∠D′AD，
∴∠BAE=∠CAF．
在△ABE和△ACF中，
∠B=∠CAB=AC∠BAE=∠CAF，
∴△ABE≌△ACF(ASA)，
∴BE=CF．
(3)解：∵∠AEB=130°，
∴∠EAB+∠ABE=180°−∠AEB=50°．
∵∠BAC=∠EAB+∠CAF=50°，
∴∠ABE=∠CAF．
在△ABE和△CAF中，
∠AEB=∠AFC∠ABE=∠CAFAB=AC，
∴△ABE≌△CAF(AAS)，
∴S△ABE=S△CAF，
∴S△ABE+S△CDF=S△CAF+S△CDF=S△CAD．
∵BD=3CD，
∴CD：BC=1：4，
∴S△CAD：S△ABC=CD：BC=1：4．
∵S△ABC=24，
∴S△ABE+S△CDF=24÷4=6．
试验次数
100
300
500
1000
1600
2000
“有2个人同月过生日”的次数
80
229
392
779
1251
1562
“有2个人同月过生日”的频率
0.8
0.763
0.784
0.779
0.782
0.781
碗的数量(只)
1
2
3
4
5
…
高度(cm)
4
5.2
6.4
7.6
8.8
…