2025年高考数学一轮复习-7.4-直线、平面垂直的判定与性质-专项训练【含解析】

这是一份2025年高考数学一轮复习-7.4-直线、平面垂直的判定与性质-专项训练【含解析】，共10页。

1.已知直线l1⊥平面α，直线l2⊂平面α，则l1与l2的位置关系一定成立的是（ ）
A.相交 B.垂直
C.异面 D.平行
2.如图，正方形SG1G2G3中，E，F分别是G1G2，G2G3的中点，D是EF的中点，现在沿SE，SF及EF把这个正方形折成一个四面体，使G1，G2，G3三点重合，重合后的点记为G，则在四面体S-EFG中必有（ ）
A.SG⊥△EFG所在平面
B.SD⊥△EFG所在平面
C.GF⊥△SEF所在平面
D.GD⊥△SEF所在平面
3.已知AB是圆柱上底面的一条直径，C是上底面圆周上异于A，B的一点，D为下底面圆周上一点，且AD⊥圆柱的底面，则必有（ ）
A.平面ABC⊥平面BCD
B.平面BCD⊥平面ACD
C.平面ABD⊥平面ACD
D.平面BCD⊥平面ABD
4.已知过平面α外一动点A的斜线l与平面α所成角为π6，并且斜线l交平面α于定点B，若动点A与平面α的距离为1，则斜线段AB在平面α上的射影所形成的图形面积是（ ）
A.3π B.2π
C.π D.π2
5.正六棱柱相邻两个侧面所成的二面角的大小为 .
.
1.已知m和n是两条不同的直线，α和β是两个不重合的平面，下面给出的条件中一定能推出m⊥β的是（ ）
A.α⊥β且m⊂α B.m⊥n且n∥β
C.m∥n且n⊥β D.m⊥n且α∥β
2.（多选）下列命题为真命题的是（ ）
A.若两个平面有无数个公共点，则这两个平面重合
B.一条直线垂直于两平行平面中的一个，则这条直线与另一个平面也垂直
C.垂直于同一条直线的两个平面相互平行
D.两个相交平面同时垂直于第三个平面，它们的交线也垂直于第三个平面
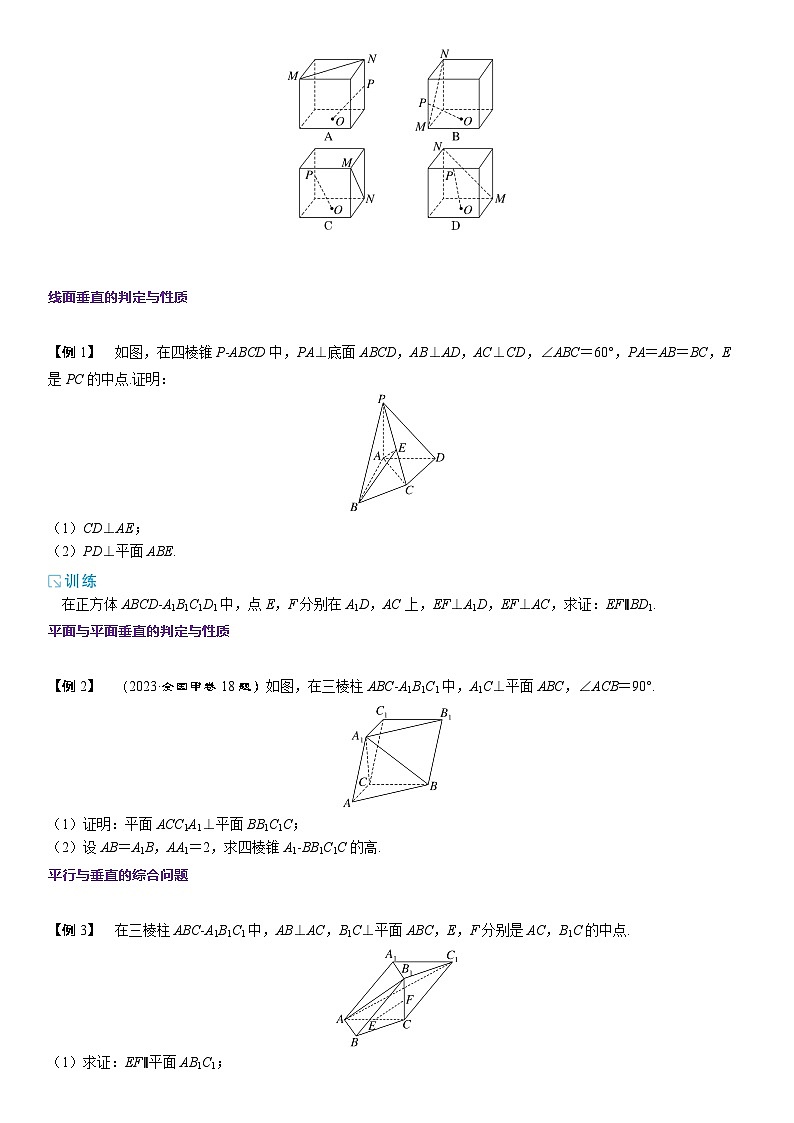
3.（多选）（2021·新高考Ⅱ卷10题）如图，在正方体中，O为底面的中心，P为所在棱的中点，M，N为正方体的顶点.则满足MN⊥OP的是（ ）
线面垂直的判定与性质
【例1】 如图，在四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点.证明：
（1）CD⊥AE；
（2）PD⊥平面ABE.
在正方体ABCD-A1B1C1D1中，点E，F分别在A1D，AC上，EF⊥A1D，EF⊥AC，求证：EF∥BD1.
平面与平面垂直的判定与性质
【例2】 （2023·全国甲卷18题）如图，在三棱柱ABC-A1B1C1中，A1C⊥平面ABC，∠ACB＝90°.
（1）证明：平面ACC1A1⊥平面BB1C1C；
（2）设AB＝A1B，AA1＝2，求四棱锥A1-BB1C1C的高.
平行与垂直的综合问题
【例3】 在三棱柱ABC-A1B1C1中，AB⊥AC，B1C⊥平面ABC，E，F分别是AC，B1C的中点.
（1）求证：EF∥平面AB1C1；
（2）求证：平面AB1C⊥平面ABB1.
【例4】 如图，在四棱锥P-ABCD中，底面ABCD为平行四边形，△PCD为等边三角形，平面PAC⊥平面PCD，PA⊥CD，CD＝2，AD＝3.
（1）设G，H分别为PB，AC的中点，求证：GH∥平面PAD；
（2）求证：PA⊥平面PCD；
（3）求直线AD与平面PAC所成角的正弦值.
（2022·全国甲卷19题）小明同学参加综合实践活动，设计了一个封闭的包装盒.包装盒如图所示：底面ABCD是边长为8（单位：cm）的正方形，△EAB，△FBC，△GCD，△HDA均为正三角形，且它们所在的平面都与平面ABCD垂直.
（1）证明：EF∥平面ABCD；
（2）求该包装盒的容积（不计包装盒材料的厚度）.
第四节 直线、平面垂直的判定与性质【解析版】

1.已知直线l1⊥平面α，直线l2⊂平面α，则l1与l2的位置关系一定成立的是（ ）
A.相交 B.垂直
C.异面 D.平行
解析：B 根据线面垂直的性质，则l1⊥l2，故选B.
2.如图，正方形SG1G2G3中，E，F分别是G1G2，G2G3的中点，D是EF的中点，现在沿SE，SF及EF把这个正方形折成一个四面体，使G1，G2，G3三点重合，重合后的点记为G，则在四面体S-EFG中必有（ ）
A.SG⊥△EFG所在平面
B.SD⊥△EFG所在平面
C.GF⊥△SEF所在平面
D.GD⊥△SEF所在平面
解析：A 四面体S-EFG如图所示，由SG⊥GE，SG⊥GF，且GE∩GF＝G得SG⊥△EFG所在的平面.故选A.
3.已知AB是圆柱上底面的一条直径，C是上底面圆周上异于A，B的一点，D为下底面圆周上一点，且AD⊥圆柱的底面，则必有（ ）
A.平面ABC⊥平面BCD
B.平面BCD⊥平面ACD
C.平面ABD⊥平面ACD
D.平面BCD⊥平面ABD
解析：B 因为AB是圆柱上底面的一条直径，所以AC⊥BC，又AD垂直于圆柱的底面，所以AD⊥BC，因为AC∩AD＝A，所以BC⊥平面ACD.由于BC⊂平面BCD.所以平面BCD⊥平面ACD.
4.已知过平面α外一动点A的斜线l与平面α所成角为π6，并且斜线l交平面α于定点B，若动点A与平面α的距离为1，则斜线段AB在平面α上的射影所形成的图形面积是（ ）
A.3π B.2π
C.π D.π2
解析：A 如图，过点A作平面α的垂线，垂足为C，连接BC，所以线段BC为线段AB在平面α上的射影，∠ABC为斜线l与平面α所成的角，则∠ABC＝π6，又AC＝1，所以BC＝3，故射影形成的图形为半径为3的圆面，其面积为3π.故选A.
5.正六棱柱相邻两个侧面所成的二面角的大小为 .
答案：2π3
解析：如图，由正六棱柱的几何特征可知BB'⊥AB，BB'⊥BC，则∠ABC为正六棱柱相邻两个侧面所成的二面角的平面角，∴∠ABC＝（6－2）π6＝2π3.
.
1.已知m和n是两条不同的直线，α和β是两个不重合的平面，下面给出的条件中一定能推出m⊥β的是（ ）
A.α⊥β且m⊂α B.m⊥n且n∥β
C.m∥n且n⊥β D.m⊥n且α∥β
解析：C 由结论1可知C正确.
2.（多选）下列命题为真命题的是（ ）
A.若两个平面有无数个公共点，则这两个平面重合
B.一条直线垂直于两平行平面中的一个，则这条直线与另一个平面也垂直
C.垂直于同一条直线的两个平面相互平行
D.两个相交平面同时垂直于第三个平面，它们的交线也垂直于第三个平面
解析：BCD 对于A，两个相交平面有一条交线，交线有无数个公共点，但是这两个平面不重合，故A错误；对于B，由结论3可知正确；对于C，由结论2可知正确；对于D，由结论4可知正确，故选B、C、D.
3.（多选）（2021·新高考Ⅱ卷10题）如图，在正方体中，O为底面的中心，P为所在棱的中点，M，N为正方体的顶点.则满足MN⊥OP的是（ ）
解析：BC 由结论5易知B、C正确.
线面垂直的判定与性质
【例1】 如图，在四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点.证明：
（1）CD⊥AE；
（2）PD⊥平面ABE.
证明：（1）在四棱锥P-ABCD中，
∵PA⊥底面ABCD，CD⊂平面ABCD，
∴PA⊥CD，
又∵AC⊥CD，且PA∩AC＝A，
∴CD⊥平面PAC.
又AE⊂平面PAC，∴CD⊥AE.
（2）由PA＝AB＝BC，∠ABC＝60°，可得AC＝PA.
∵E是PC的中点，∴AE⊥PC.
由（1）知AE⊥CD，且PC∩CD＝C，
∴AE⊥平面PCD.
又PD⊂平面PCD，∴AE⊥PD.
∵PA⊥底面ABCD，AB⊂平面ABCD，∴PA⊥AB.
又∵AB⊥AD，且PA∩AD＝A，
∴AB⊥平面PAD，
又PD⊂平面PAD，∴AB⊥PD.
又∵AB∩AE＝A，∴PD⊥平面ABE.
在正方体ABCD-A1B1C1D1中，点E，F分别在A1D，AC上，EF⊥A1D，EF⊥AC，求证：EF∥BD1.
证明：如图所示，连接A1C1，C1D，B1D1，BD.
∵AC∥A1C1，EF⊥AC，∴EF⊥A1C1.
又EF⊥A1D，A1D∩A1C1＝A1，
∴EF⊥平面A1C1D， ①
∵BB1⊥平面A1B1C1D1，A1C1⊂平面A1B1C1D1，∴BB1⊥A1C1.
∵四边形A1B1C1D1为正方形，∴A1C1⊥B1D1，
又B1D1∩BB1＝B1，∴A1C1⊥平面BB1D1D，
而BD1⊂平面BB1D1D，∴A1C1⊥BD1.同理DC1⊥BD1.
又DC1∩A1C1＝C1，∴BD1⊥平面A1C1D， ②
由①②可知EF∥BD1.
平面与平面垂直的判定与性质
【例2】 （2023·全国甲卷18题）如图，在三棱柱ABC-A1B1C1中，A1C⊥平面ABC，∠ACB＝90°.
（1）证明：平面ACC1A1⊥平面BB1C1C；
（2）设AB＝A1B，AA1＝2，求四棱锥A1-BB1C1C的高.
解：（1）证明：因为A1C⊥平面ABC，BC⊂平面ABC，所以A1C⊥BC.
因为∠ACB＝90°，所以AC⊥BC.
因为AC∩A1C＝C，AC，A1C⊂平面ACC1A1，
所以BC⊥平面ACC1A1.
因为BC⊂平面BB1C1C，
所以平面ACC1A1⊥平面BB1C1C.
（2）如图，取棱AA1的中点D，连接BD，CD.
因为AB＝A1B，所以AA1⊥BD.
因为BC⊥平面ACC1A1，AA1⊂平面ACC1A1，所以BC⊥AA1.
因为BC∩BD＝B，BC，BD⊂平面BCD，
所以AA1⊥平面BCD.
因为CD⊂平面BCD，所以AA1⊥CD.
因为AA1∥CC1，所以CD⊥CC1.
又因为CD⊥BC，BC∩CC1＝C，BC，CC1⊂平面BB1C1C，所以CD⊥平面BB1C1C.
因为AA1＝2，所以CD＝1.
易知AA1∥平面BB1C1C，
所以四棱锥A1-BB1C1C的高为CD＝1.
（2022·全国乙卷18题）如图，四面体ABCD中，AD⊥CD，AD＝CD，∠ADB＝∠BDC，E为AC的中点.
（1）证明：平面BED⊥平面ACD；
（2）设AB＝BD＝2，∠ACB＝60°，点F在BD上，当△AFC的面积最小时，求三棱锥F-ABC的体积.
解：（1）证明：因为AD＝CD，∠ADB＝∠BDC，DB＝DB，
所以△ADB≌△CDB，
所以BA＝BC，
又E为AC的中点，所以AC⊥BE，AC⊥DE，
因为BE∩DE＝E，且BE，DE⊂平面BED，所以AC⊥平面BED，
又AC⊂平面ACD，所以平面BED⊥平面ACD.
（2）由（1）可知BA＝BC，因为∠ACB＝60°，AB＝2，所以AC＝2，则BE＝3，DE＝1，
又BD＝2，所以BD2＝BE2＋DE2，所以DE⊥EB.
连接EF（图略），易知当△AFC的面积最小时，EF取最小值，
在Rt△BED中，EF的最小值为E到BD的距离，故当△AFC的面积最小时，EF＝DE·BEBD＝32.
由射影定理知EF2＝DF·FB，又DF＋FB＝BD＝2，所以DF＝12，FB＝32.
法一 因为DE⊥AC，DE⊥BE，AC∩BE＝E，所以DE⊥平面ABC，
则F到平面ABC的距离d＝BFBD×DE＝34.
故VF-ABC＝13S△ABC×d＝13×34×4×34＝34.
法二 由（1）知BD⊥AC，又BD⊥EF，所以BD⊥平面ACF，
所以BF即为B到平面ACF的距离，
故VF-ABC＝VB-AFC＝13S△AFC×BF＝13×12×AC×EF×BF＝34.
平行与垂直的综合问题
【例3】 在三棱柱ABC-A1B1C1中，AB⊥AC，B1C⊥平面ABC，E，F分别是AC，B1C的中点.
（1）求证：EF∥平面AB1C1；
（2）求证：平面AB1C⊥平面ABB1.
证明：（1）因为E，F分别是AC，B1C的中点，
所以EF∥AB1.
又EF⊄平面AB1C1，AB1⊂平面AB1C1，
所以EF∥平面AB1C1.
（2）因为B1C⊥平面ABC，AB⊂平面ABC，
所以B1C⊥AB.
又AB⊥AC，B1C⊂平面AB1C，AC⊂平面AB1C，B1C∩AC＝C，
所以AB⊥平面AB1C，
又因为AB⊂平面ABB1，
所以平面AB1C⊥平面ABB1.
【例4】 如图，在四棱锥P-ABCD中，底面ABCD为平行四边形，△PCD为等边三角形，平面PAC⊥平面PCD，PA⊥CD，CD＝2，AD＝3.
（1）设G，H分别为PB，AC的中点，求证：GH∥平面PAD；
（2）求证：PA⊥平面PCD；
（3）求直线AD与平面PAC所成角的正弦值.
解：（1）证明：连接BD，易知AC∩BD＝H，BH＝DH.
又由BG＝PG，故GH为△PBD的中位线，
所以GH∥PD.
又因为GH⊄平面PAD，PD⊂平面PAD，所以GH∥平面PAD.
（2）证明：取棱PC的中点N，连接DN.依题意，得DN⊥PC.
因为平面PAC⊥平面PCD，平面PAC∩平面PCD＝PC，DN⊂平面PCD，所以DN⊥平面PAC.
又PA⊂平面PAC，所以DN⊥PA.
又已知PA⊥CD，CD∩DN＝D，
所以PA⊥平面PCD.
（3）连接AN，由（2）中DN⊥平面PAC，可知∠DAN为直线AD与平面PAC所成的角.
因为△PCD为等边三角形，CD＝2，且N为PC的中点，所以DN＝3.
又DN⊥AN，在Rt△AND中，sin∠DAN＝DNAD＝33.
所以直线AD与平面PAC所成角的正弦值为33.
（2022·全国甲卷19题）小明同学参加综合实践活动，设计了一个封闭的包装盒.包装盒如图所示：底面ABCD是边长为8（单位：cm）的正方形，△EAB，△FBC，△GCD，△HDA均为正三角形，且它们所在的平面都与平面ABCD垂直.
（1）证明：EF∥平面ABCD；
（2）求该包装盒的容积（不计包装盒材料的厚度）.
解：（1）证明：如图，分别取AB，BC的中点M，N，连接EM，FN，MN，
∵△EAB与△FBC均为正三角形，且边长均为8，
∴EM⊥AB，FN⊥BC，且EM＝FN.
又平面EAB与平面FBC均垂直于平面ABCD，
平面EAB∩平面ABCD＝AB，平面FBC∩平面ABCD＝BC，EM⊂平面EAB，FN⊂平面FBC，
∴EM⊥平面ABCD，FN⊥平面ABCD，
∴EM∥FN，∴四边形EMNF为平行四边形，∴EF∥MN.
又MN⊂平面ABCD，EF⊄平面ABCD，
∴EF∥平面ABCD.
（2）如图，分别取AD，DC的中点P，Q，连接PM，PH，PQ，QN，QG，AC，BD.
由（1）知EM⊥平面ABCD，FN⊥平面ABCD，
同理可证得，GQ⊥平面ABCD，HP⊥平面ABCD，易得EM＝FN＝GQ＝HP＝43，EM∥FN∥GQ∥HP.
易得AC⊥BD，MN∥AC，PM∥BD，∴PM⊥MN，
又PM＝QN＝MN＝PQ＝12BD＝42，
∴四边形PMNQ是正方形，
∴四棱柱PMNQ-HEFG为正四棱柱，
∴V四棱柱PMNQ-HEFG＝（42）2×43＝1283.
∵AC⊥BD，BD∥PM，∴AC⊥PM.
∵EM⊥平面ABCD，AC⊂平面ABCD，∴EM⊥AC.
又EM，PM⊂平面PMEH，且EM∩PM＝M，∴AC⊥平面PMEH，
则点A到平面PMEH的距离d＝14AC＝22，
∴V四棱锥A-PMEH＝13S四边形PMEH×d＝13×42×43×22＝6433，
∴该包装盒的容积V＝V四棱柱PMNQ-HEFG＋4V四棱锥A-PMEH＝1283＋4×6433＝64033（cm3