
2025年高考数学一轮复习-8.7-利用空间向量研究距离问题-专项训练【含解析】
展开
这是一份2025年高考数学一轮复习-8.7-利用空间向量研究距离问题-专项训练【含解析】,共17页。
A. 22B. 32C. 62D. 3
2. 已知在三棱锥P−ABC中,PC⊥ 平面ABC,∠BAC=90∘ ,AB=AC=4,∠PBC=45∘ ,则点C到平面PAB的距离是( ).
A. 463B. 263C. 433D. 423
3. 已知在平行六面体ABCD−A1B1C1D1中,底面ABCD是边长为2的正方形,AA1=4,∠A1AD=∠A1AB=60∘ ,则异面直线AC与DC1所成的角的余弦值为( ).
A. 147B. 7014C. 31414D. 111414
4. 设α ,β ,γ 为平面,且α⊥β ,α∩β=l.若γ 与α 所成的二面角为45∘ ,l与γ 所成的角为30∘ ,则γ 与β 所成的锐二面角为( ).
A. 15∘B. 45∘C. 30∘D. 60∘
5. 在《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑,在鳖臑A−BCD中,AB⊥ 平面BCD,BC⊥CD,且AB=BC=CD,M为AD的中点,则异面直线BM与CD夹角的余弦值为( ).
A. 33B. 23C. 32D. 22
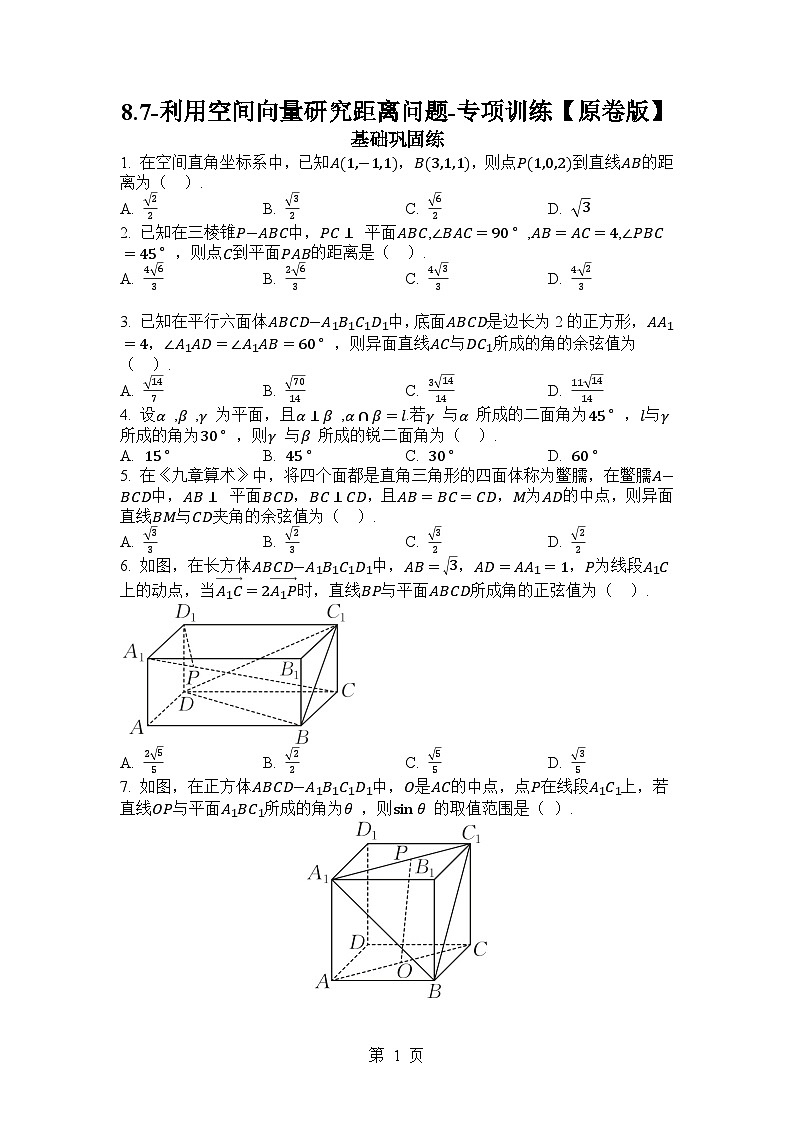
6. 如图,在长方体ABCD−A1B1C1D1中,AB=3,AD=AA1=1,P为线段A1C上的动点,当A1C=2A1P时,直线BP与平面ABCD所成角的正弦值为( ).
A. 255B. 22C. 55D. 35
7. 如图,在正方体ABCD−A1B1C1D1中,O是AC的中点,点P在线段A1C1上,若直线OP与平面A1BC1所成的角为θ ,则sin θ 的取值范围是( ).
A. [14,13]B. [13,12]C. [23,33]D. (23,33)
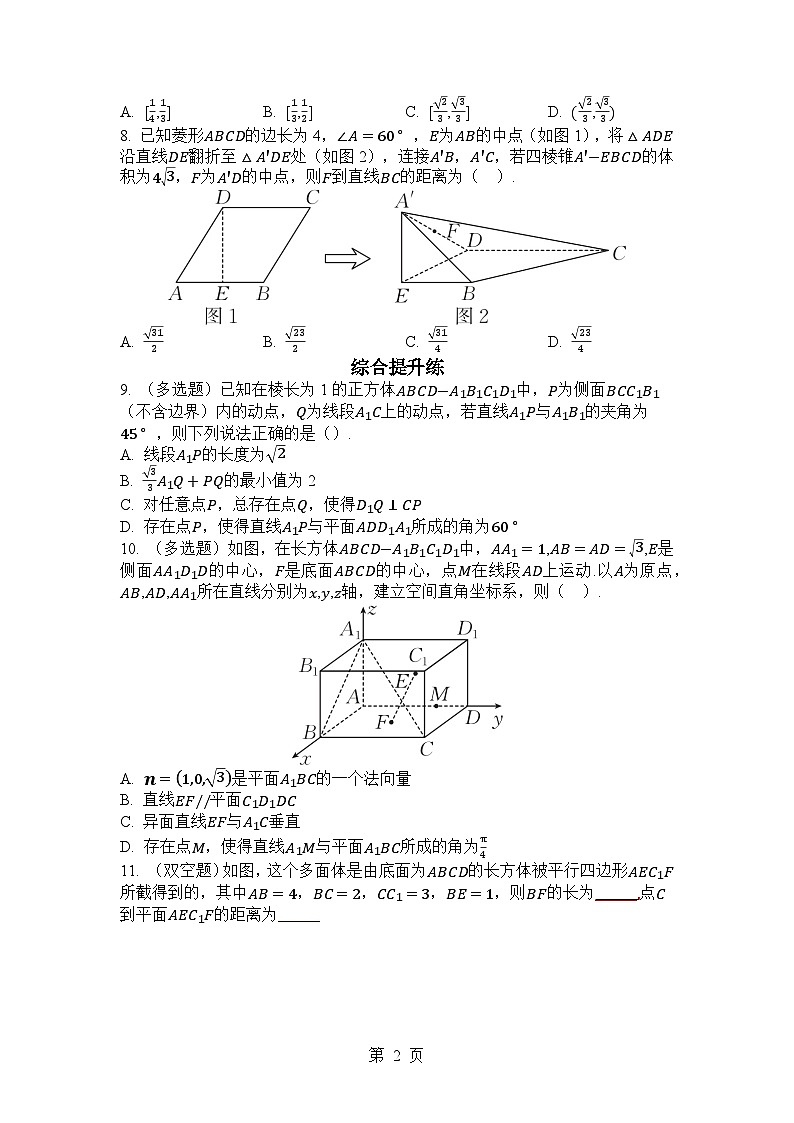
8. 已知菱形ABCD的边长为4,∠A=60∘ ,E为AB的中点(如图1),将△ADE沿直线DE翻折至△A'DE处(如图2),连接A'B,A'C,若四棱锥A'−EBCD的体积为43,F为A'D的中点,则F到直线BC的距离为( ).
A. 312B. 232C. 314D. 234
综合提升练
9. (多选题)已知在棱长为1的正方体ABCD−A1B1C1D1中,P为侧面BCC1B1(不含边界)内的动点,Q为线段A1C上的动点,若直线A1P与A1B1的夹角为45∘ ,则下列说法正确的是().
A. 线段A1P的长度为2
B. 33A1Q+PQ的最小值为2
C. 对任意点P,总存在点Q,使得D1Q⊥CP
D. 存在点P,使得直线A1P与平面ADD1A1所成的角为60∘
10. (多选题)如图,在长方体ABCD−A1B1C1D1中,AA1=1,AB=AD=3,E是侧面AA1D1D的中心,F是底面ABCD的中心,点M在线段AD上运动.以A为原点,AB,AD,AA1所在直线分别为x,y,z轴,建立空间直角坐标系,则( ).
A. n=1,0,3是平面A1BC的一个法向量
B. 直线EF//平面C1D1DC
C. 异面直线EF与A1C垂直
D. 存在点M,使得直线A1M与平面A1BC所成的角为π4
11. (双空题)如图,这个多面体是由底面为ABCD的长方体被平行四边形AEC1F所截得到的,其中AB=4,BC=2,CC1=3,BE=1,则BF的长为_______.点C到平面AEC1F的距离为_______
[
12. [2024·江苏模拟]如图,在三棱锥A−BCD中,已知CB=CD=5,BD=2,O为BD的中点,AO⊥ 平面BCD,AO=2,E为AC的中点.若点F在BC上,满足BF=14BC,则二面角F−DE−C的正弦值是_______
应用情境练
13. 钟鼓楼是中国传统建筑之一,属于钟楼和鼓楼的合称,是主要用于报时的建筑.中国古代一般建于城市的中心地带,在现代城市中,也常常可以看见附有钟楼的建筑.某建筑物楼顶有一顶部逐级收拢的四面钟楼,四个大钟对称分布在四棱柱的四个侧面(四棱柱看成正四棱柱,钟面圆心在棱柱侧面中心上),在整点时刻(在0点至12点中取整数点,含0点,不含12点),已知在3点时和9点时,相邻两钟面上的时针所在的两条直线相互垂直,则正面在2点时和右侧面在8点时,两钟面上的时针所在的两条直线所成的角的余弦值为_______
14.(2024·九省适应性测试)如图,在平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,O为AC与BD的交点,AA1=2,∠C1CB=∠C1CD,∠C1CO=45°.
(1)证明:C1O⊥平面ABCD.
(2)求二面角B-AA1-D的正弦值.
创新拓展练
15. 已知正方体ABCD−A1B1C1D1的内切球的表面积为π ,P是棱BB1上一动点,当直线C1D与平面A1C1P的夹角最大时,四面体D−A1C1P的体积为_______
.
16. [2024·青岛模拟]如图,P为圆锥的顶点,O为圆锥底面的圆心,圆锥的底面直径AB=4,母线PH=22,M是PB的中点,四边形OBCH为正方形.
(1)设平面POH∩ 平面PBC=l,证明:l//BC.
(2)设D为OH的中点,N是线段CD上的一点,当MN与平面PAB所成的角最大时,求MN的长.
8.7-利用空间向量研究距离问题-专项训练【解析版】
基础巩固练
1. 在空间直角坐标系中,已知A1,−1,1,B3,1,1,则点P1,0,2到直线AB的距离为( C ).
A. 22B. 32C. 62D. 3
[解析]∵A1,−1,1,B3,1,1,P1,0,2,
∴AB=2,2,0,AP=0,1,1,
∴AB⋅AP=2,AB=22,AP=2,
∴AP 在AB 方向上的投影向量的模ℎ=AB⋅APAB=222=22,
∴ 点P1,0,2 到直线AB 的距离d=AP2−ℎ2=2−12=62.故选C.
2. 已知在三棱锥P−ABC中,PC⊥ 平面ABC,∠BAC=90∘ ,AB=AC=4,∠PBC=45∘ ,则点C到平面PAB的距离是( A ).
A. 463B. 263C. 433D. 423
[解析]以A 为坐标原点,建立如图所示的空间直角坐标系,
则AP=0,4,42,AB=4,0,0,PC=0,0,−42.
设平面PAB 的一个法向量为m=x,y,z,
则m⋅AP→=0,m⋅AB→=0,
即4y+42z=0, 4x=0⇒y=−2z, x=0,
令y=2,则z=−1,
∴m=0,2,−1,∴ 点C 到平面PAB 的距离为PC⋅mm=463.
故选A.
3. 已知在平行六面体ABCD−A1B1C1D1中,底面ABCD是边长为2的正方形,AA1=4,∠A1AD=∠A1AB=60∘ ,则异面直线AC与DC1所成的角的余弦值为( C ).
A. 147B. 7014C. 31414D. 111414
[解析]如图,在平行六面体ABCD−A1B1C1D1 中,∠A1AD=∠A1AB=60∘ ,∠BAD=90∘ ,
DC1=AB+AA1,AD⋅AA1=AB⋅AA1=ABAA1cs∠A1AB=2×4cs 60∘=4,
则DC1=AB2+AA12+2AB⋅AA1=22+42+2×4=27,而AC=AB+AD,且AC=22,
于是AC⋅DC1=AB+AD⋅AB+AA1=AB2+AB⋅AD+AB⋅AA1+AD⋅AA1=4+4+4=12,
所以cs⟨AC,DC1⟩=AC⋅DC1ACDC1=1222×27=31414,
所以异面直线AC与DC1所成的角的余弦值为31414.故选C.
4. 设α ,β ,γ 为平面,且α⊥β ,α∩β=l.若γ 与α 所成的二面角为45∘ ,l与γ 所成的角为30∘ ,则γ 与β 所成的锐二面角为( D ).
A. 15∘B. 45∘C. 30∘D. 60∘
[解析]设平面α ,β ,γ 的单位法向量分别为a,b,c,直线l 上的单位方向向量为l.
根据题意,{a,b,l}构成空间直角坐标系的一个单位正交基底,
由题意可设c 与a 的夹角的余弦值为22,c与l 的夹角的余弦值为12,
设c=xa+yb+zl,c⋅a=x,则x=22,同理可得z=12,
由x2+y2+z2=1,解得y=±12,
于是所求锐二面角为60∘ .故选D.
5. 在《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑,在鳖臑A−BCD中,AB⊥ 平面BCD,BC⊥CD,且AB=BC=CD,M为AD的中点,则异面直线BM与CD夹角的余弦值为( A ).
A. 33B. 23C. 32D. 22
[解析]如图,正方体内的三棱锥A−BCD 为满足题意的鳖臑A−BCD,
以B 为原点,建立如图所示的空间直角坐标系,设正方体的棱长为1,
则B0,0,0,A0,0,1,C0,1,0,D1,1,0,M(12,12,12),
则BM=(12,12,12),CD=1,0,0,
cs⟨BM,CD⟩=BM⋅CDBM⋅CD=1234=33,
故异面直线BM 与CD 夹角的余弦值为33.故选A.
6. 如图,在长方体ABCD−A1B1C1D1中,AB=3,AD=AA1=1,P为线段A1C上的动点,当A1C=2A1P时,直线BP与平面ABCD所成角的正弦值为( C ).
A. 255B. 22C. 55D. 35
[解析]如图,以A 为坐标原点,AB,AD,AA1所在直线分别为x 轴、y轴、z轴建立空间直角坐标系.AB=3,AD=AA1=1,
则A10,0,1,B3,0,0,C3,1,0,C13,1,1,D0,1,0,D10,1,1,
设Px,y,z,则A1C=3,1,−1,A1P=x,y,z−1.
当A1C=2A1P 时,3=2x, 1=2y, −1=2z−1,
所以P(32,12,12),
所以BP=(−32,12,12),易知平面ABCD 的一个法向量为A1A=0,0,−1,
所以直线BP 与平面ABCD 所成角的正弦值为|cs⟨A1A,BP⟩=A1A⋅BPA1ABP=−1234+14+14|=55,故选C.
7. 如图,在正方体ABCD−A1B1C1D1中,O是AC的中点,点P在线段A1C1上,若直线OP与平面A1BC1所成的角为θ ,则sin θ 的取值范围是( C ).
A. [14,13]B. [13,12]C. [23,33]D. (23,33)
[解析]如图,设正方体的棱长为1,A1PA1C1=λ0≤λ≤1,则A1P=λA1C1,
连接B1D 并以D 为原点,DA,DC,DD1所在直线分别为x,y,z轴建立如图所示的空间直角坐标系,
则A1,0,0,C0,1,0,O(12,12,0),则A1C1=AC=−1,1,0,A1P=−λ,λ,0,又A11,0,1,所以P1−λ,λ,1,所以OP=(12−λ ,λ−12,1).
在正方体ABCD−A1B1C1D1 中,体对角线B1D⊥ 平面A1BC1,
所以DB1=1,1,1 是平面A1BC1 的一个法向量,
所以sin θ=|cs⟨OP,DB1⟩|
=12−λ+λ−12+13×12−λ2+λ−122+1
=16λ−122+3,
所以当λ=12 时,sin θ 取得最大值,最大值为33,当λ=0 或λ=1 时,sin θ 取得最小值,最小值为23,所以sin θ∈[23,33].故选C.
8. 已知菱形ABCD的边长为4,∠A=60∘ ,E为AB的中点(如图1),将△ADE沿直线DE翻折至△A'DE处(如图2),连接A'B,A'C,若四棱锥A'−EBCD的体积为43,F为A'D的中点,则F到直线BC的距离为( A ).
A. 312B. 232C. 314D. 234
[解析]连接BD(图略),因为四边形ABCD 为菱形,且∠A=60∘ ,所以△ABD 为等边三角形,
因为E 为AB 的中点,所以DE⊥AB,所以DE⊥EB,DE⊥A'E.
因为EB∩A'E=E,EB⊂ 平面A'EB,A'E⊂ 平面A'EB,所以DE⊥ 平面A'EB.
因为菱形ABCD 的边长为4,所以AB=AD=CD=BC=4,DE=23,AE=BE=2,
所以直角梯形BCDE 的面积为12×2+4×23=63,
设四棱锥A'−EBCD 的高为ℎ,则13×63ℎ=43,得ℎ=2,
所以ℎ=A'E,所以A'E⊥ 平面BCDE,
所以以E 为原点,ED,EB,EA'所在的直线分别为x,y,z轴,建立空间直角坐标系(图略),则B0,2,0,C23,4,0,A'0,0,2,F3,0,1,所以BC=23,2,0,
所以令c=BCBC=(32,12,0),a=FB=−3,2,−1,
所以a=3+4+1=22,a⋅c=−32+1=−12,
所以点F 到直线BC 的距离d=a2−a⋅c2=8−14=312.
故选A.
综合提升练
9. (多选题)已知在棱长为1的正方体ABCD−A1B1C1D1中,P为侧面BCC1B1(不含边界)内的动点,Q为线段A1C上的动点,若直线A1P与A1B1的夹角为45∘ ,则下列说法正确的是( AC ).
A. 线段A1P的长度为2
B. 33A1Q+PQ的最小值为2
C. 对任意点P,总存在点Q,使得D1Q⊥CP
D. 存在点P,使得直线A1P与平面ADD1A1所成的角为60∘
[解析]建立如图所示的空间直角坐标系D−xyz,根据题意,可得D0,0,0,A1,0,0,B1,1,0,C0,1,0,D10,0,1,A11,0,1,B11,1,1,C10,1,1,
设点Px1,1,z1,Qx2,y2,z2,由直线A1P 与A1B1 的夹角为45∘ ,得A1P=x1−1,1,z1−1,A1B1=0,1,0,
故cs 45∘=A1P⋅A1B1A1PA1B1,解得x1−12+z1−12=1.
Q为线段A1C 上的动点,则有A1Q=λA1C0≤λ≤1,解得Q1−λ,λ,1−λ.
对于A,有A1P=x1−12+z1−12+1=2,故A 正确;
对于B,过点Q 作平面ABCD 的垂线,垂足为R,
因为sin∠ACA1=AA1A1C=33,所以33A1Q=1−QR,
故求33A1Q+PQ 的最小值等价于求PQ−QR+1 的最小值,
因为QR=1−λ ,QP=1−λ−x12+λ−12+1−λ−z12,
所以QP2=1−λ−x12+λ−12+1−λ−z12≥λ−12=QR2,
则PQ−QR+1≥1,当且仅当x1=z1=1−λ 时,等号成立,结合x1−12+z1−12=1,可得此时λ=22,故B 错误;
对于C,若D1Q⊥CP,D1Q=1−λ,λ,−λ,CP=x1,0,z1,
则D1Q⋅CP=x11−λ−z1λ=0,又x1−12+z1−12=1,
所以当λ=1 时,D1Q⋅CP=−z=0,此时点P 与点B 重合,当点Q 与点C 重合时,P1Q⊥CP,当λ≠1 时,[λ2λ−12+1]z12+2λλ−1−2z1+1=0,则Δ=[2λλ−1−2]2−4[λ2λ−12+1]=−8λλ−1,
当0≤λ
相关试卷
这是一份2025高考数学一轮复习-7.6-利用空间向量求空间角、距离-专项训练【含解析】,共16页。试卷主要包含了已知直线l1的方向向量s1=,在空间直角坐标系中,已知A等内容,欢迎下载使用。
这是一份2025届高考数学一轮复习专练48 利用空间向量研究距离问题(Word版附解析),共17页。
这是一份2025高考数学一轮复习-7.6-利用空间向量求空间角、距离-专项训练【含解析】,共17页。









