2023-2024学年云南省昆明市八年级（下）期末数学试卷（含详细答案解析）

这是一份2023-2024学年云南省昆明市八年级（下）期末数学试卷（含详细答案解析），共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.下列二次根式中，是最简二次根式的是( )
A. 7B. 0.6C. 25D. 8
2.在英语听力口语考试中，7名女生的成绩如下：24，26，23，25，23，25，25，则这组数据的众数是( )
A. 28B. 22C. 23D. 25
3.一个直角三角形的两条直角边分别是6和8，斜边长是( )
A. 8B. 10C. 6D. 2 7
4.甲、乙、丙三个人进行篮球投球测试，他们的平均成绩相同，方差分别是：S甲2=0.61，S乙2=0.42，S丙2=0.54，则成绩最稳定的是( )
A. 甲B. 乙C. 丙D. 三个都一样
5.下列计算正确的是( )
A. 2+ 3= 5B. 3+ 3=3 3
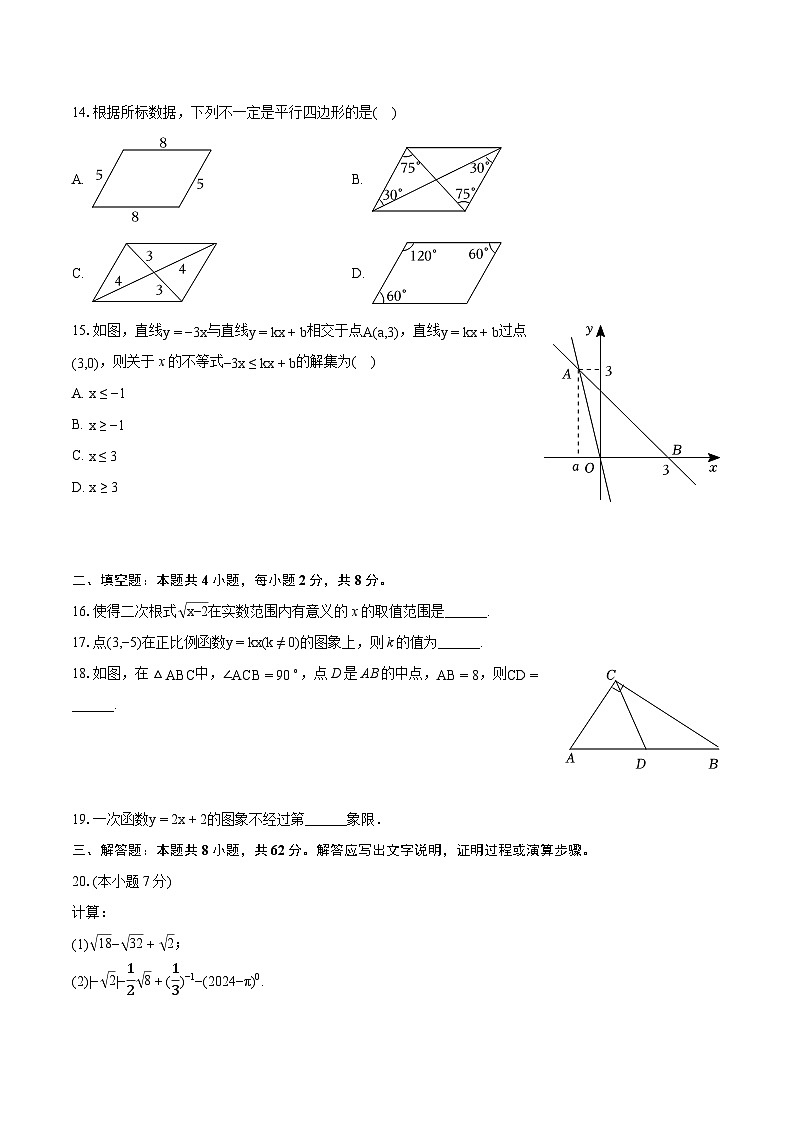
C. 8− 3= 5D. 3 2−2 2= 2
6.如图，两个一次函数图象的交点坐标为(2,4)，则关于x，y的方程组k1x+b1−y=0k2x+b2−y=0的解为( )
A. x=2y=4B. x=4y=2C. x=−4y=0D. x=3y=0
7.如图，A，B两点被池塘隔开，在AB外选一点C，连接AC，BC，并分别找出它们的中点D，E，连接DE，现测得DE=40m，则AB长为( )
A. 20m
B. 40m
C. 60m
D. 80m
8.要得到y=2x+2的图象，只需将y=2x( )
A. 向上平移2个单位B. 向下平移2个单位C. 向左平移2个单位D. 向右平移2个单位
9.在菱形ABCD中，若对角线AC=8，BD=6，则菱形ABCD的面积是( )
A. 48B. 24C. 20D. 14
10.如图，在正方形ABCD的外侧，作等边三角形DCE，连接AE，则∠ADE为( )
A. 120∘
B. 130∘
C. 150∘
D. 160∘
11.已知正比例函数y=(k−1)x，若y随x的增大而减小，则k的取值范围是( )
A. k1C. k0
12.下列图象中，不能表示y是x的函数的是( )
A. B. C. D.
13.如图，有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺.如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面.求这根芦苇的长度是多少尺？设芦苇的长度是x尺，根据题意，可列方程为( )
A. x2+52=102B. (10−1)2+52=x2
C. (x−1)2+52=x2D. x2+52=(x−1)2
14.根据所标数据，下列不一定是平行四边形的是( )
A. B.
C. D.
15.如图，直线y=−3x与直线y=kx+b相交于点A(a,3)，直线y=kx+b过点(3,0)，则关于x的不等式−3x≤kx+b的解集为( )
A. x≤−1
B. x≥−1
C. x≤3
D. x≥3
二、填空题：本题共4小题，每小题2分，共8分。
16.使得二次根式 x−2在实数范围内有意义的x的取值范围是______.
17.点(3,−5)在正比例函数y=kx(k≠0)的图象上，则k的值为______.
18.如图，在△ABC中，∠ACB=90∘，点D是AB的中点，AB=8，则CD=______.
19.一次函数y=2x+2的图象不经过第______象限．
三、解答题：本题共8小题，共62分。解答应写出文字说明，证明过程或演算步骤。
20.(本小题7分)
计算：
(1) 18− 32+ 2；
(2)|− 2|−12 8+(13)−1−(2024−π)0.
21.(本小题6分)
逸翠园中学八年级全体同学参加了某项捐款活动，随机抽取了部分同学捐款的情况进行统计，并绘制了两幅不完整统计图.
(1)求本次共抽查学生的人数，并将条形统计图补充完整；
(2)捐款金额的平均数是______，中位数是______；
(3)请你估算八年级800名学生中捐款大于等于20元的学生人数.
22.(本小题7分)
如图，点O是BD的中点，过点O作AC⊥BD，若AO=CO，连接AB，BC，CD，DA.求证：四边形ABCD是菱形.
23.(本小题6分)
如图，一个正比例函数与一个一次函数的图象交于点A(3,4)，其中一次函数与y轴交于B点，且OA=OB.
(1)求这两个函数的表达式；
(2)求△AOB的面积S.
24.(本小题8分)
如图，一个试验室在0：00−2：00保持20℃的恒温，在2：00−4：00匀速升温，每小时升高5℃.
(1)求出试验室温度T(单位： ℃)关于时间t(单位：h)的函数解析式.
(2)求实验室温度达到25℃时，是几时？
25.(本小题8分)
如图，在矩形ABCD中，对角线AC，BD相交于点O，分别过点A，C作AE⊥BD于点E，CF⊥BD于点F，连接AF，CE.
(1)求证：四边形AECF是平行四边形；
(2)若AB=1，BE=EO，求BC的长.
26.(本小题8分)
某房地产开发公司计划建A、B两种户型的经济适用住房共80套，该公司所筹资金不少于2090万元但不超过2096万元，且所筹资金全部用于建房，两种户型的建房成本和售价如表：
(1)该公司对这两种户型住房有哪几种建房方案？
(2)若该公司所建的两种户型住房可全部售出.请问哪一种建房方案获得利润最大？并求出最大利润.
27.(本小题12分)
综合与实践
【教材情境】
数学活动课上，老师提出这样一个问题：在八年级上册我们遇到了这样一个问题，如图，△ABD和△AEC都是等边三角形.求证BE=DC.
我们可以证明△ACD≌△AEB，得到BE=DC.
【观察思考】
在八年级下册，我们学习了平行四边形这一章后，有如下问题：如图①，在正方形ABCD中，以CP为边在正方形ABCD外作矩形PCEF，连接AP，DE，且BP=DE.
(1)我们能从以上【教材情境】得到启发，证明矩形PCEF是正方形，请写出证明过程.
【实践探究】
(2)希望小队提出：若P是CD边上一个动点(P与C，D不重合)，在图①中，连接AP，当点P在什么位置时，AP=DE，请写出证明过程.
【拓展迁移】
(3)冲锋小队再次提出：若将图①中的正方形PCEF绕点C按顺时针方向旋转任意角度，得到图②的情形(BP与CD交于点G，与DE交于点O)，此时，请猜想图②中线段BP与线段DE的关系？请写出你的猜想结果，并证明你所得到的结论.
答案和解析
1.【答案】A
【解析】解：∵ 7是最简二次根式，
∴选项A符合题意；
∵ 0.6= 35= 155，
∴选项B不符合题意；
∵ 25= 105，
∴选项C不符合题意；
∵ 8=2 2，
∴选项D不符合题意，
故选：A.
运用最简二次根式的定义和化简方法进行逐一辨别．
此题考查了最简二次根式的辨别能力，关键是能准确理解并运用最简二次根式的定义和化简方法．
2.【答案】D
【解析】解：这组数据24，26，23，25，23，25，25中，25出现的次数最多，
∴这组数据的众数是25，
故选：D.
根据众数的定义的解答．
此题考查了众数定义，掌握众数的定义是解题的关键．
3.【答案】B
【解析】解：∵一个直角三角形的两条直角边分别是6和8，
∴斜边长是： 62+82=10.
故选：B.
利用勾股定理直接解答即可．
本题考查勾股定理的应用．解题的关键掌握勾股定理．
4.【答案】B
【解析】解：∵S甲2=0.61，S乙2=0.42，S丙2=0.54，
∴S乙2