2023-2024学年四川省眉山市仁寿县八年级（下）期末数学试卷（含详细答案解析）

这是一份2023-2024学年四川省眉山市仁寿县八年级（下）期末数学试卷（含详细答案解析），共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.18的立方根是( )
A. −12B. ±12C. 12D. 14
2.下列计算正确的是( )
A. m2+2m2=3m4B. m5⋅m2=m10
C. (3mn)2=6m2n2D. 4m3÷2m=2m2
3.估计 5−1的值应在( )
A. 0和1之间B. 1和2之间C. 3和4之间D. 5和6之间
4.下列等式从左到右的变形，属于因式分解的是( )
A. a(x−y)=ax−ayB. x2+2x+1=x(x+2)+1
C. x2−4y2=(x+4y)(x−4y)D. x3−x=x(x+1)(x−1)
5.下列因式分解错误的是( )
A. 8a−4b+12=4(2a−b+3)B. 4a2+4a+1=(2a+1)2
C. m2−n2=(m+n)(m−n)D. x2+y2=(x+y)2
6.下列判断中错误的是( )
A. 有两角和一边对应相等的两个三角形全等
B. 有两边和一角对应相等的两个三角形全等
C. 有两边和其中一边上的中线对应相等的两个三角形全等
D. 有一边对应相等的两个等边三角形全等
7.如图，在等边三角形ABC中，AD⊥BC，垂足为D，点E在线段AD上，∠EBC=45∘，则∠ACE等于( )
A. 18∘
B. 20∘
C. 30∘
D. 15∘
8.下列命题的逆命题是假命题的是( )
A. 关于某一条直线对称的两个三角形全等
B. 到线段两端点距离相等的点在线段的垂直平分线上
C. 在一个角的内部，在角平分线上的点到这个角两边的距离相等
D. 直角三角形两直角边的平方和等于斜边的平方
9.如图所示，是巴中某校对学生到校方式的情况统计图．若该校骑自行车到校的学生有200人，则步行到校的学生有( )
A. 120人
B. 160人
C. 125人
D. 180人
10.如图，已知△ABC的面积为8，在BC上截取BD=BA，作∠ABC的平分线交AD于点P，连接PC，则△BPC的面积为( )
A. 2
B. 4
C. 5
D. 6
11.已知(x−2020)2+(x−2022)2=18，则(x−2021)2的值是( )
A. 4B. 8C. 12D. 16
12.如图，在△ABC中，∠C=90∘，AD平分∠BAC，DE⊥AB于E，则下列结论：
①DA平分∠CDE；②∠BAC=∠BDE；③DE平分∠ADB；④BE+AC=AB；⑤A、D两点一定在线段EC的垂直平分线上，其中正确的有( )
A. 2个B. 3个C. 4个D. 5个
二、填空题：本题共6小题，每小题4分，共24分。
13.因式分解a2+a−6的结果是______.
14.已知a2+14b2=2a−b−2，则3a−12b的值为______.
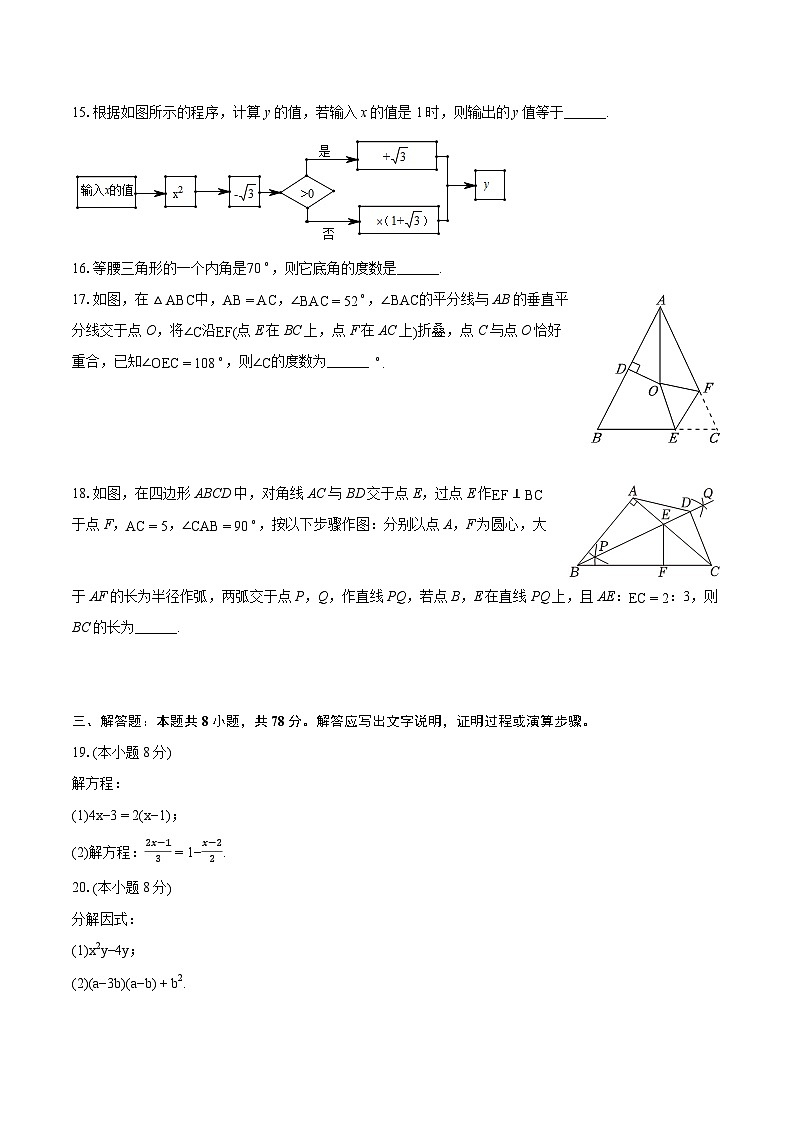
15.根据如图所示的程序，计算y的值，若输入x的值是1时，则输出的y值等于______.
16.等腰三角形的一个内角是70∘，则它底角的度数是______.
17.如图，在△ABC中，AB=AC，∠BAC=52∘，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF(点E在BC上，点F在AC上)折叠，点C与点O恰好重合，已知∠OEC=108∘，则∠C的度数为______ ∘.
18.如图，在四边形ABCD中，对角线AC与BD交于点E，过点E作EF⊥BC于点F，AC=5，∠CAB=90∘，按以下步骤作图：分别以点A，F为圆心，大于AF的长为半径作弧，两弧交于点P，Q，作直线PQ，若点B，E在直线PQ上，且AE：EC=2：3，则BC的长为______.
三、解答题：本题共8小题，共78分。解答应写出文字说明，证明过程或演算步骤。
19.(本小题8分)
解方程：
(1)4x−3=2(x−1)；
(2)解方程：2x−13=1−x−22.
20.(本小题8分)
分解因式：
(1)x2y−4y；
(2)(a−3b)(a−b)+b2.
21.(本小题10分)
已知：a+b=4，ab=1.求：
①a2+b2的值；
②a−b的值．
22.(本小题10分)
一个工人拿一个2.5米长的梯子，底端放在离墙脚0.7米处，另一端靠墙，如果梯子的顶部下滑0.4米，那么梯子的底部向外滑了多少米？
23.(本小题12分)
(1)【案例展示】如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45∘，连接EF，则EF=BE+DF，理由如下：
∵AB=AD，可把△ABE绕点A逆时针旋转90∘至△ADG，可使AB与AD重合，
∵∠ADC=∠B=∠ADG=90∘，
∴∠FDG=180∘，点F、D、G共由旋转得：△ABE≌△ADG，
∴AE=AG，BE=DG，∠BAE=∠DAG，而∠BAE+∠DAF=∠BAD−∠EAF=90∘−45∘=45∘，
∴∠DAG+∠DAF=∠FAG=45∘45∘即∠EAF=∠FAG，
∴______≌△AFG，根据是______(第一空填三角形，第二空填全等的依据)，
∴EF=FG，
又∵FG=DG+DF，
∴EF=DG+DF=BE+DF.
(2)【类比引申】如图2，四边形ABCD中，AB=AD，∠BAD=90∘点E、F分别在边BC、CD上，∠EAF=45∘.若∠B、∠D都不是直角时EF=BE+DF仍成立，则∠B与∠D应该满足什么数量关系是______.
(3)【拓展运用】如图3，在△ABC中，∠BAC=90∘，AB=AC，点D、E均在边BC上，且∠DAE=45∘.猜想BD、DE、EC应满足的等量关系，并写出推理过程.
24.(本小题12分)
如图，在△ABC中，AB=AC=2，∠B=∠C=40∘，点D在线段BC上运动(D不与B、C重合)，连接AD，作∠ADE=40∘，DE交线段AC于E.
(1)当∠BDA=115∘时，∠EDC=________ ∘，∠DEC=________ ∘；点D从B向C运动时，∠BDA逐渐变________(填“大”或“小”)；
(2)当DC等于多少时，△ABD≌△DCE，请说明理由；
(3)在点D的运动过程中，△ADE的形状可以是等腰三角形吗？若可以，请直接写出∠BDA的度数．若不可以，请说明理由．
25.(本小题10分)
化简a2−4a+4a2−4÷a−2a2+2a，并从−2、0、1、2中选一个数作为a的值代入求值.
26.(本小题8分)
如图，在平面直角坐标系中，描出下列各点：A(4,3)，B(−2,3)，C(−4,−1)，D(2,−2)，并写出图中E，F，G，H各点的坐标.
答案和解析
1.【答案】C
【解析】解：∵(12)3=18，
∴18的立方根是12.
故选：C.
根据立方根的定义，如果一个数x的立方等于a，则这个数x就是a的立方根．
本题考查了立方根的定义，充分理解立方根的定义并能熟练应用是解答本题的关键．
2.【答案】D
【解析】解：A、原式=3m2，故A选项错误．
B、原式=m7，故B选项错误．
C、原式=9m2n2，故C选项错误．
D、原式=2m2，故D选项正确．
故选：D.
根据整式的运算法则即可求出答案．
本题考查整式的运算法则，解题的关键是熟练运用整式的运算法则，本题属于基础题型．
3.【答案】B
【解析】解：∵22=4，32=9，
∴2< 5