
2023-2024学年贵州省遵义市八年级(下)期末数学试卷(含详细答案解析)
展开1.下列四个式子中,最简二次根式为( )
A. (−2)2B. 12C. 34D. 7
2.点(3,−5)在正比例函数y=kx(k≠0)的图象上,则k的值为( )
A. −15B. 15C. −35D. −53
3.某校举办“强国复兴有我,争做新时代美德少年”演讲比赛.比赛中,九位评委给某个选手打分,如果去掉一个最高分和一个最低分,则下列数据一定不发生变化的是( )
A. 方差B. 平均数C. 众数D. 中位数
4.下列计算正确的是( )
A. 5− 3= 2B. 2+ 2=2 2C. 2× 3= 6D. 6÷ 3= 3
5.在平行四边形ABCD中,∠A:∠B:∠C:∠D的值可以是( )
A. 1:2:1:2B. 1:2:2:1C. 1:2:3:4D. 1:1:2:2
6.如图,在菱形ABCD中,对角线AC与BD相交于点O,∠ABC=120∘,BD=4,则对角线AC的长为( )
A. 4 3
B. 2 3
C. 4
D. 8
7.如图在一个高为3米,长为5米的楼梯表面铺地毯,则地毯至少需要( )
A. 3米B. 4米C. 5米D. 7米
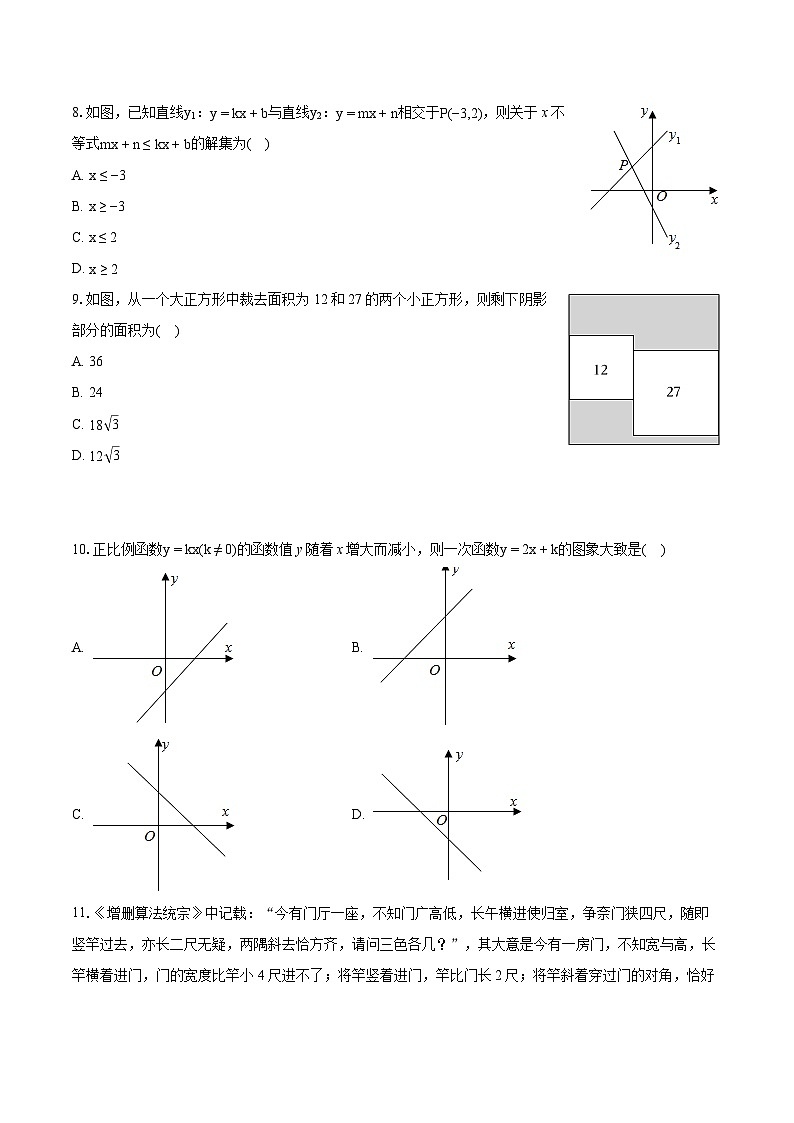
8.如图,已知直线y1:y=kx+b与直线y2:y=mx+n相交于P(−3,2),则关于x不等式mx+n≤kx+b的解集为( )
A. x≤−3
B. x≥−3
C. x≤2
D. x≥2
9.如图,从一个大正方形中裁去面积为12和27的两个小正方形,则剩下阴影部分的面积为( )
A. 36
B. 24
C. 18 3
D. 12 3
10.正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=2x+k的图象大致是( )
A. B.
C. D.
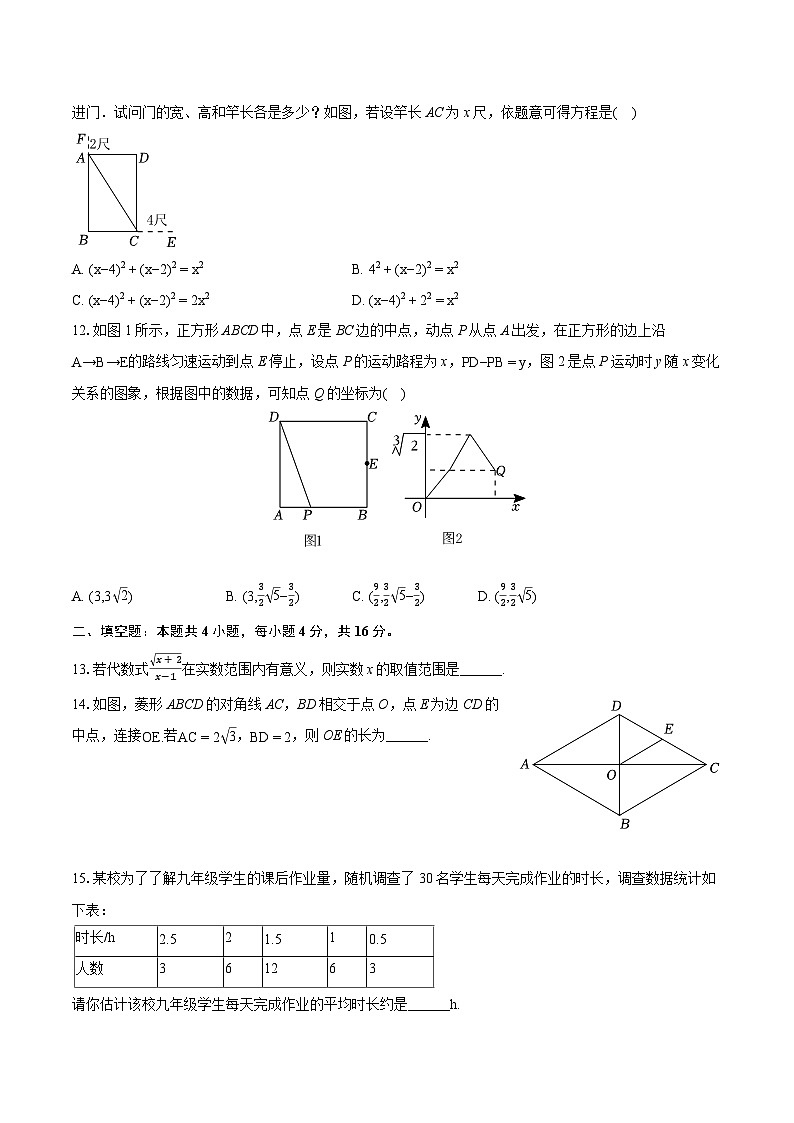
11.《增删算法统宗》中记载:“今有门厅一座,不知门广高低,长午横进使归室,争奈门狭四尺,随即竖竿过去,亦长二尺无疑,两隅斜去恰方齐,请问三色各几?”,其大意是今有一房门,不知宽与高,长竿横着进门,门的宽度比竿小4尺进不了;将竿竖着进门,竿比门长2尺;将竿斜着穿过门的对角,恰好进门.试问门的宽、高和竿长各是多少?如图,若设竿长AC为x尺,依题意可得方程是( )
A. (x−4)2+(x−2)2=x2B. 42+(x−2)2=x2
C. (x−4)2+(x−2)2=2x2D. (x−4)2+22=x2
12.如图1所示,正方形ABCD中,点E是BC边的中点,动点P从点A出发,在正方形的边上沿A→B→E的路线匀速运动到点E停止,设点P的运动路程为x,PD−PB=y,图2是点P运动时y随x变化关系的图象,根据图中的数据,可知点Q的坐标为( )
A. (3,3 2)B. (3,32 5−32)C. (92,32 5−32)D. (92,32 5)
二、填空题:本题共4小题,每小题4分,共16分。
13.若代数式 x+2x−1在实数范围内有意义,则实数x的取值范围是______.
14.如图,菱形ABCD的对角线AC,BD相交于点O,点E为边CD的中点,连接OE.若AC=2 3,BD=2,则OE的长为______.
15.某校为了了解九年级学生的课后作业量,随机调查了30名学生每天完成作业的时长,调查数据统计如下表:
请你估计该校九年级学生每天完成作业的平均时长约是______h.
16.一次函数y=kx+b(k≠0)的图象由函数y=x的图象平移得到,且经过点(1,3).当x>1时,对于x的每一个值,函数y=mx(m≠0)的值大于一次函数y=kx+b的值,直接写出m的取值范围______.
三、解答题:本题共9小题,共98分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题10分)
(1)计算: 16÷2− 13× 6−(− 3)0.
(2)先化简,再求值:(2x− 5)(2x+ 5)−4x(x−2),其中x= 3+1.
18.(本小题10分)
某校举办国学知识竞赛,设定满分10分,学生得分均为整数.在初赛中,甲、乙两组(每组10人)学生成绩如下:(单位:分)
甲组:5,6,6,6,6,6,7,9,9,10.
乙组:5,6,6,6,7,7,7,7,9,10.
(1)以上成绩统计分析表中a=______,b=______,c=______;
(2)小明同学说:“这次竞赛我得了7分,在我们小组中属中游略偏上!”观察上面表格判断,小明可能是______组的学生;
(3)从平均数和方差看,若从甲乙两组学生中选择一个组参加决赛,应选哪个组?并说明理由.
19.(本小题10分)
如图,网格中每个小正方形的边长都是1,点A、B、C、D都在格点上.
(1)线段AB的长度是______,线段 CD的长度是______.
(2)若EF的长为 5,那么以AB、CD、EF三条线段为边能否构成直角三角形,并说明理由.
20.(本小题10分)
如图,在四边形ABCD中,AB//CD,点E,F在对角线BD上,BE=EF=FD,∠BAF=∠DCE=90∘.
(1)求证:△ABF≌△CDE;
(2)连接AE,CF,请从以下两个条件中选择一个作为已知条件,判断四边形AECF的形状,我选序号:______,条件①:∠ABD=30∘;条件②:AB=BC.
(注:如果选择条件①条件②分别进行解答,按第一个解答计分)
21.(本小题10分)
我国传统的计重工具-秤的应用,方便了人们的生活.如图1,可以用秤砣到秤纽的水平距离,来得出秤钩上所挂物体的重量.称重时,若秤杆上秤砣到秤纽的水平距离为x(厘米)时,秤钩所挂物重为y(斤),则y是x的一次函数.下表中为若干次称重时所记录的一些数据.
(1)在上表x,y的数据中,发现有一对数据记录错误.在图2中,通过描点的方法,观察判断哪一对是错误的?
(2)根据(1)的发现,问秤杆上秤砣到秤纽的水平距离为18厘米时,秤钩所挂物重是多少?
22.(本小题12分)
小明学习菱形时,对矩形ABCD进行了画图探究(AD>AB),其作法和图形如下:
①连接BD;
②分别以点B,D为圆心,大于BD长的一半为半径作弧,两弧相交于M,N两点,作直线MN交BD于点O,交AD于点E,交BC于点F;
③连接BE,DF.
(1)根据以上作法,判断四边形BFDE的形状,并说明理由;
(2)若AB=4,AD=8,求四边形BFDE的面积.
23.(本小题12分)
小王是“新星厂”的一名工人,请你阅读下列信息:
信息一:工人工作时间:每天上午8:00−12:00,下午14:00−18:00,每月工作25天;
信息二:小王生产甲、乙两种产品的件数与所用时间的关系见下表:
信息三:按件计酬,每生产一件甲种产品得1.50元,每生产一件乙种产品得2.80元.
信息四:该厂工人每月收入由底薪和计酬工资两部分构成,小王每月的底薪为1900元,请根据以上信息,解答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分钟;
(2)2018年1月工厂要求小王生产甲种产品的件数不少于60件,则小王该月收入最多是多少元?此时小王生产的甲、乙两种产品分别是多少件?
24.(本小题12分)
如图,直线l1:y=x+3与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B.
(1)求直线l2的解析式;
(2)过动点P(n,0)且垂直于x轴的直线与l1,l2的交点分别为M,N,当点M位于点N上方时.
①请直接写出n的取值范围______;
②若MN=AB,求点M的坐标.
25.(本小题12分)
综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作判断
操作一:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;
操作二:在AD上选一点P,连接BP,沿BP折叠,使点A落在矩形内部点M处,把纸片展平,连接PM,BM.
如图1,当点M在EF上时,根据以上操作,写出一个度数为30∘的角为______;
(2)迁移探究
小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片ABCD按照(1)中的方式操作,并延长PM交CD于点Q,连接BQ.
①如图2,当点M在EF上时,则∠MBQ=______;
②改变点P在AD上的位置(点P不与点A,D重合)如图3,判断∠MBQ与∠CBQ的数量关系,并说明理由;
(3)拓展应用
在(2)的探究中,已知正方形纸片ABCD的边长为8cm,当FQ=1cm时,请直接写出AP的长.
答案和解析
1.【答案】D
【解析】解:A、 (−2)2=2,故A不符合题意;
B、 12=2 3,故B不符合题意;
C、 34= 32,故C不符合题意;
D、 7是最简二次根式,故D符合题意;
故选:D.
根据最简二次根式的定义:被开方数中不含能开得尽方的因数或因式,被开方数中不含分母,逐一判断即可解答.
本题考查了最简二次根式,熟练掌握最简二次根式的定义是解题的关键.
2.【答案】D
【解析】【分析】
此题主要考查了待定系数法求正比例函数解析式,正确得出k的值是解题关键.
直接把已知点代入,进而求出k的值.
【解答】
解:∵点(3,−5)在正比例函数y=kx(k≠0)的图象上,
∴−5=3k,
解得:k=−53,
故选:D.
3.【答案】D
【解析】解:去掉一个最高分和一个最低分,平均分、众数、方差可能发生变化,
中位数一定不发生变化,
故选:D.
根据平均数、中位数、众数、方差的定义判断即可.
此题主要考查了中位数、众数、算术平均数、方差的含义和判断,要熟练掌握,解答此题的关键是要明确:中位数代表了这组数据值大小的“中点”,不易受极端值影响.
4.【答案】C
【解析】解:A、 5− 3≠ 2,故选项A不符合题意;
B、2+ 2≠2 2,故选项B不符合题意;
C、 2× 3= 6,故选项C符合题意;
D、 6÷ 3= 2,故选项D不符合题意;
故选:C.
根据二次根式的混合运算法则计算并判断即可.
本题考查的是二次根式的混合运算,熟练掌握其运算法则是解题的关键.
5.【答案】A
【解析】【分析】
本题考查了平行四边形的对角相等的性质;熟练掌握平行四边形的性质是解决问题的关键.根据平行四边形的对角相等,容易得出结论.
【解答】
解:∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D,
∴A正确,
故选A.
6.【答案】A
【解析】解:在菱形ABCD中,对角线AC与BD相交于点O,∠ABC=120∘,BD=4,
∴∠BAD=60∘,AD=AB,
则△ABD是等边三角形,
∴AB=AD=CD=BC=4,∠DAC=12∠BAD=30∘,
故AO=4cs30∘=2 3,
∴AC=2AO=4 3.
故选:A.
根据菱形的性质结合等边三角形的判定与性质得出△ABD是等边三角形,可求出AD的长,再根据特殊角的锐角三角函数值进而求出AC的长.
此题主要考查了菱形的性质以及等边三角形的判定与性质,求出OA的长是解题关键.
7.【答案】D
【解析】解:由勾股定理得:
楼梯的水平宽度= 52−32=4(米),
∵地毯铺满楼梯的长度应该是楼梯的水平宽度与垂直高度的和,
∴地毯的长度至少是3+4=7(米).
故选:D.
当地毯铺满楼梯时的长度是楼梯的水平宽度与垂直高度的和,根据勾股定理求得水平宽度,即可求得地毯的长度.
此题考查了生活中的平移现象以及勾股定理,属于基础题,利用勾股定理求出水平边的长度是解答本题的关键.
8.【答案】B
【解析】解:∵直线y1:y=kx+b与直线y2:y=mx+n相交于P(−3,2),
∴不等式mx+n≤kx+b的解为:x≥−3.
故选:B.
根据函数图象交点右侧直线y2:y=mx+n图象在直线y1:y=kx+b图象的下面,即可得出不等式mx+n≤kx+b的解集.
此题主要考查了一次函数与不等式,利用数形结合得出不等式的解集是考试重点.
9.【答案】A
【解析】解:∵两个小正方形面积分别为12和27,
∴两个小正方形的边长分别为 12=2 3和 27=3 3,
∴大正方形的边长为:2 3+3 3=5 3,
∴S阴影=(5 3)2−12−27=75−12−27=36,故A正确.
故选:A.
先求出两个小正方形的边长,然后再求出大正方形的边长,用大正方形的面积减去两个小正方形的面积即可.
本题主要考查了二次根式的应用,二次根式的性质,解题的关键是求出大正方形的边长,准确计算.
10.【答案】A
【解析】解:∵正比例函数y=kx(k≠0)的函数值y随x的增大而减小,
∴k<0,
∵一次函数y=2x+k的一次项系数大于0,常数项小于0,
∴一次函数y=x+k的图象经过第一、三、四象限,
故选:A.
根据正比例函数的性质得到k<0,然后根据一次函数的性质得到一次函数y=2x+k的图象经过第一、三、四象限.
本题考查了一次函数图象:一次函数y=kx+b(k、b为常数,k≠0)是一条直线,当k>0,图象经过第一、三象限,y随x的增大而增大;当k<0,图象经过第二、四象限,y随x的增大而减小;图象与y轴的交点坐标为(0,b).
11.【答案】A
【解析】解:若设竿长AC为x尺,则BC为(x−4)尺,AB为(x−2)尺,
根据题意得:(x−4)2+(x−2)2=x2.
故选:A.
若设竿长AC为x尺,则BC为(x−4)尺,AB为(x−2)尺,利用勾股定理,可得出关于x的一元二次方程,此题得解.
本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
12.【答案】C
【解析】解:根据图2可知,
点P到B点时,y=PD−PB=0,
点P到C点时,y=PD−PB=3 2,
即AC=BD=3 2,
∴AB=AD=3.
点P到E点时,y= 32+(32)2−32=32 5−32,
点Q的横坐标为:3+32=92,
∴Q(92,32 5−32).
故选:C.
利用y=PD−PB开始为0,到最大值为3 2,也就是P到达B点时,即PD=3 2,PB=0,可求得对角线BD=3 2,从而求得边长AB=3,从而Q的横坐标为3+32=92,根据勾股定理可求出PD和PB的长,进而可得结论.
本题考查的是正方形中的动点问题,解题的关键是找到图中的关键点及对应的关键数.
13.【答案】x≥−2,且x≠1
【解析】解:由题可知,
x+2≥0,
即x≥−2,
又知分母不能等于0,
即x−1≠0,
则x≠1.
故答案为:x≥−2,且x≠1.
要使代数式有意义,则根式里面需要大于等于0,且分母不能为0.
本题考查二次根式有意义的条件,掌握二次根式有意义的条件是解题的关键.
14.【答案】1
【解析】解:∵四边形ABCD是菱形,
∴AC⊥BD,OD=12BD,OC=12AC,
∵AC=2 3,BD=2,
∴OD=1,OC= 3,
∴CD= OC2+OD2=2,
∵点E为边CD的中点,
∴OE=12CD=1.
故答案为:1.
由菱形的性质得到AC⊥BD,OD=12BD=1,OC=12AC= 3,由勾股定理求出CD= OC2+OD2=2,由直角三角形斜边中线的性质即可求出OE的长.
本题考查菱形的性质,直角三角形斜边的中线,勾股定理,关键是由菱形的性质,勾股定理求出CD的长,由直角三角形斜边中线的性质即可求出OE长.
15.【答案】1.5
【解析】解:根据题意得:130×(2.5×3+2×6+1.5×12+1×6+0.5×3)=1.5(h),
∴估计该校九年级学生每天完成作业的平均时长约是1.5h.
故答案为:1.5.
根据加权平均数的定义列式计算即可.
本题主要考查加权平均数,解题的关键是掌握加权平均数的定义.
16.【答案】m≥3
【解析】解:∵一次函数y=kx+b(k≠0)的图象由函数y=x的图象平移得到,
∴k=1,
将点(1,3)代入y=x+b,
得1+b=3,
解得b=2,
∴一次函数的解析式为y=x+2;
把点(1,3)代入y=mx,求得m=3,
∵当x>1时,对于x的每一个值,函数y=mx(m≠0)的值大于一次函数y=x+2的值,
∴m≥3.
故答案是:m≥3.
先根据直线平移时k的值不变得出k=1,再将点A(1,3)代入y=x+b,求出b的值,即可得到一次函数的解析式;根据点(1,3)和函数图象即可求得.
本题考查了一次函数图象与几何变换,一次函数与系数的关系,求直线平移后的解析式时要注意平移时k的值不变.
17.【答案】解:(1)原式=4÷2− 2−1
=2− 2−1
=1− 2;
(2)原式=4x2−5−4x2+8x
=8x−5,
当x= 3+1时,
原式=8 3+8−5
=8 3+3.
【解析】(1)先计算二次根式的除法和乘法以及零指数幂,再计算加减即可;
(2)原式先利用平方差公式和单项式乘多项式法则计算,再合并同类项即可化简,再将x的值代入即可求解.
此题考查了二次根式的化简求值和整式的混合运算-化简求值,熟练掌握各自的运算法则是解本题的关键.
18.【答案】6 7 7 甲
【解析】解:(1)把甲组的成绩从小到大排列后,中间两个数的平均数是6+62=6,则中位数a=6;b=110×(5+6+6+6+7+7+7+7+9+10)=7,
乙组学生成绩中,数据7出现了四次,次数最多,所以众数c=7.
故答案为:6;7;7;
(2)小明可能是甲组的学生,理由如下:
因为甲组的中位数是6分,而小明得了7分,所以在小组中属中游略偏上,
故答案为:甲;
(3)选乙组参加决赛.理由如下:S乙2=110[(5−7)2+(6−7)2+⋅⋅⋅+(10−7)2]=110(4+1+⋅⋅⋅+9)=110×20=2,
∵甲乙组学生平均数相等,而S甲2=3.76>S乙2=2,
∴乙组的成绩比较稳定,
故选乙组参加决赛.
(1)根据平均数、中位数和众数的定义分别进行解答即可得出答案;
(2)根据中位数的意义即可得出答案;
(3)根据平均数与方差的意义即可得出答案.
本题考查了平均数,中位数,众数,方差,正确理解它们的含义是解题关键.
19.【答案】 13 2 2
【解析】解:(1)由图可得,
AB= 32+22= 13,CD= 22+22=2 2,
故答案为: 13,2 2;
(2)以AB、CD、EF三条线段为边能构成直角三角形,
理由:∵AB= 13,CD=2 2,EF= 5,
∴CD2+EF2=(2 2)2+( 5)2=8+5=13=AB2,
∴以AB、CD、EF三条线段为边能构成直角三角形.
(1)根据勾股定理,可以求得AB和CD的长;
(2)根据勾股定理的逆定理可以判断以AB、CD、EF三条线段为边能否构成直角三角形.
本题考查勾股定理、勾股定理的逆定理,解答本题的关键是会用勾股定理的逆定理判断三角形的形状.
20.【答案】①
【解析】(1)证明:∵BE=FD,
∴BE+EF=FD+EF,
∴BF=DE,
∵AB//CD,
∴∠ABF=∠CDE,
在△ABF和△CDE中,
∠ABF=∠CDE∠BAF=∠DCEBF=DE,
∴△ABF≌△CDE(AAS);
(2)解:若选择条件①:
四边形AECF是菱形,理由如下:
由(1)得,△ABF≌△CDE,
∴AF=CE,∠AFB=∠CED,
∴AF//CE,
∴四边形AECF是平行四边形,
∵∠BAF=90∘,BE=EF,
∴AE=12BF,
∵∠BAF=90∘,∠ABD=30∘,
∴AF=12BF,
∴AE=AF,
∴▱AECF是菱形;
若选择条件②:
四边形AECF是菱形,理由如下:
连接AC交BD于点O,
由①得:△ABF≌△CDE,
∴AF=CE,∠AFB=∠CED,
∴AF//CE,
∴四边形AECF是平行四边形,
∴AO=CO,
∵AB=BC,
∴BO⊥AC,
即EF⊥AC,
∴▱AECF是菱形.
故答案为:①(答案不唯一).
(1)由等式的性质得BF=DE,由平行线的性质得∠ABF=∠CDE,从而利用AAS证明△ABF≌△CDE;
(2)若选择①,由(1)可说明AF//CE,则四边形AECF是平行四边形,由直角三角形斜边上中线的性质得AE=12BF,利用含30∘角的直角三角形的性质得AF=12BF,则AE=AF,从而▱AECF是菱形;若选择②连接AC交BD于点O,同理可得四边形AECF是平行四边形,利用等腰三角形的性质可得BO⊥AC,即EF⊥AC,从而证明结论.
主要考查了平行四边形的判定与性质,全等三角形的判定与性质,直角三角形斜边上中线的性质,等腰三角形的性质,菱形的判定等知识,熟练掌握菱形的判定定理是解题的关键.
21.【答案】解:(1)观察图象可知:x=7,y=2.75这组数据错误.
(2)设y=kx+b,把x=1,y=0.75,x=2,y=1代入可得k+b=0.752k+b=1,
解得k=14b=12,
∴y=14x+12,
当x=18时,y=5,
答:秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是5斤.
【解析】(1)利用描点法画出图形即可判断.
(2)设函数关系式为y=kx+b,利用待定系数法解决问题即可.
本题考查一次函数的应用,待定系数法等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
22.【答案】解:(1)四边形BFDE是菱形,理由如下:
根据作图可知:EF垂直平分BD,
∴BE=ED,BF=FD,
∵FE=EF,
∴△BFE≌△DFE,
∴∠BFE=∠DFE,
∵在ABCD中,AD//BC,
∴∠BFE=∠DEF,
∴∠DFE=∠DEF,
∴DE=DF,
∴BE=DE=DF=BF,
∴四边形BFDE是菱形;
(2)∵AB=4,AD=8,
∴AE=AD−BE=8−DE,
∵四边形BFDE是菱形,
∴BE=DE=DF=BF,
∴AE=8−DE=8−BE,
∵在Rt△ABE中,有AB2+AE2=BE2,
∴42+(8−BE)2=BE2,
∴BE=5,
∴DE=BE=5,
∴S菱形BEDF=DE×AB=5×4=20.
【解析】(1)根据作图可知:EF垂直平分BD,先证明△BFE≌△DFE,再证明∠DFE=∠DEF,即有DE=DF,进而有BE=DE=DF=BF,问题得解;
(2)由AD=8,可得AE=8−DE=8−BE,在Rt△ABE中,有AB2+AE2=BE2,即有42+(8−BE)2=BE2,解方程即可求出DE=BE=5,问题得解.
本题考查了垂直平分线的尺规作图,菱形的判定与性质,全等三角形的判定与性质以及勾股定理等知识,掌握菱形的判定与性质是解答本题的关键.
23.【答案】解:(1)设生产一件甲种产品需x分,生产一件乙种产品需y分.
由题意得:10x+10y=35030x+20y=850,
解这个方程组得:x=15y=20,
答:生产一件甲产品需要15分,生产一件乙产品需要20分;
(2)设生产甲种产品共用x分,则生产乙种产品用(25×8×60−x)分.
则生产甲种产品x15件,生产乙种产品25×8×60−x20件.
∴w总额=1.5×x15+2.8×25×8×60−x20
=0.1x+12000−x20×2.8
=0.1x+1680−0.14x
=−0.04x+1680,
又x15≥60,得x≥900,
由一次函数的增减性,当x=900时w取得最大值,此时w=−0.04×900+1680=1644(元),
则小王该月收入最多是1644+1900=3544(元),
此时甲有90015=60(件),
乙有:25×8×60−90020=555(件),
答:小王该月最多能得3544元,此时生产甲、乙两种产品分别60,555件.
【解析】本题考查了一次函数和二元一次方程组的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.
(1)设生产一件甲种产品需x分,生产一件乙种产品需y分,利用待定系数法求出x,y的值.
(2)设生产甲种产品用x分,则生产乙种产品用(25×8×60−x)分,分别求出甲乙两种生产多少件产品.
24.【答案】n>1
【解析】解:(1)把C(1,m)代入l1:y=x+3得:m=1+3=4,
∴点C的坐标为(1,4),
设直线l2的解析式为y=kx+b(k≠0),把A(3,0),C(1,4)代入得:
3k+b=0k+b=4,
解得:k=−2b=6,
∴直线l2的解析式为y=−2x+6.
(2)①根据函数图象可知,当点M、N在点C右边时,点M位于点N上方,
∴n>1,
故答案为:n>1;
②把y=0代入y=x+3得:x+3=0,解得:x=−3,
∴B(−3,0),
∴AB=3−(−3)=6,
把x=n分别代入y=x+3和y=−2x+6得M(n,n+3),N(n,−2n+6),
∵MN=AB,点M位于点N上方,
∴n+3−(−2n+6)=6,
解得:n=3,
∴此时点M的坐标为:(3,6).
(1)先求出点C的坐标,然后根据待定系数法求出一次函数解析式即可;
(2)①根据当点M、N在点C右边时,点M位于点N上方,写出n的取值范围即可;
②先求出点B的坐标,用n表示出点M、N的坐标,然后根据MN=AB列出关于n的方程,解方程得出n的值,即可得出答案.
本题主要考查了求一次函数解析式,两条直线的交点问题,解题的关键是熟练掌握待定系数法求一次函数解析式,数形结合,准确计算.
25.【答案】∠BME或∠ABP或∠PBM或∠MBC15∘
【解析】解:(1)∵AE=BE=12AB,AB=BM,
∴BE=12BM,
∵∠BEM=90∘,
∴∠BME=30∘,
∴∠MBE=60∘,
∵∠ABP=∠PBM,
∴∠ABP=∠PBM=∠MBC=30∘;
故答案为:∠BME或∠ABP或∠PBM或∠MBC;
(2)①∵四边形ABCD是正方形,
∴AB=BC,∠A=∠ABC=∠C=90∘,
由折叠性质得:AB=BM,∠PMB=∠BMQ=∠A=90∘,
∴BM=BC;
∵BQ=BQ,
∴Rt△BQM≌Rt△BQC(HL),
∴∠MBQ=∠CBQ,
∵∠MBC=30∘,
∴∠MBQ=∠CBQ=15∘;
故答案为:15∘;
②∠MBQ=∠CBQ,理由如下:
∵BM=BC,BQ=BQ,
∴Rt△BQM≌Rt△BQC(HL),
∴∠MBQ=∠CBQ;
(3)当点Q在点F的下方时,如图,
∵FQ=1cm,DF=FC=4cm,AB=8cm,
∴QC=CD−DF−FQ=8−4−1=3(cm),DQ=DF+FQ=4+1=5(cm),
由(2)可得,QM=QC=3(cm),
设AP=PM=xcm,PD=(8−x)cm,
∵PD2+DQ2=PQ2,
即(8−x)2+52=(x+3)2,
解得:x=4011,
∴AP=4011(cm);
当点Q在点F的上方时,如图,
∵FQ=1cm,DF=FC=4cm,AB=8cm,
∴QC=5cm,DQ=3cm,
由(2)可知,QM=QC=5cm,
设AP=PM=xcm,PD=(8−x)cm,
∴PD2+DQ2=PQ2,
即(8−x)2+32=(x+5)2,
解得:x=2413,
∴AP=2413cm.
综上所述:AP为4011cm或2413cm.
(1)根据折叠的性质,得BE=12BM,结合矩形的性质得∠BME=30∘,进而可得∠ABP=∠PBM=∠MBC=30∘;
(2)①根据折叠的性质,可证Rt△BQM≌Rt△BQC(HL),即可求解,
②根据折叠的性质,可证Rt△BQM≌Rt△BQC(HL),即可求解;
(3)由(2)可得QM=QC,分两种情况:当点Q在点F的下方时,当点Q在点F的上方时,设AP=PM=xcm,分别表示出PD,DQ,PQ,由勾股定理即可求解.
本题主要考查矩形与折叠,正方形的性质、勾股定理、三角形的全等,掌握相关知识并灵活应用是解题的关键.时长/h
2.5
2
1.5
1
0.5
人数
3
6
12
6
3
组别
平均数
中位数
众数
方差
甲组
7
a
6
3.76
乙组
b
7
c
S乙2
x(厘米)
1
2
4
7
11
12
y(斤)
0.75
1.00
1.50
2.75
3.25
3.50
生产甲产品数(件)
生产乙产品数(件)
所用时间(分钟)
10
10
350
30
20
850
2023-2024学年贵州省黔东南州七年级(下)期末数学试卷(含详细答案解析): 这是一份2023-2024学年贵州省黔东南州七年级(下)期末数学试卷(含详细答案解析),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年贵州省安顺市七年级(下)期末数学试卷(含详细答案解析): 这是一份2023-2024学年贵州省安顺市七年级(下)期末数学试卷(含详细答案解析),共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年贵州省三联教育集团七年级(下)期末数学试卷(含详细答案解析): 这是一份2023-2024学年贵州省三联教育集团七年级(下)期末数学试卷(含详细答案解析),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












