

2023-2024学年贵州省铜仁市八年级(下)期末数学模拟试卷(含详细答案解析)
展开1.下列选项中,属于最简二次根式的是( )
A. 5B. 12C. 0.7D. 8
2.对于任意的正数x、y的新定义运算⊗为:x⊗y x− y(x≥y) x+ y(x
3.为了丰富学生的课余生活,某班级举行趣味运动会,其中一项是飞镖,记录小江同学的成绩获得5个数据(单位:环),并进行整理、分析,得到这组数据的四个统计量如下表:
则小江的5次飞镖成绩可能是( )
A. 5,7,8,8,10B. 5,6,7,8,8C. 6,7,8,8,9D. 6,7,7,8,10
4.已知△ABC的三边分别为a,b,c,则下列条件中不能判定△ABC是直角三角形的是( )
A. ∠A:∠B;∠C=3:4:5B. b2=a2−c2
C. a:b:c=1: 3:2D. ∠A=∠B−∠C
5.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b.若大正方形的面积为16,小正方形的面积是3,则(a+b)2是( )
A. 19B. 13C. 42D. 29
6.如图所示,Rt△ABC中,∠C=90∘,BC=6,AC=8,D、E分别为AC、BC的中点,连接DE,则DE长为( )
A. 4
B. 5
C. 6
D. 7
7.如图,在菱形ABCD中,∠ABC=140∘,则∠DAC等于( )
A. 30∘
B. 25∘
C. 20∘
D. 15∘
8.如图,四边形ABCD的对角线AC,BD相交于点O,OA=OC,AD//BC,则下列说法错误的是( )
A. 若AC=BD,则四边形ABCD是矩形
B. 若BD平分∠ABC,则四边形ABCD是菱形
C. 若AB⊥BC且AC⊥BD,则四边形ABCD是正方形
D. 若AB=BC且AC⊥BD,则四边形ABCD是正方形
9.如图,正方形ABCD中,点E在对角线AC上,连接EB、ED,延长BE交AD于点F,若∠DEB=α,则∠AFE的度数为( )
A. 135∘−α2
B. 135∘+α2
C. 90∘−α2
D. 90∘+a2
10.甲、乙、丙、丁四名同学参加立定跳远训练,他们成绩的平均数相同,方差如下:s甲2=1.1,s乙2=2.2,s丙2=0.5,s丁2=0.8,则成绩最稳定的是( )
A. 甲B. 乙C. 丙D. 丁
11.一次函数y=kx+b的图象与正比例函数y=−5x的图象平行且经过点A(2,−3),则kb等于( )
A. 0B. −35C. 35D. −12
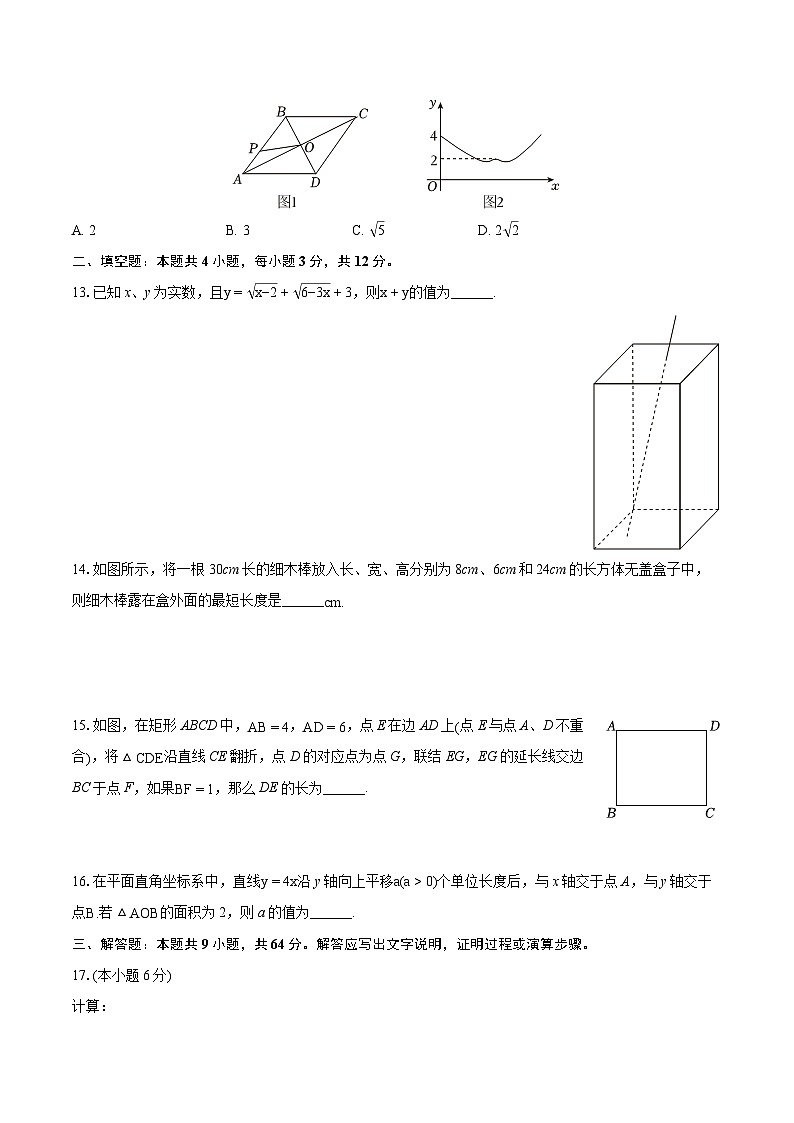
12.如图1,动点P从菱形ABCD的点A出发,沿边AB→BC匀速运动,运动到点C时停止.设点P的运动路程为x,PO的长为y,y与x的函数图象如图2所示,当点P运动到BC中点时,PO的长为( )
A. 2B. 3C. 5D. 2 2
二、填空题:本题共4小题,每小题3分,共12分。
13.已知x、y为实数,且y= x−2+ 6−3x+3,则x+y的值为______.
14.如图所示,将一根30cm长的细木棒放入长、宽、高分别为8cm、6cm和24cm的长方体无盖盒子中,则细木棒露在盒外面的最短长度是______cm.
15.如图,在矩形ABCD中,AB=4,AD=6,点E在边AD上(点E与点A、D不重合),将△CDE沿直线CE翻折,点D的对应点为点G,联结EG,EG的延长线交边BC于点F,如果BF=1,那么DE的长为______.
16.在平面直角坐标系中,直线y=4x沿y轴向上平移a(a>0)个单位长度后,与x轴交于点A,与y轴交于点B.若△AOB的面积为2,则a的值为______.
三、解答题:本题共9小题,共64分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题6分)
计算:
(1) 48÷ 3− 15× 30+ 24;
(2)( 3−1)2−(3+ 5)(3− 5).
18.(本小题6分)
如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时梯子底部B到墙底端的距离为0.7米,考虑爬梯子的稳定性,现要将梯子顶部A沿墙下移0.4米到A′处,问梯子底部B将外移多少米?
19.(本小题6分)
如图,在正方形ABCD中,点E在边CD上(与C、D均不重合).
(1)尺规作图:过点C作BE的垂线CF,垂足为点H,交AD于点F(要求:保留作图痕迹,不写作法);
(2)在(1)所作的图形中,已知BC=4,CE=3,求CH的长度.
20.(本小题6分)
如图,平行四边形ABCD的对角线AC、BD相交于点O,E、F分别是OA、OC的中点,求证:BE=DF.
21.(本小题7分)
如图,四边形ABCD的对角线AC与BD相交于点O,AD//BC,∠ABC=90∘,有下列条件:
①AB//CD,②AD=BC.
(1)请从以上①②中任选1个作为条件,求证:四边形ABCD是矩形;
(2)在(1)的条件下,若AB=3,AC=5,求四边形ABCD的面积.
22.(本小题7分)
为了解某校八年级学生每周参加科学教育的时间(单位:h),随机调查了该校八年级a名学生,根据统计的结果,绘制出如图的统计图①和图②.
请根据相关信息,解答下列问题:
(Ⅰ)填空:a的值为______,图①中 m的值为______,统计的这组学生每周参加科学教育的时间数据的众数和中位数分别为______和______;
(Ⅱ)求统计的这组学生每周参加科学教育的时间数据的平均数;
(Ⅲ)根据样本数据,若该校八年级共有学生500人,估计该校八年级学生每周参加科学教育的时间是9h的人数约为多少?
23.(本小题8分)
在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y=−kx+3的图象交于点(2,1).
(1)求k,b的值;
(2)当x>2时,对于x的每一个值,函数y=mx(m≠0)的值既大于函数y=kx+b的值,也大于函数y=−kx+3的值,直接写出m的取值范围.
24.(本小题8分)
A,B,C三地在同一条公路上,C地在A,B两地之间,且到A,B两地的路程相等.甲、乙两车分别从A,B两地出发,匀速行驶.甲车到达C地并停留1小时后以原速继续前往B地,到达B地后立即调头(调头时间忽略不计),并按原路原速返回C地停止行驶,乙车经C地到达A地停止行驶.在两车行驶的过程中,甲、乙两车距C地的路程y(单位:千米)与所用的时间x(单位:小时)之间的函数图象如图所示,请结合图象信息解答下列问题:
(1)直接写出A,B两地的路程和甲车的速度;
(2)求乙车从C地到A地的过程中y与x的函数关系式(不用写自变量的取值范围).
25.(本小题10分)
(1)【探究】如图1,正方形ABCD中,点E、F分别是BC,CD上一点,∠EAF=45∘.
①求证:BE+DF=EF;
②若BE=3,CF=4,求正方形的边长AB.
(2)【应用】如图2,正方形ABCD中,点E在AB边上(不与端点重合),F、G分别是CD,BC上一点,EF交AG于点M,∠FMG=45∘,若GC=2BG,直接写出EFAG的值.
答案和解析
1.【答案】A
【解析】解:A. 5的被开方数是整数,且不含有能开得尽方的因数,因此 5是最简二次根式,所以选项A符合题意;
B. 12= 22,因此 12不是最简二次根式,所以选项B不符合题意;
C. 0.7= 710= 7010,因此 0.7不是最简二次根式,所以选项C不符合题意;
D. 8=2 2,因此 8不是最简二次根式,所以选项D不符合题意.
故选:A.
根据最简二次根式的定义,即“被开方数是整数或整式,且不含有能开得尽方的因数或因式的二次根式是最简二次根式”,逐个进行判断即可.
本题考查最简二次根式,掌握“被开方数是整数或整式,且不含有能开得尽方的因数或因式的二次根式是最简二次根式”是正确解答的关键.
2.【答案】D
【解析】解:(18⊗12)+(27⊗32)
= 18− 12+ 27+ 32
=3 2−2 3+3 3+4 2
=7 2+ 3.
故选:D.
先根据新定义运算,将原式转化成二次根式加减运算,再根据二次根式加减运算法则计算即可.
本题考查了实数的运算,掌握实数的运算法则是解题的关键.
3.【答案】C
【解析】解:A、B、C的众数为8,D的众数为7,排除D选项;
A、C的中位数为8,B的中位数为7,排除B选项;
平均数xA=5+7+8+8+105=7.6,xC=6+7+8+8+95=7.6均满足题意;
方差A=15[(5−7.6)2+(7−7.6)2+2(8−7.6)2+(10−7.6)2]=2.608不符合题意;方差C=[(6−7.6)2+(7−7.6)2+2(8−7.6)2+(9−7.6)2]=1.04符合题意.
故选:C.
根据众数的定义可排除D选项,根据中位数的定义可排除B选项,根据方差的定义即可解答.
本题主要考查了众数、中位数、平均数、方差的求法,掌握它们的计算方法成为解题的关键.
4.【答案】A
【解析】解:A、设∠A=3x∘,∠B=4x∘,∠C=5x∘,
3x+4x+5x=180,
解得:x=15,
则5x∘=75∘,
∴△ABC不是直角三角形,故此选项符合题意;
B、∵b2=a2−c2,
∴能构成直角三角形,故此选项不符合题意;
C、∵( 3)2+12=22,
∴能构成直角三角形,故此选项不合题意;
D、∵∠A=∠B−∠C,∠A+∠B+∠C=180∘,
∴∠B=90∘,
∴△ABC为直角三角形,故此选项不合题意;
故选:A.
根据三角形内角和定理可分析出A、C的正误;根据勾股定理逆定理可分析出B、D的正误.
本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.
5.【答案】D
【解析】解:∵设直角三角形较长直角边长为a,较短直角边长为b,
∴S直角三角形=12ab,且直角三角形的斜边长为 a2+b2,
∴大正方形的边长为 a2+b2,则S大正方形=( a2+b2)2=a2+b2=16,
∵大正方形的面积为16,小正方形的面积是3,
∴S大正方形=S小正方形+4S直角三角形,即16=3+4×12ab,则2ab=13,
∴(a+b)2=a2+b2+2ab=16+13=29,
故选:D.
根据题意,求出大正方形边长、直角三角形面积、大正方形面积,进而得到a2+b2=16,2ab=13,利用完全平方和公式展开后,代入求值即可得到答案.
本题考查“赵爽弦图”为背景的代数式求值,涉及勾股定理、三角形面积及正方形面积等知识,熟练掌握“赵爽弦图”图形构成,数形结合,掌握代数式求值方法是解决问题的关键.
6.【答案】B
【解析】解:∵Rt△ABC中,∠C=90∘,BC=6,AC=8,
∴AB= BC2+AC2=10,
∵D、E分别为AC、BC的中点,
∴DE=12AB=5.
故选:B.
先根据勾股定理可得AB=10,然后根据三角形中位线等于底边的一半即可解答.
本题主要考查了勾股定理、三角形中位线的性质等知识点,掌握三角形中位线等于底边的一半成为解题的关键.
7.【答案】C
【解析】解:∵四边形ABCD是菱形,∠ABC=140∘,
∴∠DAB=180∘−140∘=40∘,
∴∠DAC=12∠DAB=20∘,
故选:C.
根据菱形的邻角互补和对角线平分对角解答即可.
此题考查菱形的性质,关键是根据菱形的邻角互补得出∠DAB解答.
8.【答案】D
【解析】解:∵AD//BC,
∴∠ADO=∠CBO,
∵OA=OC,∠AOD=∠BOC,
在△AOD和△COB中,
∠ADO=∠CBO∠AOD=∠BOCAO=OC,
∴△AOD≌△COB(AAS),
∴AD=BC,
∵AD//BC,
∴四边形ABCD是平行四边形,
若AC=BD,则四边形ABCD是矩形,故A选项不符合题意;
若BD平分∠ABC,
∴∠ABD=∠ADB,
∴AB=AD,
则四边形ABCD是菱形,故B选项不符合题意;
若AB⊥BC且AC⊥BD,则四边形ABCD是正方形,故C选项不符合题意;
若AB=BC且AC⊥BD,则四边形ABCD是菱形,故D选项符合题意;
故选:D.
先根据平行四边形的判定证明ABCD是平行四边形,再根据已知条件结合菱形、矩形及正方形的判定逐一判断即可.
本题考查平行四边形的判定、菱形的判定与矩形的判定、正方形的判定,熟练掌握相关定理是解题的关键.
9.【答案】A
【解析】解:∵四边形ABCD是正方形,
∴CD=CB,∠ACD=∠ACB=∠DAC=45∘,
在△DCE和△BCE中,
CD=CB∠ECD=∠ECBCE=CE,
∴△DCE≌△BCE(SAS),
∴∠DEC=∠BEC,
∵∠DEB=α,
∴∠BEC=α2,
∴∠AEF=∠BEC=α2,
∴∠AFE=180∘−∠AEF−∠DAC=180∘−α2−45∘=135∘−α2,
故选:A.
根据正方形的性质可证得△DCE和△BCE全等,即可求出∠BEC的度数,再根据三角形内角和定理即可求出∠AFE的度数.
本题考查了正方形的性质,全等三角形的判定与性质,三角形内角和定理,熟练掌握正方形的性质及三角形的判定定理是解题的关键.
10.【答案】C
【解析】解:因为s甲2=1.1,s乙2=2.2,s丙2=0.5,s丁2=0.8,
所以S丙2
故选:C.
直接根据方差的意义进行判断.
本题考查了方差:方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,稳定性越好.
11.【答案】B
【解析】解:∵一次函数y=kx+b的图象与正比例函数y=−5x的图象平行,
∴k=−5,
∴y=−5x+b,
把A(2,−3)代入得−10+b=−3,
解得b=7,
∴kb=−5×7=−35.
故选:B.
根据两直线平行的问题得到k=−5,再把A点坐标代入y=−5x+b中计算出k的值,然后计算kb.
本题考查了两直线平行或相交的问题:直线y=k1x+b1(k1≠0)和直线y=k2x+b2(k2≠0)平行,则k1=k2;若直线y=k1x+b1(k1≠0)和直线y=k2x+b2(k2≠0)相交,则交点坐标满足两函数的解析式.
12.【答案】C
【解析】解:结合图象,得到当x=0时,PO=AO=4,
∴当点P运动到点B时,PO=BO=2,
∵菱形ABCD,
∴AC⊥BD,
∴∠AOB=∠BOC=90∘,
∴AB=BC= OA2+OB2=2 5,
当点P运动到BC中点时,PO的长为12BC= 5,
故选:C.
结合图象,得到当x=0时,PO=AO=4,当点P运动到点B时,PO=BO=2,根据菱形的性质,得∠AOB=∠BOC=90∘,继而得到AB=BC= OA2+OB2=2 5,当点P运动到BC中点时,PO的长为12BC= 5,解得即可.
本题考查了菱形的性质,勾股定理,直角三角形的性质,熟练掌握菱形的性质,勾股定理,直角三角形的性质是解题的关键.
13.【答案】5
【解析】解:∵y= x−2+ 6−3x+3,
∴x−2≥06−3x≥0,
∴x=2,
∴y=3,
∴x+y=5,
故答案为:5.
直接利用二次根式有意义的条件得出x的值,进而得出y的值,进而得出答案.
此题主要考查了二次根式有意义的条件,掌握二次根式被开方数不小于零的条件是解题的关键.
14.【答案】4
【解析】解:由题可知,盒子底面对角线长为 62+82=10(cm),
盒子的对角线长: 102+242=26(cm),
∵细木棒长30cm,
故细木棒露在盒外面的最短长度是:30−26=4(cm),
故答案为:4.
长方体内体对角线是最长的,当木条在盒子里对角放置的时候露在外面的长度最小,利用勾股定理计算即可.
本题主要考查了勾股定理的应用,解题的关键是熟练掌握勾股定理.
15.【答案】2
【解析】解:如图所示,CD=AB=4,
由折叠可得,D,G关于CE对称,
∴CE垂直平分DG,
∴∠CDG+∠DCE=90∘,
∵∠ADC=90∘,
∴∠CDG+∠ADF=90∘,
∴∠DCE=∠ADF,
又∵∠A=∠CDE=90∘,
∴△ADF∽△DCE,
∴DEAF=DCAD,即DE4−1=46,
解得DE=2.
故答案为:2.
依据∠DCE=∠ADF,∠A=∠CDE=90∘,即可判定△ADF∽△DCE;再根据相似三角形的对应边成比例,即可得到DE的长.
本题主要考查了相似三角形的判定与性质,解决问题的关键是利用相似三角形的对应边成比例.
16.【答案】4
【解析】解:直线y=4x沿y轴向上平移a个单位长度后,得到直线y=4x+a,
当y=0时,0=4x+a,
∴x=−a4,
∵直线y=4x+a与x轴交于点A,
∴OA=|−a4|=a4,
当x=0时,y=a,
∴OB=a,
∵△AOB的面积为2,
∴12×a4×a=2,
∴a=4(负值舍去).
故答案为:4.
利用平移的规律求得平移后的直线解析式,然后分别计算x=0和y=0时对应的值,可得OA和OB的值,根据△AOB的面积为2,列方程可得结论.
本题考查了一次函数的平移,一次函数上点的坐标特征,三角形的面积,计算OA和OB的长是解本题的关键.
17.【答案】解:(1)原式= 16− 6+2 6
=4+ 6;
(2)原式=3−2 3+1−(9−5)
=−2 3.
【解析】(1)先算乘除,再算加减即可;
(2)先利用平方差公式和完全平方公式展开,再计算即可.
本题考查二次根式的混合运算,正确进行计算是解题关键.
18.【答案】解:在Rt△ABC中,∵AB=2.5米,BC=0.7米,
∴AC= AB2−BC2= 2.52−0.72=2.4(米),
又∵AA′=0.4米,
∴A′C=2.4−0.4=2(米),
在Rt△A′B′C中,B′C= A′B′2−A′C2= 2.52−22=1.5(米),
则BB′=CB′−CB=1.5−0.7=0.8(米).
故:梯子底部B外移0.8米.
【解析】在Rt△ABC中,根据已知条件运用勾股定理可将AC的长求出,又知AA′的长可得AC的长,在Rt△A′B′C中再次运用勾股定理可将B′C求出,B′C的长减去BC的长即为底部B外移的距离.
本题考查正确运用勾股定理,比较简单.
19.【答案】解:(1)图形如图所示:
(2)∵四边形ABCD是正方形,
∴∠BCE=90∘,
∵BC=4,CE=3,
∴BE= BC2+CE2= 42+32=5,
∵CH⊥BE,
∴S△BCE=12⋅BC⋅EC=12⋅BE⋅CH,
∴CH=3×45=125.
【解析】(1)根据要求作出图形;
(2)利用勾股定理求出BE,再利用面积法求出CH.
本题考查作图-复杂作图,正方形的性质,勾股定理,三角形的面积等知识,解题的关键是熟练掌握五种基本作图,属于中考常考题型.
20.【答案】证明:连接BF、DE,如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E、F分别是OA、OC的中点,
∴OE=12OA,OF=12OC,
∴OE=OF,
∴四边形BFDE是平行四边形,
∴BE=DF.
【解析】本题考查了平行四边形的基本性质和判定定理的运用.根据平行四边形的性质:对角线互相平分得出OA=OC,OB=OD,利用中点的意义得出OE=OF,从而利用平行四边形的判定定理“对角线互相平分的四边形是平行四边形”判定四边形BFDE是平行四边形,从而得出BE=DF.
21.【答案】(1)选择①,证明:∵AD//BC,AB//CD,
∴四边形ABCD是平行四边形,
∵∠ABC=90∘,
∴四边形ABCD是矩形;
选择②,证明:∵AD//BC,AD=BC,
∴四边形ABCD是平行四边形,
∵∠ABC=90∘,
∴四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,
∴∠ABC=90∘,
∵AB=3,AC=5,
∴BC= AC2−AB2=4,
∴四边形ABCD的面积=AB⋅BC=3×4=12.
【解析】(1)根据矩形的判定定理即可得到结论;
(2)根据矩形 到现在得到∠ABC=90∘,根据勾股定理得到BC= AC2−AB2=4,根据矩形的面积公式得到四边形ABCD的面积=AB⋅BC=3×4=12.
本题考查了矩形的判定和性质,平行四边形的判定和性质,勾股定理,熟练掌握矩形的判定和性质定理是解题的关键.
22.【答案】50 34 8 8
【解析】解:(I)a=3+7+17+15+8=50(人);
m%=1750=34%;
3+7+17=27(人),中位数位于8h这组;
众数是8h;
故答案为:50,34,8,8.
(II)观察条形统计图,
∵6×3+7×7+17×8+15×9+8×1050=8.36(h),
∴这组数据的平均数是8.36.
(III)∵在所抽取的样本中,每周参加科学教育的时间是9h的学生占30%,
∴根据样本数据,估计该校八年级学生500人中,每周参加科学教育的时间是9h的学生占30%,有500×30%=150(人),
∴估计该校八年级学生每周参加科学教育的时间是9h的人数约为150人.
(I)a=3+7+17+15+8=50(人);m%=1750=34%;根据中位数和众数的定义即可得出结果;
(II)根据条形统计图,可知平均数6×3+7×7+17×8+15×9+8×1050,计算即可;
(III)用样本估计总体,可知估计该校八年级学生500人中,每周参加科学教育的时间是9h的学生占30%,有500×30%,计算即可.
本题考查的是条形统计图,用样本估计总体,加权平均数,中位数,众数,正确掌握上述知识点是解题的关键.
23.【答案】解:(1)∵直线y=−kx+3点(2,1),
∴−2k+3=1,
解得k=1,
将点(2,1)代入y=x+b得:2+b=1,
解得b=−1.
(2)∵当x>2时,对于x的每一个值,函数y=mx(m≠0)的值既大于函数y=x−1的值,也大于函数y=−x+3的值,
∴m≥1.
∴m的取值范围是m≥1.
【解析】(1)先根据直线y=−kx+3点(2,1)得出k=1,再将点(2,1)代入y=x+b,求出b的值;
(2)根据图象即可求得.
本题是两条直线相交或平行问题,考查了待定系数法求一次函数的解析式,一次函数与系数的关系,数形结合是解题的关键.
24.【答案】解:(1)∵AC=BC=180,
∴AB=360,
∴A,B两地的路程是360千米;
甲车的速度是180×3÷(5.5−1)=120(千米/小时).
(2)∵A地到C地与C地到B地路程相等,且匀速行驶,
∴乙车从B地到C地与从C地到A地所用时间相等,均为6÷2=3(小时).
设乙车从C地到A地的过程中y与x的函数关系式为y=kx+b(k、b为常数,且k≠0).
将坐标(3,0)和(6,180)分别代入y=kx+b,
得3k+b=06k+b=180,
解得k=60b=−180,
∴乙车从C地到A地的过程中y与x的函数关系式为y=60x−180.
【解析】(1)由ABC三地之间的路程关系求得A,B两地的路程,根据“甲车的速度=甲车从出发到停止行驶的路程÷行驶的时间”求出甲车的速度即可;
(2)A地到C地与C地到B地路程相等,且匀速行驶,故乙车从B地到C地与从C地到A地所用时间相等,从而求得乙车从B地到达C地所用的时间,再利用待定系数法求函数关系式即可.
本题考查一次函数的应用,掌握速度、时间、路程之间的关系及待定系数法求函数关系式是解题的关键.
25.【答案】(1)①证明:延长CB至点Q,使得BQ=DF,连接AQ,EF,如图1,
∵四边形ABCD是正方形,
∴AD=AB,∠ABQ=∠D=90∘,
∵BQ=DF,
∴△QAB≌△FAD(SAS),
∴∠QAB=∠DAF,QA=AF,
∵∠EAF=45∘,∠BAD=90∘,
∴∠QAB+∠BAE=∠DAF+∠BAE=45∘,
∴∠QAE=∠FAE,
∵AE=AE,
∴△QAE≌△FAE(SAS),
∴QE=EF,
∴EF=BE+BQ=BE+DF;
②解:设正方形边长为x,
∵BE=3,CF=4,
∴CE=x−3,DF=x−4,
由①得EF=BE+DF=x−1,
根据勾股定理得(x−3)2+42=(x−1)2,
解得x=6,
正方形的边长AB=6.
(2)解:作AN//EF,连接GN,如图2,
设正方形的边长为6a,DN=m,
∴∠FMG=∠NAG=45∘,四边形AEFN是平行四边形,
∴EF=AN,
∵GC=2BG,
∴GC=2BG=4a,CN=6a−m,GN=2a+m,
根据勾股定理得,(4a)2+(6a−m)2=(2a+m)2,
解得m=3a,
则AN= DN2+AD2=3 5a,AG= BG2+AB2=2 10a,
∴EFAG=ANAG=3 5a2 10a=3 24.
【解析】(1)①延长CB至点Q,使得BQ=DF,连接AQ,EF,先证明△QAB≌△FAD,再证明△QAE≌△FAE,得到QE=EF,
进而推导出EF=BE+BQ=BE+DF;
②设正方形边长为x,根据①中结论列方程求解即可;
(2)作AN//EF,连接GN,设正方形的边长为6a,DN=m,推导出∠FMG=∠NAG=45∘,四边形AEFN是平行四边形,
进而得到EF=AN,GC=2BG=4a,CN=6a−m,GN=2a+m,根据勾股定理得(4a)2+(6a−m)2=(2a+m)2,解得m=3a,进而得到则AN=3 5a,AG=2 10a,EFAG=3 24.
本题考查了正方形的性质,全等三角形的判定与性质,平行四边形的判定和性质,勾股定理,解题关键是根据正方形的性质证明三角形全等,利用勾股定理求出线段长.姓名
平均数(环)
众数(环)
中位数(环)
方差S2(环 2)
小江
7.6
8
8
S2<2
2023-2024学年贵州省黔南州八年级(下)期末数学试卷(含详细答案解析): 这是一份2023-2024学年贵州省黔南州八年级(下)期末数学试卷(含详细答案解析),共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年贵州省遵义市八年级(下)期末数学试卷(含详细答案解析): 这是一份2023-2024学年贵州省遵义市八年级(下)期末数学试卷(含详细答案解析),共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年贵州省安顺市八年级(下)期末数学试卷(含详细答案解析): 这是一份2023-2024学年贵州省安顺市八年级(下)期末数学试卷(含详细答案解析),共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












