迪庆市重点中学2023-2024学年数学八年级第一学期期末联考模拟试题【含解析】

这是一份迪庆市重点中学2023-2024学年数学八年级第一学期期末联考模拟试题【含解析】，共22页。试卷主要包含了如图，是线段上的两点，，如图，直线与的图像交于点，若分式方程有增根， 则的值是等内容，欢迎下载使用。
注意事项：
1． 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。
2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。
3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。
4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1．一项工程，一半由甲单独做需要m小时完成，另一半由乙单独做需要n小时完成，则甲、乙合做这项工程所需的时间为（ ）
A．小时B．小时C．小时D．小时
2．如图，，要说明，需添加的条件不能是（ ）
A．B．C．D．
3．已知图中的两个三角形全等，则等于( )
A．B．C．D．
4．在平面直角坐标系中，如果点A的坐标为(﹣1，3)，那么点A一定在( )
A．第一象限B．第二象限C．第三象限D．第四象限
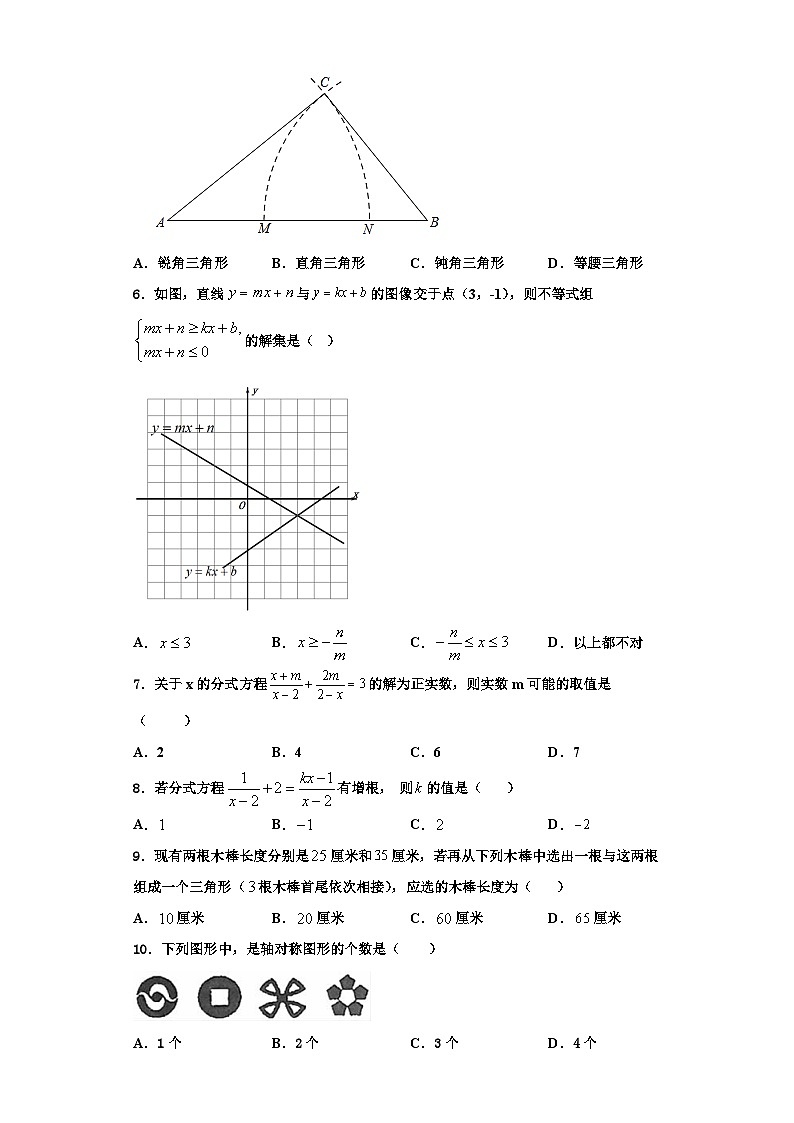
5．如图，是线段上的两点，．以点为圆心，长为半径画弧；再以点为圆心，长为半径画弧，两弧交于点，连结，则一定是（ ）
A．锐角三角形B．直角三角形C．钝角三角形D．等腰三角形
6．如图，直线与的图像交于点（3，-1），则不等式组的解集是（ ）
A．B．C．D．以上都不对
7．关于x的分式方程的解为正实数，则实数m可能的取值是（ ）
A．2B．4C．6D．7
8．若分式方程有增根， 则的值是（ ）
A．B．C．D．
9．现有两根木棒长度分别是厘米和厘米，若再从下列木棒中选出一根与这两根组成一个三角形（根木棒首尾依次相接），应选的木棒长度为（ ）
A．厘米B．厘米C．厘米D．厘米
10．下列图形中，是轴对称图形的个数是（ ）
A．1个B．2个C．3个D．4个
二、填空题(每小题3分,共24分)
11．三角形三条中线交于一点，这个点叫做三角形的_____．
12．已知是关于的二元一次方程的一个解，则的值为_____．
13．如图，我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形，若小正方形与大正方形的面积之比为1：13，则直角三角形较短的直角边a与较长的直角边b的比值为 ．
14．某鞋店一周内销售了某种品牌的男鞋双，各种尺码的销售量统计如下：
由此你能给这家鞋店提供的进货建议是________________________.
15．如图，点P是∠BAC的平分线AD上一点，PE⊥AC于点E．已知PE=3，则点P到AB的距离是_____
16．一根木棒能与长为和的两根木棒钉成一个三角形，则这根木棒的长度的取值范围是____________．
17．如图，中，，，，平分，为的中点．若，，则__________．（用含，的式子表示）
18．已知一次函数y=-x+3，当0≤x≤2时，y的最大值是 ．
三、解答题(共66分)
19．（10分）某小区积极创建环保示范社区，决定在小区内安装垃圾分类的温馨提示牌和垃圾箱，已知温馨提示牌的单价为每个30元，垃圾箱的单价为每个90元，共需购买温馨提示牌和垃圾箱共100个.
（1）若规定温馨提示牌和垃圾箱的个数之比为1:4，求所需的购买费用；
（2）若该小区至多安放48个温馨提示牌，且费用不超过6300元，请列举所有购买方案，并说明理由.
20．（6分）如图，点、在上，，，.
求证：.
21．（6分）如图，在中，于点E，BC的垂直平分线分别交AB、BE于点D、G，垂足为H，，CD交BE于点F
求证：≌
若，求证：
平分
．
22．（8分）如图，是等边三角形，为上两点，且，延长至点，使，连接．
（1）如图1，当两点重合时，求证：；
（2）延长与交于点．
①如图2，求证：；
②如图3，连接，若，则的面积为______________．
23．（8分）今年清明节前后某茶叶销售商在青山茶厂先后购进两批茶叶．第一批茶叶进货用了5.4万元，进货单价为a元/千克．购回后该销售商将茶叶分类包装出售，把其中300千克精装品以进货单件的两倍出售；余下的简装品以150元/千克的价格出售，全部卖出．第二批进货用了5万元，这一次的进货单价每千克比第一批少了20元．购回分类包装后精装品占总质量的一半，以200元/千克的单价出售；余下的简装品在这批进货单价的基础上每千克加价40元后全部卖出．若其它成本不计，第二批茶叶获得的毛利润是3.5万元．
（1）用含a的代数式表示第一批茶叶的毛利润；
（2）求第一批茶叶中精装品每千克售价．（总售价-总进价=毛利润）
24．（8分）如图，在平面直角坐标系中，等腰直角三角形ABC的顶点A在x轴上，AB＝AC，∠BAC＝90°，且A（2，0）、B（3，3），BC交y轴于M，
（1）求点C的坐标；
（2）连接AM，求△AMB的面积；
（3）在x轴上有一动点P，当PB+PM的值最小时，求此时P的坐标．
25．（10分）求下列各式的值：
(1)已知 ，求代数式 的值；
(2)已知a=，求代数式[(ab+1) (ab- 2) - 2a2b2 +2] (-ab)的值．
26．（10分）列分式方程解应用题.
为缓解市区至通州沿线的通勤压力，北京市政府利用既有国铁线路富余能力，通过线路及站台改造，开通了“京通号”城际动车组，每班动车组预定运送乘客1200人，为提高运输效率，“京通号”车组对动车车厢进行了改装，使得每节车厢乘坐的人数比改装前多了，运送预定数量的乘客所需要的车厢数比改装前减少了4节，求改装后每节车厢可以搭载的乘客人数.
参考答案
一、选择题(每小题3分,共30分)
1、D
【解析】根据题意得出甲的效率为、乙的效率为，再根据工作时间=工作量÷甲乙合作的工作效率可得答案．
【详解】根据题意，甲、乙合做这项工程所需的时间为=，
故选D．
【点睛】
本题主要考查列代数式，解题的关键是掌握工程问题中的基本关系式及代数式的书写规范．
2、D
【分析】根据全等三角形的判定定理判断即可．
【详解】A、在△ABC和△DCB中
∴△ABC≌△DCB，故本选项正确；
B、在△ABC和△DCB中
∴△ABC≌△DCB，故本选项正确；
C、∵
∴
在△ABC和△DCB中
∴△ABC≌△DCB，故本选项正确；
D、根据两边和其中一边的对角不能判断两三角形全等；故本选项错误；
故选：D．
【点睛】
本题主要考查对全等三角形的判定的理解和掌握，能熟练地根据等腰三角形的性质及全等三角形的判定定理进行证明是解此题的关键．
3、C
【分析】根据全等三角形的对应边相等和全等三角形的对应角相等，可得第二个三角形没有标注的边为a，且a和c的夹角为70°，利用三角形的内角和定理即可求出∠1．
【详解】解：∵两个三角形全等，
∴第二个三角形没有标注的边为a，且a和c的夹角为70°
∴∠1=180°－70°－50°=60°
故选C．
【点睛】
此题考查的是全等三角形的性质，掌握全等三角形的对应边相等和全等三角形的对应角相等是解决此题的关键．
4、B
【分析】根据平面直角坐标系中点P(a,b)，①第一象限：a>1，b>1；②第二象限：a1；③第三象限：a1；②第二象限：a1；③第三象限：a