冀教版数学九上 期末　学情评估卷

这是一份冀教版数学九上 期末　学情评估卷，共15页。试卷主要包含了解答题17.解下列方程等内容，欢迎下载使用。
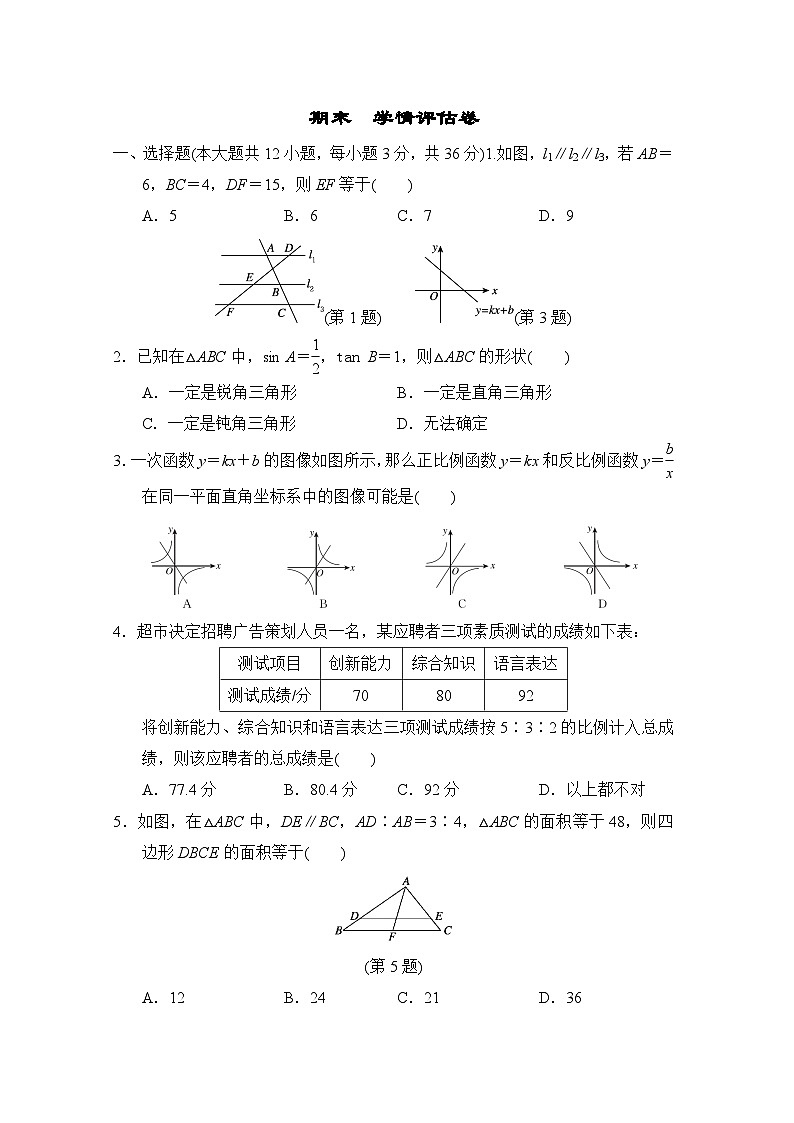
A．5 B．6 C．7 D．9
(第1题) (第3题)
2．已知在△ABC中，sin A＝eq \f(1,2)，tan B＝1，则△ABC的形状( )
A．一定是锐角三角形 B．一定是直角三角形
C．一定是钝角三角形 D．无法确定
3．一次函数y＝kx＋b的图像如图所示，那么正比例函数y＝kx和反比例函数y＝eq \f(b,x)在同一平面直角坐标系中的图像可能是( )
4．超市决定招聘广告策划人员一名，某应聘者三项素质测试的成绩如下表：
将创新能力、综合知识和语言表达三项测试成绩按5∶3∶2的比例计入总成绩，则该应聘者的总成绩是( )
A．77.4分 B．80.4分 C．92分 D．以上都不对
5．如图，在△ABC中，DE∥BC，AD∶AB＝3∶4，△ABC的面积等于48，则四边形DBCE的面积等于( )
(第5题)
A．12 B．24 C．21 D．36
6．已知m，n是一元二次方程x2＋3x－2＝0的两个根，则eq \f(3,m－n)－eq \f(6n,m2－n2)的值是( )
A．1 B．－1 C.eq \f(3,2) D．－eq \f(3,2)
7．在平面直角坐标系中，△ABC的顶点坐标分别是A(1，2)，B(1，1)，C(3，1)，以原点O为位似中心，作△ABC的位似图形△DEF，若△DEF与△ABC的相似比为3∶1，则点F的坐标为( )
A．(2，4)或(－2，－4) B．(9，3)或(－9，－3)
C．(6，2)或(－6，－2) D．(7，2)
8．一次综合实践的主题为：“只用一张矩形纸条和刻度尺，如何测量一次性纸杯杯口的直径？”小聪同学所在的学习小组想到了如下方法：如图，将纸条拉直并紧贴杯口，纸条的上下边沿分别与杯口相交于A、B、C、D四点，然后利用刻度尺量得该纸条的宽为7 cm，AB＝8 cm，CD＝6 cm.请你帮忙计算纸杯的直径为( )
A．5 cm B．9.6 cm C．10 cm D．10.2 cm
9．我国古代数学家研究过一元二次方程的正数解的几何解法．以方程x2＋5x－14＝0，即x(x＋5)＝14为例说明，《方图注》中记载的方法是：构造如图所示的大正方形，大正方形的面积是(x＋x＋5)2，同时它又等于四个矩形的面积加上中间小正方形的面积，即4×14＋52，因此x＝2.小明用此方法解关于x的方程x2＋mx－n＝0时，构造出同样的图形，已知大正方形的面积为14，小正方形的面积为4，则( )
A．m＝2，n＝3 B．m＝eq \f(\r(14),2)，n＝2
C．m＝eq \f(5,2)，n＝2 D．m＝2，n＝eq \f(5,2)
(第9题) (第10题)
10．如图，在Rt△ABC中，∠C＝90°，BC＝eq \r(5)，点D是AC上一点，连接BD.若tan A＝eq \f(1,3)，tan ∠CDB＝eq \f(1,2)，则AD的长为( )
A．2 B.eq \r(5) C．3 D．2 eq \r(5)
11．如图，在⊙O中，直径AB与弦CD相交于点E，连接弦BC，BD，AD.若∠ABC＝2∠ABD.给出下列结论：①BC＝BE；②2AD2＝AE·AB，则下列判断正确的是( )
(第11题)
A．①，②都对 B．①，②都错
C．①对，②错 D．①错，②对
12．在平面直角坐标系中，横、纵坐标都是整数的点叫做整点，已知函数y＝eq \f(k,x)(x＞0)的图像G经过点A(4，1)，直线l：y＝eq \f(1,3)x＋b与图像G交于点B，与y轴交于点C.记图像G在点A，B之间的部分与线段OA，OC，BC围成的区域(不含边界)为W，若区域W内恰有4个整点，则b的取值范围是( )
A．－eq \f(5,3)＜b≤－eq \f(4,3) B.eq \f(5,3)＜b≤eq \f(8,3)
C．－eq \f(5,3)≤b＜－eq \f(4,3)或eq \f(5,3)＜b≤eq \f(8,3) D．－eq \f(5,3)＜b≤－eq \f(4,3)或eq \f(5,3)≤b＜eq \f(8,3)
二、填空题(本大题共4小题，每小题3分，共12分)13.如图，有一长为4，宽为3的长方形木板在桌面上做无滑动的翻滚(顺时针方向)．木板上的顶点A的位置变化为A→A1→A2，其中第二次翻滚被桌面上一小木块挡住，此时∠A1CA2＝60°，则点A翻滚到A2位置时，走过的路径长为______________．
(第13题) (第14题)
14．如图，梯形ABCD是拦水坝的横断面(图中i＝1∶eq \r(3)是指坡面的铅直高度DE与水平宽度CE的比)．∠B＝60°，AB＝6，AD＝4，则拦水坝的横断面ABCD的面积是________．(结果保留整数，参考数据：eq \r(3)≈1.732)
15．已知关于x的一元二次方程(a－3)x2－8x＋9＝0.若方程的一个根为x＝－1，则a的值为 ________；若方程有实数根，则满足条件的正整数a的值为____________．
16．定义：若x，y满足x2＝4y＋t，y2＝4x＋t且x≠y(t为常数)，则称点M(x，y)为“和谐点”．
(1)若P(3，m)是“和谐点”，则m＝________；
(2)若双曲线y＝eq \f(k,x)(－3＜x＜－1)存在“和谐点”，则k的取值范围为________．
三、解答题(本大题共8小题，共72分，解答时应写出文字说明、证明过程或演算步骤)17.(8分)解下列方程：
(1)x(x－2)＝2－x；
(2)2x2－4x＋1＝0(配方法)．
18．(8分)如图，在△ABD中，AC⊥BD，BC＝8，CD＝4，cs ∠ABC＝eq \f(4,5)，BF为AD边上的中线．
(1)求AC的长；
(2)求tan ∠FBD的值．
19．(8分)如图，把扇形OAB与扇形OCD的圆心重合叠放在一起，且∠AOB＝∠COD，连接AC，BD.
(1)求证：△AOC≌△BOD；
(2)若OA＝5 cm，OC＝3 cm，弧AB的长为3π cm，弧CD的长为1.8π cm，求阴影部分的面积；
(3)在(2)的条件下求由扇形OAB围成的圆锥的高．
20.(8分)某学校为调查九年级学生对“二十大”知识的了解情况，进行了“二十大”知识竞赛测试，从两班各随机抽取了10名学生的成绩，整理如下：(成绩得分用x表示，共分成四组：A.80≤x＜85，B.85≤x＜90，C.90≤x＜95，D.95≤x≤100)
九年级(1)班10名学生的成绩是：96，80，96，87，99，98，92，100，89，83.
九年级(2)班10名学生的成绩在C组中的数据是：94，90，92.
通过数据分析，绘制如下扇形统计图，并列表：
九年级(1)班、(2)班抽取的学生竞赛成绩统计表
根据以上信息，解答下列问题：
(1)直接写出上述a，b，c的值：a＝________，b＝________，c＝________．
(2)学校欲选派成绩更稳定的班级参加下一阶段的活动，根据表格中的数据，学校会选派哪一个班级？说明理由．
(3)九年级两个班共120名学生参加了此次调查活动，估计两个班参加此次调查活动成绩优秀(x≥90)的学生总人数是多少？
21．(8分)如图，老李想用长为70 m的栅栏，再借助房屋的外墙(外墙足够长)围成一个矩形羊圈ABCD，并在边BC上留一个2 m宽的门(建在EF处，另用其他材料)．
(1)当羊圈的边AB的长为多少米时，能围成一个面积为640 m2的羊圈？
(2)羊圈的面积能达到650 m2吗？如果能，请你给出设计方案；如果不能，请说明理由．
22．(10分)贵州旅游资源丰富．某景区为给游客提供更好的游览体验，拟在如图①景区内修建观光索道．设计示意图如图②所示，以山脚A为起点，沿途修建AB，CD两段长度相等的观光索道，最终到达山顶D处，中途设计了一段与AF平行的观光平台BC为50 m．索道AB与AF的夹角为15°，CD与水平线的夹角为45°，A，B两处的水平距离AE为576 m，DF⊥AF，垂足为点F.(图中所有点都在同一平面内，点A，E，F在同一水平线上)
(1)求索道AB的长(结果精确到1 m)；
(2)求水平距离AF的长(结果精确到1 m)．
(参考数据：sin 15°≈0.26，cs 15°≈0.97，tan 15°≈0.27，eq \r(2)≈1.41)
23．(10分)心理学家研究发现，一般情况下，一节课40分钟中，学生的注意力随教师讲课的变化而变化．开始上课时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散．经过实验分析可知，学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB，BC分别为线段，CD为双曲线的一部分)：
(1)求y与x之间的函数关系式．
(2)开始上课后第5分钟时与第30分钟时相比较，何时学生的注意力更集中？
(3)一道数学竞赛题，需要讲19分钟，为了效果较好，要求学生的注意力指标数最低达到36，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目？说明理由．
24．(12分)如图，在矩形ABCD中，点E在边CD上，M是线段AD上任意一点，直线EM与直线AB相交于点N，射线MP与边CB相交于点P，且MP⊥EN.已知AB＝5，AD＝8，DE＝3，DM＝x，完成以下问题：
(1)如图①，当x＝4.8时，AN＝________．
(2)①如图②，当点P与点B重合时，求tan ∠DME的值．
②如图③，当x＝4时，求线段PB的长．
(3)直接写出S△EPN的值．(用含有x的代数式表示)
答案
一、选择题
二、填空题
13.eq \f(7π,2) 14.52 15.－14；4或2或1
16．(1)－7 (2)3＜k＜4
三、解答题
17．解：(1)由x(x－2)＝2－x，得x(x－2)＋x－2＝0，
因式分解，得(x＋1)(x－2)＝0，解得x1＝－1，x2＝2.
(2)原方程变形，得2x2－4x＝－1，
系数化为1，得x2－2x＝－eq \f(1,2)，
配方，得x2－2x＋(－1)2＝1－eq \f(1,2)，∴(x－1)2＝eq \f(1,2)，
∴x－1＝±eq \f(\r(2),2)，解得x1＝1＋eq \f(\r(2),2)，x2＝1－eq \f(\r(2),2).
18．解：(1)∵AC⊥BD，cs ∠ABC＝eq \f(4,5).
∴cs ∠ABC＝eq \f(BC,AB)＝eq \f(4,5).∴AB＝eq \f(5,4)BC＝10.
∴AC＝eq \r(AB2－BC2)＝6.
(2)过点F作FG⊥BD于点G，
∵BF为AD边上的中线，
∴F是AD的中点，即eq \f(DF,AD)＝eq \f(1,2).
∵FG⊥BD，AC⊥BD，∴FG∥AC.
∴△DFG∽△DAC.∴eq \f(FG,AC)＝eq \f(DG,CD)＝eq \f(DF,AD)＝eq \f(1,2).
∴FG＝eq \f(1,2)AC＝3，DG＝CG＝eq \f(1,2)CD＝2.
∴在Rt△BFG中，tan ∠FBD＝eq \f(FG,BG)＝eq \f(3,8＋2)＝eq \f(3,10).
19．(1)证明：∵∠COD＝∠AOB，
∴∠AOC＋∠AOD＝∠AOD＋∠BOD.
∴∠AOC＝∠BOD.
在△AOC和△BOD中，∵eq \b\lc\{(\a\vs4\al\c1(OC＝OD，,∠AOC＝∠BOD，,OA＝OB，))
∴△AOC≌△BOD(SAS)．
(2)解：∵△AOC≌△BOD，
∴S△AOC＝S△BOD.
∴S阴影＝S扇形OAB＋S△AOC－S扇形OCD－S△BOD＝S扇形OAB－S扇形OCD＝eq \f(1,2)×5×3π－eq \f(1,2)×3×1.8π＝4.8π(cm2)．
∴阴影部分的面积是4.8πcm2.
(3)解：围成的圆锥底面圆的半径为eq \f(3π,2π)＝1.5(cm)，母线长为5 cm，∴圆锥的高＝eq \r(52－1.52)＝eq \f(\r(91),2)(cm)．
20．解：(1)40；94；96
(2)选派九年级(1)班，理由如下：
∵两个班的平均成绩相同，而九年级(1)班的方差为44，九年级(2)班的方差为50.4，44＜50.4，
∴九年级(1)班成绩更稳定．
∴学校会选派九年级(1)班．
(3)∵九年级(2)班D组的人数为10×40%＝4(名)，
∴九年级(2)班10名学生的成绩为优秀的人数为3＋4＝7(名)．
又∵九年级(1)班10名学生的成绩为优秀的人数为6(名)，
∴估计两个班参加此次调查活动成绩优秀(x≥90)的学生总人数是120×eq \f(6＋7,10＋10)＝78(名)．
21．解：(1)设羊圈的边AB的长为x m，则边BC的长为(72－2x)m，根据题意，得x(72－2x)＝640，
化简，得x2－36x＋320＝0，
解方程，得x1＝16，x2＝20，当x1＝16时，72－2x＝40，
当x2＝20时，72－2x＝32.
答：当羊圈的边AB的长为16 m或20 m时，能围成一个面积为640 m2的羊圈．
(2)不能，理由如下：根据题意，得x(72－2x)＝650，
化简，得x2－36x＋325＝0，
∵b2－4ac＝(－36)2－4×325＝－4＜0，
∴该方程没有实数根．∴羊圈的面积不能达到650 m2.
22．解：(1)在Rt△ABE中，∠AEB＝90°，∠A＝15°，AE＝576 m，
∴AB＝eq \f(AE,cs A)＝eq \f(576,cs 15°)≈594(m)．
答：索道AB的长约为594 m.
(2)延长BC交DF于点G，
∵BC∥AF，DF⊥AF，
∴DG⊥CG.∴四边形BEFG为矩形．∴EF＝BG.
∵CD＝AB≈594 m，∠DCG＝45°，
∴CG＝CD·cs ∠DCG≈594×cs 45°＝297 eq \r(2).
∴AF＝AE＋EF＝AE＋BG＝AE＋BC＋CG≈576＋50＋297 eq \r(2)≈1 045(m)．
答：水平距离AF的长约为1 045 m.
23．解：(1)当0≤x≤10时，设线段AB所在的直线的表达式为y1＝k1x＋20(k1≠0)，把B(10，40)代入，得k1＝2，
∴y1＝2x＋20；当10＜x≤25时，y2＝40；
当x＞25时，设CD所在双曲线的表达式为y3＝eq \f(k3,x)(k3≠0)，把C(25，40)代入，得k3＝1 000，
∴y3＝eq \f(1 000,x).
∴y与x之间的函数关系式为y＝eq \b\lc\{(\a\vs4\al\c1(2x＋20（0≤x≤10），,40（10＜x≤25），,\f(1 000,x)（x＞25）.))
(2)当x＝5时，y＝2×5＋20＝30；
当x＝30时，y＝eq \f(1 000,30)＝eq \f(100,3)，
∵3019，∴经过适当安排，老师能在学生注意力达到所需的状态下讲解完这道题目．
24．解：(1)2
(2)①∵四边形ABCD是矩形，∴∠D＝∠BAM＝90°.
∴∠DME＋∠DEM＝90°.
∵MP⊥EN，∴∠BME＝90°.
∴∠AMB＋∠DME＝90°.∴∠DEM＝∠AMB.
∴△DEM∽△AMB.∴eq \f(DM,AB)＝eq \f(DE,AM)，即eq \f(DM,5)＝eq \f(3,8－DM)，
解得DM＝5或DM＝3，经检验DM＝5或DM＝3都是方程的解，∴tan ∠DME＝eq \f(DE,DM)＝eq \f(3,5)或tan ∠DME＝eq \f(DE,DM)＝eq \f(3,3)＝1.∴tan ∠DME的值为eq \f(3,5)或1.
②由题易知∠MAN＝∠D＝90°，
又∵∠DME＝∠AMN，
∴△DEM∽△ANM，
∴eq \f(AN,DE)＝eq \f(AM,DM)，
∴eq \f(AN,3)＝eq \f(8－4,4)，解得AN＝3，
∴在Rt△AMN中，MN＝eq \r(AN2＋AM2)＝eq \r(32＋42)＝5，
如图，设射线MP与直线AB交于点Q，
∵MP⊥EN，∴∠NMQ＝90°.
∴∠NAM＝∠NMQ.
∵∠ANM＝∠MNQ，
∴△ANM∽△MNQ.∴eq \f(MN,QN)＝eq \f(AN,MN).
∴eq \f(5,QN)＝eq \f(3,5)，解得QN＝eq \f(25,3).
∴BQ＝QN－AN－AB＝eq \f(25,3)－3－5＝eq \f(1,3).
∵四边形ABCD是矩形，∴BP∥AM.
∴△QBP∽△QAM.∴eq \f(BQ,AQ)＝eq \f(BP,AM).
∴eq \f(\f(1,3),5＋\f(1,3))＝eq \f(BP,4).解得BP＝eq \f(1,4)，故线段PB的长为eq \f(1,4).
(3)20＋eq \f(180,x2). 解析：如图，连接PE，PN.
∵DM＝x，
∴AM＝8－x，由(2)②得eq \f(AN,DE)＝eq \f(AM,DM)，
∴eq \f(AN,3)＝eq \f(8－x,x)，解得AN＝eq \f(24－3x,x).
∵∠NMQ＝90°，
∴∠AMN＋∠AMQ＝90°.
∵∠ANM＋∠AMN＝90°，∴∠ANM＝∠AMQ.
∵∠MAN＝∠QAM＝90°，∴△MAN∽△QAM.
∴eq \f(AM,AQ)＝eq \f(AN,AM)，∴eq \f(8－x,5＋BQ)＝eq \f(\f(24－3x,x),8－x)，
解得BQ＝eq \f(－x2＋8x－15,3)，由(2)②得eq \f(BQ,AQ)＝eq \f(BP,AM)，
∴eq \f(\f(－x2＋8x－15,3),5＋\f(－x2＋8x－15,3))＝eq \f(BP,8－x)，解得BP＝eq \f(－x2＋8x－15,x)，
∴CP＝8－eq \f(－x2＋8x－15,x)＝eq \f(x2＋15,x).
∵CE＝5－3＝2，BN＝5＋eq \f(24－3x,x)＝eq \f(24＋2x,x)，
∴S△EPN＝S梯形△ECBN－S△PCE－S△NBP＝eq \f(1,2)BC(CE＋BN)－eq \f(1,2)CE·CP－eq \f(1,2)BN·BP＝eq \f(1,2)×8×eq \b\lc\(\rc\)(\a\vs4\al\c1(2＋\f(24＋2x,x)))－eq \f(1,2)×2×eq \f(x2＋15,x)－eq \f(1,2)×eq \f(24＋2x,x)×eq \f(－x2＋8x－15,x)＝20＋eq \f(180,x2).
测试项目
创新能力
综合知识
语言表达
测试成绩/分
70
80
92
年级
平均数
中位数
众数
方差
九年级(1)班
92
b
c
44
九年级(2)班
92
93
100
50.4
答案
速查
1
2
3
4
5
6
7
8
9
10
11
12
B
C
D
A
C
B
B
C
D
B
A
B