新高考数学二轮复习培优专题训练专题12 运用空间向量研究立体几何问题（1）（2份打包，原卷版+解析版）

这是一份新高考数学二轮复习培优专题训练专题12 运用空间向量研究立体几何问题（1）（2份打包，原卷版+解析版），文件包含新高考数学二轮复习培优专题训练专题12运用空间向量研究立体几何问题1原卷版doc、新高考数学二轮复习培优专题训练专题12运用空间向量研究立体几何问题1解析版doc等2份试卷配套教学资源，其中试卷共51页， 欢迎下载使用。
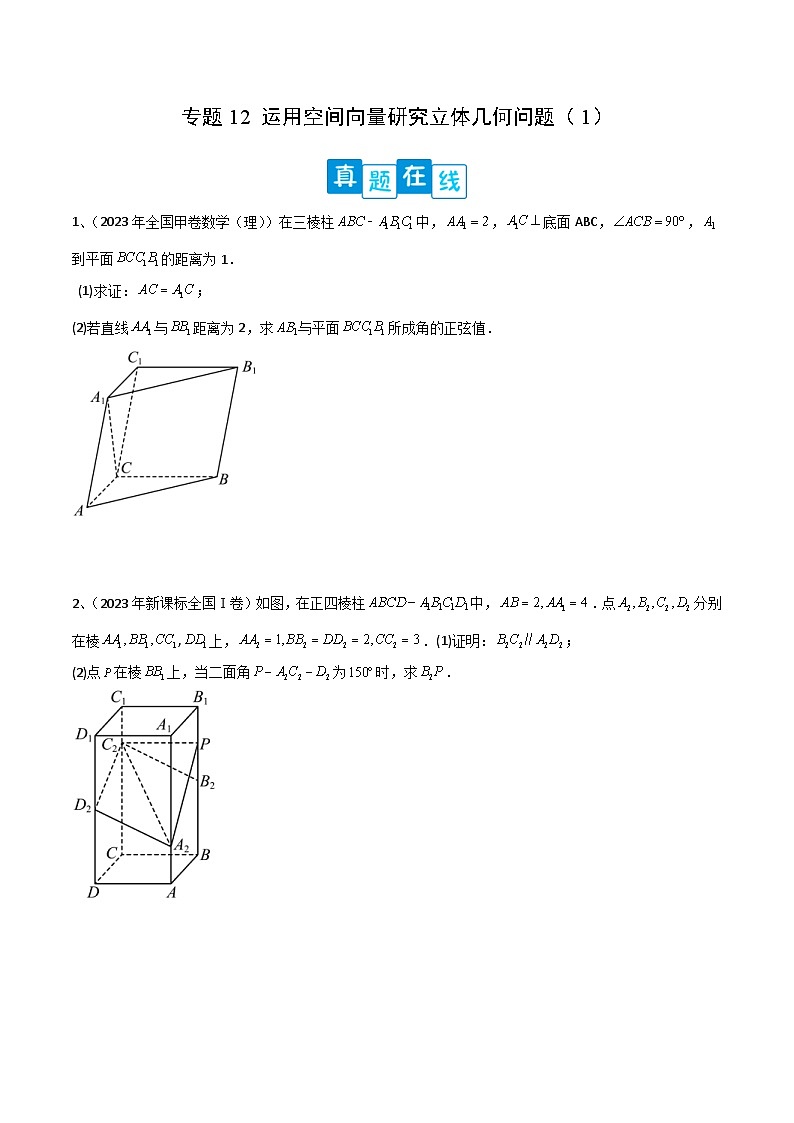
1、（2023年全国甲卷数学（理））在三棱柱 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 底面ABC， SKIPIF 1 < 0 ， SKIPIF 1 < 0 到平面 SKIPIF 1 < 0 的距离为1．
(1)求证： SKIPIF 1 < 0 ；
(2)若直线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 距离为2，求 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的正弦值．
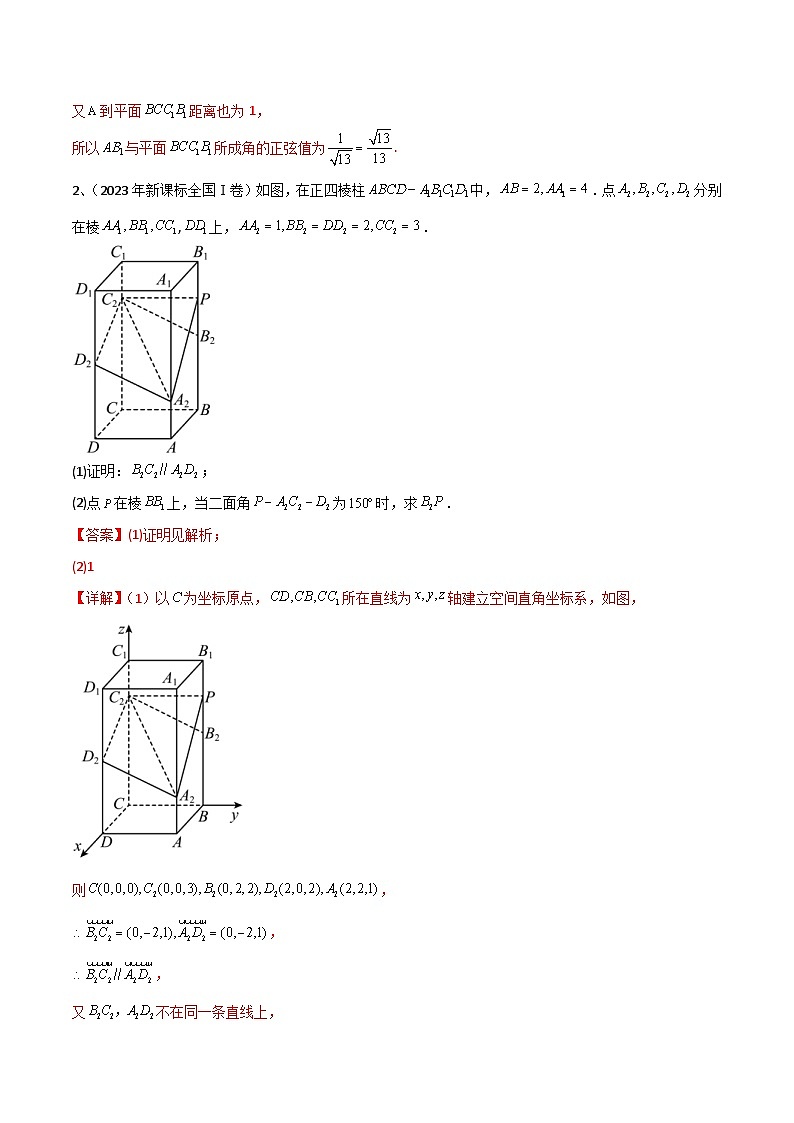
2、（2023年新课标全国Ⅰ卷）如图，在正四棱柱 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ．点 SKIPIF 1 < 0 分别在棱 SKIPIF 1 < 0 , SKIPIF 1 < 0 上， SKIPIF 1 < 0 ．(1)证明： SKIPIF 1 < 0 ；
(2)点 SKIPIF 1 < 0 在棱 SKIPIF 1 < 0 上，当二面角 SKIPIF 1 < 0 为 SKIPIF 1 < 0 时，求 SKIPIF 1 < 0 ．
3、（2023年新课标全国Ⅱ卷）如图，三棱锥 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，E为BC的中点．(1)证明： SKIPIF 1 < 0 ；
(2)点F满足 SKIPIF 1 < 0 ，求二面角 SKIPIF 1 < 0 的正弦值．
4、（2023年全国乙卷数学(理)（文））如图，在三棱锥 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，BP，AP，BC的中点分别为D，E，O， SKIPIF 1 < 0 ，点F在AC上， SKIPIF 1 < 0 .
(1)证明： SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)证明：平面 SKIPIF 1 < 0 平面BEF；
(3)求二面角 SKIPIF 1 < 0 的正弦值.
5、【2022年全国甲卷】在四棱锥中，底面．
(1)证明：；
(2)求PD与平面所成的角的正弦值．
6、【2022年全国乙卷】如图，四面体中，，E为的中点．
(1)证明：平面平面；
(2)设，点F在上，当的面积最小时，求与平面所成的角的正弦值．
7、【2022年新高考1卷】如图，直三棱柱的体积为4，的面积为．
(1)求A到平面的距离；
(2)设D为的中点，，平面平面，求二面角的正弦值．
8、【2022年新高考2卷】如图，是三棱锥的高，，，E是的中点．
(1)证明：平面；
(2)若，，，求二面角的正弦值．
题组一、线面角
1-1、（2023·安徽宿州·统考一模）如图，四棱锥 SKIPIF 1 < 0 中， SKIPIF 1 < 0 底面ABCD， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 为棱 SKIPIF 1 < 0 靠近点 SKIPIF 1 < 0 的三等分点.
(1)证明： SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)求 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成的角的正弦值.
1-2、（2023·吉林通化·梅河口市第五中学校考一模）如图，在正三棱柱 SKIPIF 1 < 0 中，D为棱 SKIPIF 1 < 0 上的点，E，F，G分别为AC， SKIPIF 1 < 0 ， SKIPIF 1 < 0 的中点， SKIPIF 1 < 0 ．(1)求证： SKIPIF 1 < 0 ；
(2)若直线FG与平面BCD所成角的正弦值为 SKIPIF 1 < 0 ，求AD的长．
1-3、（2023·山西晋中·统考三模）如图，在四棱锥P-ABCD中，底面ABCD为矩形，E是CD的中点，AE与BD交于点F，G是 SKIPIF 1 < 0 的重心．
(1)求证： SKIPIF 1 < 0 平面PCD；
(2)若平面PAD⊥平面ABCD， SKIPIF 1 < 0 为等腰直角三角形，且 SKIPIF 1 < 0 ，求直线AG与平面PBD所成角的正弦值．
题组二、面面角
2-1、（2023·黑龙江大庆·统考一模）如图，在长方体 SKIPIF 1 < 0 中，底面 SKIPIF 1 < 0 是边长为2的正方形， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 分别是 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的中点.(1)证明： SKIPIF 1 < 0 ∥平面 SKIPIF 1 < 0 ；
(2)求平面 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 夹角的余弦值.
2-2、（2023·山西临汾·统考一模）在三棱锥 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，取直线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的方向向量分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 与 SKIPIF 1 < 0 夹角为 SKIPIF 1 < 0 .
(1)求证： SKIPIF 1 < 0 ；
(2)求平面 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 的夹角的余弦值.
2-3、（2023·云南红河·统考一模）如图，在多面体ABCDEF中，A，B，C，D四点共面， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，AF⊥平面ABCD， SKIPIF 1 < 0 ．
(1)求证：CD⊥平面ADF；
(2)若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求平面 SKIPIF 1 < 0 和平面 SKIPIF 1 < 0 的夹角的余弦值．
题组三、线面角与面面角的综合
3-1、（2023·湖南邵阳·统考三模）如图所示，在直四棱柱ABCD- SKIPIF 1 < 0 中，底面ABCD为菱形， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，E为线段 SKIPIF 1 < 0 上一点.
(1)求证： SKIPIF 1 < 0 ；
3-2、（2023·湖南岳阳·统考三模）如图，在三棱柱 SKIPIF 1 < 0 中，D为AC的中点，AB=BC=2， SKIPIF 1 < 0 .
(1)证明： SKIPIF 1 < 0 ；
(2)若 SKIPIF 1 < 0 ，且满足：三棱柱 SKIPIF 1 < 0 的体积为 SKIPIF 1 < 0 ，二面角 SKIPIF 1 < 0 的大小为60°，求二面角 SKIPIF 1 < 0 的正弦值.
1、（2022·山东青岛·高三期末）如图所示，已知四棱锥P-ABCD的底面是矩形， SKIPIF 1 < 0 底面ABCD，M为BC中点，且 SKIPIF 1 < 0 .
（1）求证：面 SKIPIF 1 < 0 面PDB；
（2）若两条异面直线AB与PC所成的角为45°，求面PAM与面PBC夹角的余弦值.
2、（2022·山东德州·高三期末）如图，在直三棱柱 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，点Q为BC的中点，平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 .
（1）证明： SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
（2）若直线AC与平面 SKIPIF 1 < 0 所成角的大小为30°，求锐二面角 SKIPIF 1 < 0 的大小.
3、（2023·黑龙江·黑龙江实验中学校考一模）如图，在四棱锥 SKIPIF 1 < 0 中，四边形ABCD是直角梯形， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 底面ABCD， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，E是PB的中点．
(1)求证：平面 SKIPIF 1 < 0 平面PBC；
(2)若二面角 SKIPIF 1 < 0 的余弦值为 SKIPIF 1 < 0 ，求a的值；
(3)在（2）的条件下求直线PA与平面EAC所成角的正弦值．
4、（2023·湖北·校联考三模）已知平行六面体（底面是平行四边形的四棱柱） SKIPIF 1 < 0 的各条棱长均为2，且有 SKIPIF 1 < 0 ．
(1)求证：平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)求直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的正弦值．
5、（2023·江苏连云港·统考模拟预测）如图，直三棱柱 SKIPIF 1 < 0 内接于圆柱， SKIPIF 1 < 0 ，平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ．
(1)证明： SKIPIF 1 < 0 为圆柱底面的直径；
(2)若M为 SKIPIF 1 < 0 中点，N为 SKIPIF 1 < 0 中点，求平面 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成锐二面角的余弦值．
6、（2023·江苏南通·统考一模）如图，在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 是 SKIPIF 1 < 0 边上的高，以 SKIPIF 1 < 0 为折痕，将 SKIPIF 1 < 0 折至 SKIPIF 1 < 0 的位置，使得 SKIPIF 1 < 0 .
(1)证明： SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)若 SKIPIF 1 < 0 ，求二面角 SKIPIF 1 < 0 的正弦值.