新高考数学二轮复习培优专题训练专题14 空间几何体的折叠及多面体的问题（2份打包，原卷版+解析版）

这是一份新高考数学二轮复习培优专题训练专题14 空间几何体的折叠及多面体的问题（2份打包，原卷版+解析版），文件包含新高考数学二轮复习培优专题训练专题14空间几何体的折叠及多面体的问题原卷版doc、新高考数学二轮复习培优专题训练专题14空间几何体的折叠及多面体的问题解析版doc等2份试卷配套教学资源，其中试卷共39页， 欢迎下载使用。

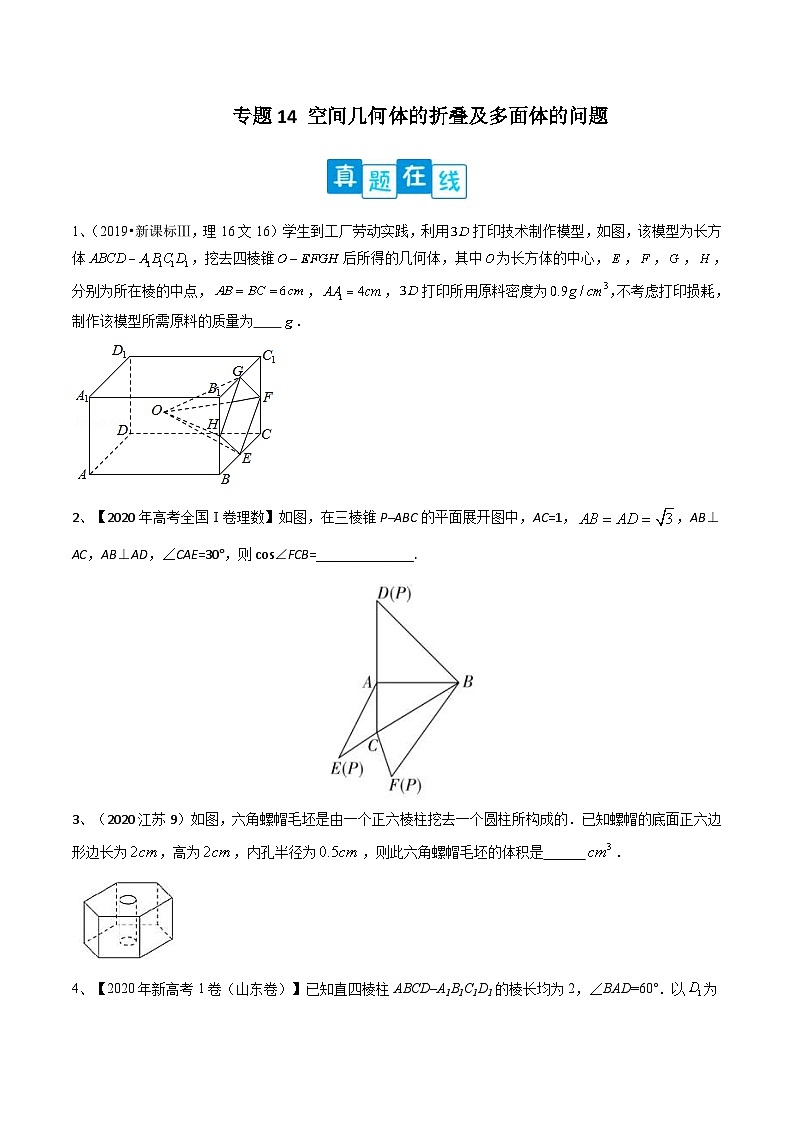
1、（2019•新课标Ⅲ，理16文16）学生到工厂劳动实践，利用 SKIPIF 1 < 0 打印技术制作模型，如图，该模型为长方体 SKIPIF 1 < 0 ，挖去四棱锥 SKIPIF 1 < 0 后所得的几何体，其中 SKIPIF 1 < 0 为长方体的中心， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，分别为所在棱的中点， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 打印所用原料密度为 SKIPIF 1 < 0 ，不考虑打印损耗，制作该模型所需原料的质量为 SKIPIF 1 < 0 ．
2、【2020年高考全国Ⅰ卷理数】如图，在三棱锥P–ABC的平面展开图中，AC=1， SKIPIF 1 < 0 ，AB⊥AC，AB⊥AD，∠CAE=30°，则cs∠FCB=______________.
3、（2020江苏9）如图，六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的．已知螺帽的底面正六边形边长为 SKIPIF 1 < 0 ，高为 SKIPIF 1 < 0 ，内孔半径为 SKIPIF 1 < 0 ，则此六角螺帽毛坯的体积是 SKIPIF 1 < 0 ．
4、【2020年新高考1卷（山东卷）】已知直四棱柱ABCD–A1B1C1D1的棱长均为2，∠BAD=60°．以 SKIPIF 1 < 0 为球心， SKIPIF 1 < 0 为半径的球面与侧面BCC1B1的交线长为________．
5、【2019年新课标2卷理科】中国有悠久的金石文化，印信是金石文化的代表之一．印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”（图1）.半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美．图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1．则该半正多面体共有________个面，其棱长为_________．
题组一、 几何体的多边形问题
1-1、（2023·河北沧州·校考模拟预测）如图所示，该几何体由一个直三棱柱 SKIPIF 1 < 0 和一个四棱锥 SKIPIF 1 < 0 组成， SKIPIF 1 < 0 ，则下列说法正确的是（ ）
A．若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
B．若平面 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 的交线为 SKIPIF 1 < 0 ，则AC//l
C．三棱柱 SKIPIF 1 < 0 的外接球的表面积为 SKIPIF 1 < 0
D．当该几何体有外接球时，点 SKIPIF 1 < 0 到平面 SKIPIF 1 < 0 的最大距离为 SKIPIF 1 < 0
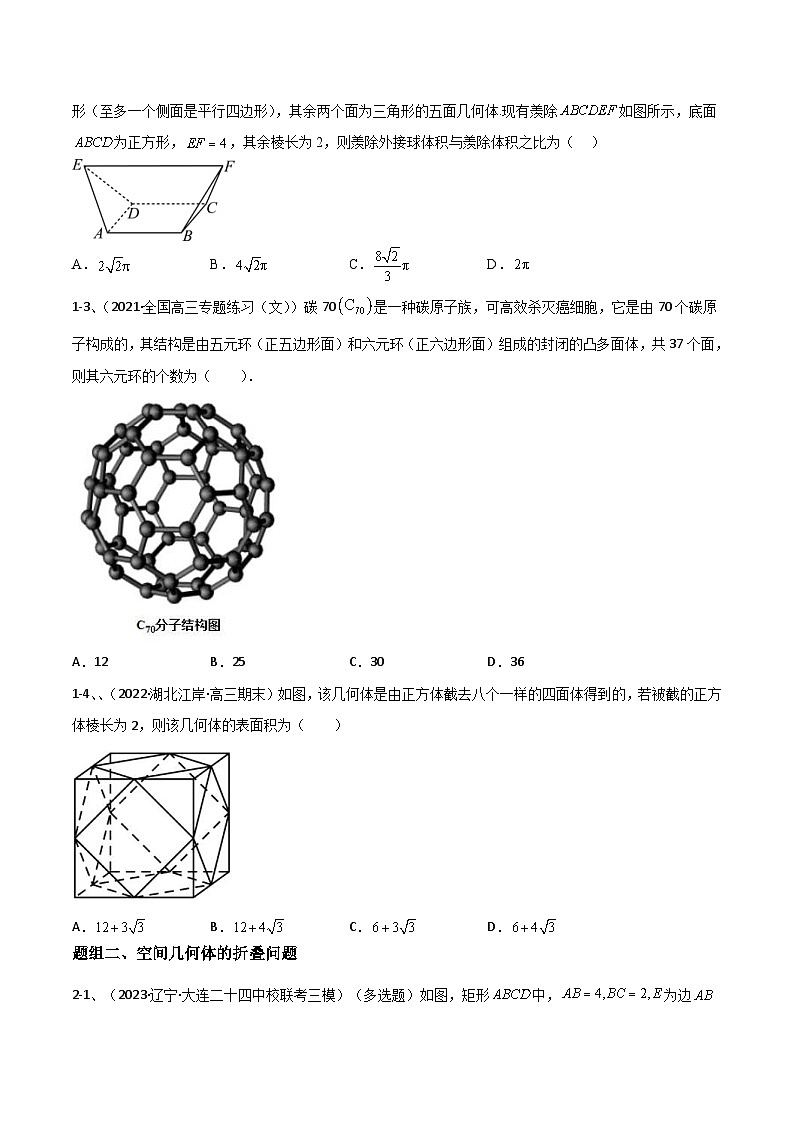
1-2、（2023·山西临汾·统考一模）《九章算术·商功》提及一种称之为“羡除”的几何体，刘徽对此几何体作注：“羡除，隧道也其所穿地，上平下邪.似两鳖臑夹一堑堵，即羡除之形.”羡除即为：三个面为梯形或平行四边形（至多一个侧面是平行四边形），其余两个面为三角形的五面几何体.现有羡除 SKIPIF 1 < 0 如图所示，底面 SKIPIF 1 < 0 为正方形， SKIPIF 1 < 0 ，其余棱长为2，则羡除外接球体积与羡除体积之比为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
1-3、（2021·全国高三专题练习（文））碳70是一种碳原子族，可高效杀灭癌细胞，它是由70个碳原子构成的，其结构是由五元环（正五边形面）和六元环（正六边形面）组成的封闭的凸多面体，共37个面，则其六元环的个数为（ ）．
A．12B．25C．30D．36
1-4、、（2022·湖北江岸·高三期末）如图，该几何体是由正方体截去八个一样的四面体得到的，若被截的正方体棱长为2，则该几何体的表面积为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
题组二、空间几何体的折叠问题
2-1、（2023·辽宁·大连二十四中校联考三模）（多选题）如图，矩形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 为边 SKIPIF 1 < 0 的中点，沿 SKIPIF 1 < 0 将 SKIPIF 1 < 0 折起，点 SKIPIF 1 < 0 折至 SKIPIF 1 < 0 处（ SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ），若 SKIPIF 1 < 0 为线段 SKIPIF 1 < 0 的中点，二面角 SKIPIF 1 < 0 大小为 SKIPIF 1 < 0 ，直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角为 SKIPIF 1 < 0 ，则在 SKIPIF 1 < 0 折起过程中，下列说法正确的是（ ）
A．存在某个位置，使得 SKIPIF 1 < 0
B． SKIPIF 1 < 0 面积的最大值为 SKIPIF 1 < 0
C．当 SKIPIF 1 < 0 为锐角时，存在某个位置，使得 SKIPIF 1 < 0
D．三棱锥 SKIPIF 1 < 0 体积最大时，三棱锥 SKIPIF 1 < 0 的外接球的表面积为 SKIPIF 1 < 0
2-2、（2023·云南红河·统考一模）如图所示是一块边长为10cm的正方形铝片，其中阴影部分由四个全等的等腰梯形和一个正方形组成，将阴影部分裁剪下来，并将其拼接成一个无上盖的容器（铝片厚度不计），则该容器的容积为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
2-3、（2022·江苏宿迁·高三期末）如图，一张长､宽分别为 SKIPIF 1 < 0 的矩形纸， SKIPIF 1 < 0 ， SKIPIF 1 < 0 分别是其四条边的中点.现将其沿图中虚线折起，使得 SKIPIF 1 < 0 四点重合为一点 SKIPIF 1 < 0 ，从而得到一个多面体，则（ ）
A．在该多面体中， SKIPIF 1 < 0
B．该多面体是三棱锥
C．在该多面体中，平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0
D．该多面体的体积为 SKIPIF 1 < 0
2-4、（2022·江苏扬州·高三期末）在边长为6的正三角形ABC中M，N分别为边AB，AC上的点，且满足 SKIPIF 1 < 0 ，把△AMN沿着MN翻折至A′MN位置，则下列说法中正确的有（ ）
A．在翻折过程中，在边A′N上存在点P，满足CP∥平面A′BM
B．若 SKIPIF 1 < 0 ，则在翻折过程中的某个位置，满足平面A′BC⊥平面BCNM
C．若 SKIPIF 1 < 0 且二面角A′－MN－B的大小为120°，则四棱锥A′－BCNM的外接球的表面积为61π
D．在翻折过程中，四棱锥A′－BCNM体积的最大值为 SKIPIF 1 < 0
题组三、运用空间向量解决空间几何体的折叠问题
3-1、（2023·广东佛山·统考模拟预测）如图 SKIPIF 1 < 0 ，菱形 SKIPIF 1 < 0 的边长为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，将 SKIPIF 1 < 0 沿 SKIPIF 1 < 0 向上翻折，得到如图 SKIPIF 1 < 0 所示得三棱锥 SKIPIF 1 < 0 .

(1)证明： SKIPIF 1 < 0 ；
(2)若 SKIPIF 1 < 0 ，在线段 SKIPIF 1 < 0 上是否存在点 SKIPIF 1 < 0 ，使得平面 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的余弦值为 SKIPIF 1 < 0 ？若存在，求出 SKIPIF 1 < 0 ；若不存在，请说明理由.
3-2、（2023·河南·校联考模拟预测）如图，在矩形 SKIPIF 1 < 0 中，点 SKIPIF 1 < 0 在边 SKIPIF 1 < 0 上，且满足 SKIPIF 1 < 0 ，将 SKIPIF 1 < 0 沿 SKIPIF 1 < 0 向上翻折，使点 SKIPIF 1 < 0 到点 SKIPIF 1 < 0 的位置，构成四棱锥 SKIPIF 1 < 0 .
(1)若点 SKIPIF 1 < 0 在线段 SKIPIF 1 < 0 上，且 SKIPIF 1 < 0 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ，试确定点 SKIPIF 1 < 0 的位置；
(2)若 SKIPIF 1 < 0 ，求锐二面角 SKIPIF 1 < 0 的大小.
3-3、（2023·江苏南通·统考一模）如图，在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 是 SKIPIF 1 < 0 边上的高，以 SKIPIF 1 < 0 为折痕，将 SKIPIF 1 < 0 折至 SKIPIF 1 < 0 的位置，使得 SKIPIF 1 < 0 .
(1)证明： SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ；
(2)若 SKIPIF 1 < 0 ，求二面角 SKIPIF 1 < 0 的正弦值.
1、（2023·江苏南京·校考一模）中学开展劳动实习，学习加工制作食品包装盒.现有一张边长为6的正六边形硬纸片，如图所示，裁掉阴影部分，然后按虚线处折成高为 SKIPIF 1 < 0 的正六棱柱无盖包装盒，则此包装盒的体积为（ ）
A．144B．72C．36D．24
2、（2023·吉林·统考三模）如图，菱形纸片 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，O为菱形 SKIPIF 1 < 0 的中心，将纸片沿对角线 SKIPIF 1 < 0 折起，使得二面角 SKIPIF 1 < 0 为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 分别为 SKIPIF 1 < 0 的中点，则折纸后 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D．0
3、（2023·湖南邵阳·统考三模）如图所示，正八面体的棱长为2，则此正八面体的表面积与体积之比为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
4、（2023·河北唐山·统考三模）把边长为 SKIPIF 1 < 0 的正方形 SKIPIF 1 < 0 沿对角线 SKIPIF 1 < 0 折成直二面角 SKIPIF 1 < 0 ，则三棱锥 SKIPIF 1 < 0 的外接球的球心到平面 SKIPIF 1 < 0 的距离为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
5、（2023·黑龙江大庆·统考三模）（多选题）勒洛四面体是一个非常神奇的“四面体”，它能在两个平行平面间自由转动，并且始终保持与两平面都接触.勒洛四面体是以正四面体的四个顶点为球心，以正四面体的棱长为半径的四个球的相交部分围成的几何体，若用棱长为4的正四面体 SKIPIF 1 < 0 作勒洛四面体，如图，则下列说法正确的是（ ）
A．平面 SKIPIF 1 < 0 截勒洛四面体所得截面的面积为 SKIPIF 1 < 0
B．记勒洛四面体上以C，D为球心的两球球面交线为弧 SKIPIF 1 < 0 ，则其长度为 SKIPIF 1 < 0
C．该勒洛四面体表面上任意两点间距离的最大值为4
D．该勒洛四面体能够容纳的最大球的半径为 SKIPIF 1 < 0
6、（2023·河北唐山·统考三模）（多选题）《九章算术》是我国古代的数学名著，书中提到底面为长方形的屋状的楔体（图示的五面体 SKIPIF 1 < 0 ．底面长方形 SKIPIF 1 < 0 中 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，上棱长 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ，高（即 SKIPIF 1 < 0 到平面 SKIPIF 1 < 0 的距离）为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 是底面的中心，则（ ）
A． SKIPIF 1 < 0 SKIPIF 1 < 0 平面 SKIPIF 1 < 0
B．五面体 SKIPIF 1 < 0 的体积为5
C．四边形 SKIPIF 1 < 0 与四边形 SKIPIF 1 < 0 的面积和为定值 SKIPIF 1 < 0
D． SKIPIF 1 < 0 与 SKIPIF 1 < 0 的面积和的最小值为 SKIPIF 1 < 0
7、（2023·江苏泰州·泰州中学校考一模）已知直三棱柱 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 分别为棱 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的中点，过点 SKIPIF 1 < 0 作平面 SKIPIF 1 < 0 将此三棱柱分成两部分，其体积分别记为 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 __________；平面 SKIPIF 1 < 0 截此三棱柱的外接球的截面面积为__________．
8、（2023·吉林长春·统考三模）如图，平面五边形 SKIPIF 1 < 0 中，△ SKIPIF 1 < 0 是边长为2的等边三角形， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，将△ SKIPIF 1 < 0 沿 SKIPIF 1 < 0 翻折，使点 SKIPIF 1 < 0 翻折到点 SKIPIF 1 < 0 ．
(1)证明： SKIPIF 1 < 0 ；
(2)若 SKIPIF 1 < 0 ，求直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的正弦值．