新高考数学一轮复习 专项分层精练第07课 幂函数与二次函数（2份打包，原卷版+解析版）

这是一份新高考数学一轮复习 专项分层精练第07课 幂函数与二次函数（2份打包，原卷版+解析版），文件包含新高考数学一轮复习专项分层精练第07课幂函数与二次函数原卷版doc、新高考数学一轮复习专项分层精练第07课幂函数与二次函数解析版doc等2份试卷配套教学资源，其中试卷共40页， 欢迎下载使用。
一、单选题
1．（2022·全国·高一专题练习）若函数 SKIPIF 1 < 0 ，则函数 SKIPIF 1 < 0 的最小值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
2．（2022春·河南新乡·高二校考阶段练习）下列函数中，在 SKIPIF 1 < 0 上单调递减的是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
3．（2022春·陕西宝鸡·高一宝鸡市渭滨中学校考阶段练习）已知函数 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则（ ）
A．最大值为2，最小值为1
B．最大值为 SKIPIF 1 < 0 ，最小值为1
C．最大值为 SKIPIF 1 < 0 ，最小值为1
D．最大值为 SKIPIF 1 < 0 ，最小值为 SKIPIF 1 < 0
4．（2023·重庆酉阳·重庆市酉阳第一中学校校考一模）若函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上是单调减函数，则 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
5．（2023·江苏镇江·扬中市第二高级中学校考模拟预测）已知幂函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上是减函数，则 SKIPIF 1 < 0 的值为（ ）
A．3B． SKIPIF 1 < 0 C．1D． SKIPIF 1 < 0
6．（2023·全国·高三专题练习）已知幂函数 SKIPIF 1 < 0 的图象经过点 SKIPIF 1 < 0 与点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
7．（2023·河南信阳·信阳高中校考模拟预测）已知幂函数 SKIPIF 1 < 0 的图象过点 SKIPIF 1 < 0 ．设 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 的大小关系是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
8．（2021·河北衡水·河北衡水中学校考三模）已知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则实数 SKIPIF 1 < 0 的取值范围为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
9．（2022秋·江苏连云港·高一期末）已知幂函数 SKIPIF 1 < 0 的图象过函数 SKIPIF 1 < 0 的图象所经过的定点，则 SKIPIF 1 < 0 的值等于（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C．2D． SKIPIF 1 < 0
10．（2023·全国·高三专题练习）若幂函数 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ，则下列关于函数 SKIPIF 1 < 0 的判断正确的是（ ）
A． SKIPIF 1 < 0 是周期函数B． SKIPIF 1 < 0 是单调函数
C． SKIPIF 1 < 0 关于点 SKIPIF 1 < 0 对称D． SKIPIF 1 < 0 关于原点对称
11．（2023·四川南充·阆中中学校考二模）下列函数中，在 SKIPIF 1 < 0 上是增函数的是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
12．（2021春·陕西延安·高二子长市中学校考期末）幂函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 为增函数，则 SKIPIF 1 < 0 的值是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 或 SKIPIF 1 < 0 D． SKIPIF 1 < 0 或 SKIPIF 1 < 0
13．（2022·全国·高三专题练习）若 SKIPIF 1 < 0 则满足 SKIPIF 1 < 0 的x的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
14．（2023·广西·统考模拟预测）已知函数 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C．8D．9
二、多选题
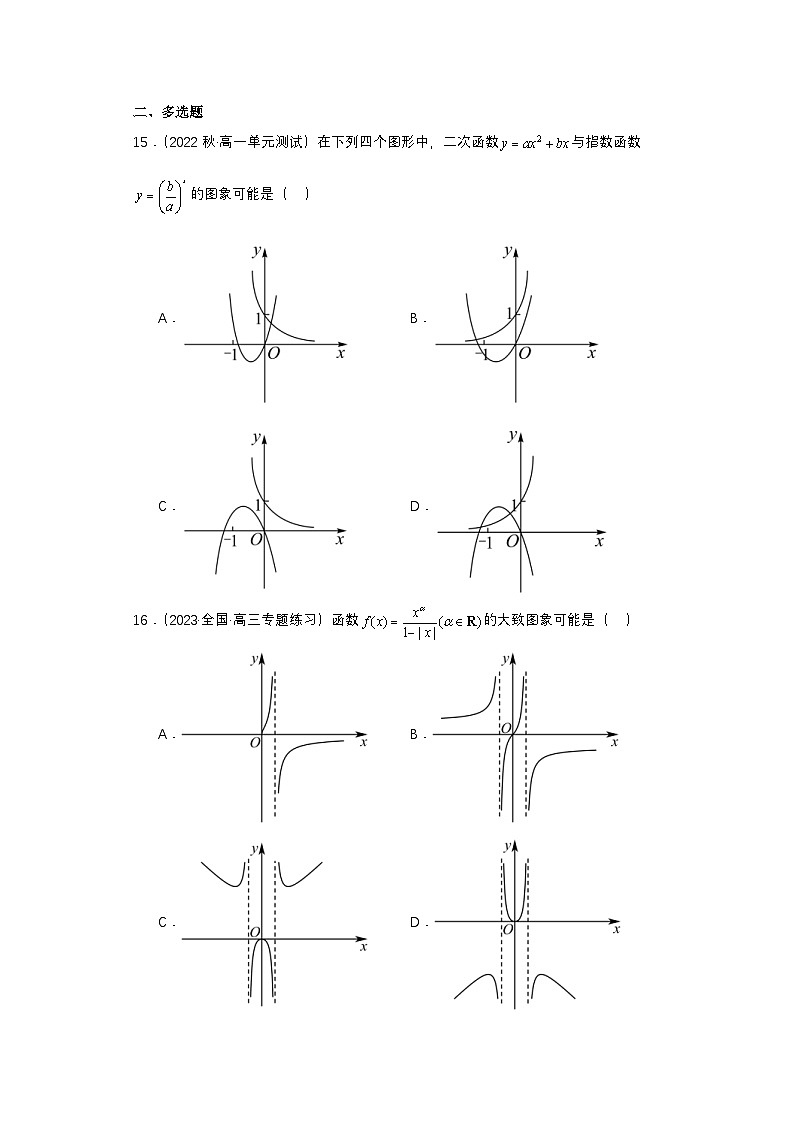
15．（2022秋·高一单元测试）在下列四个图形中，二次函数 SKIPIF 1 < 0 与指数函数 SKIPIF 1 < 0 的图象可能是（ ）
A．B．
C．D．
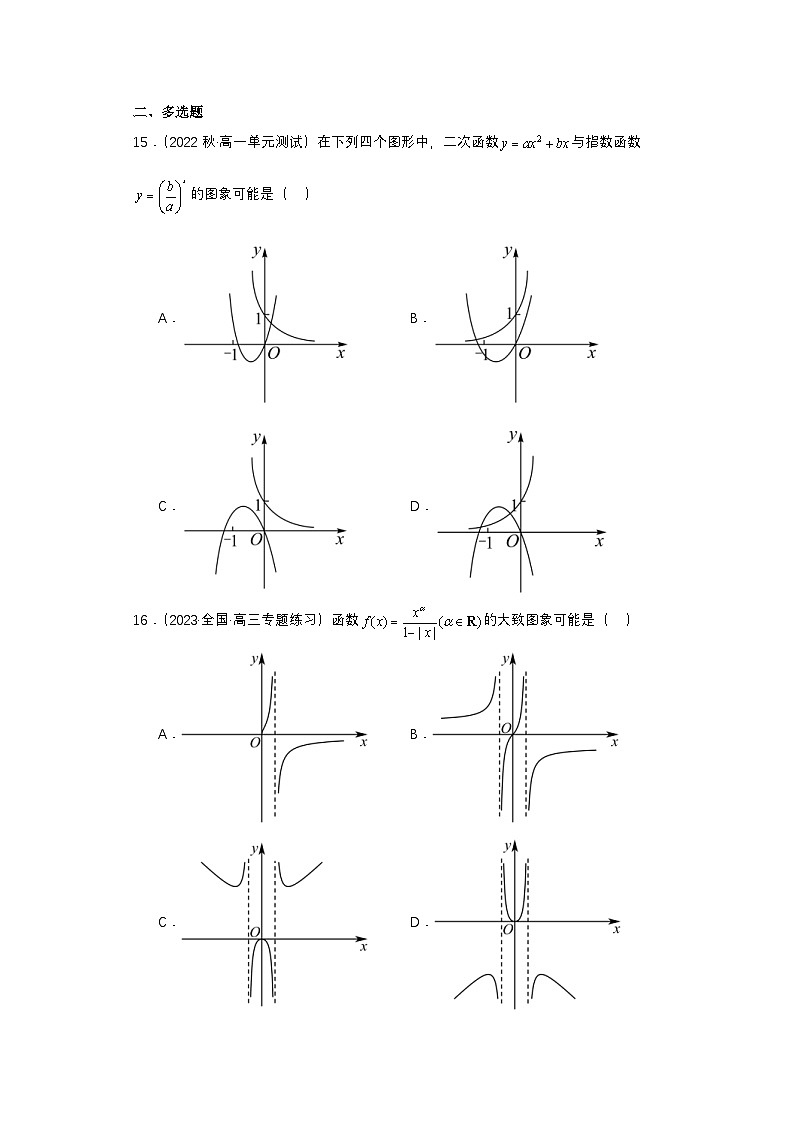
16．（2023·全国·高三专题练习）函数 SKIPIF 1 < 0 的大致图象可能是（ ）
A．B．
C．D．
三、填空题
17．（2012·江苏·高考真题）已知函数的值域为 SKIPIF 1 < 0 ，若关于x的不等式 SKIPIF 1 < 0 的解集为 SKIPIF 1 < 0 ，则实数c的值为 ．
18．（2020秋·广东阳江·高一阳江市第一中学校考阶段练习）如果二次函数 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上是减函数，那么 SKIPIF 1 < 0 的取值范围是 .
19．（2022秋·河南信阳·高一统考期中）函数 SKIPIF 1 < 0 是幂函数，且在 SKIPIF 1 < 0 上是减函数，则实数 SKIPIF 1 < 0 .
20．（2020秋·全国·高一专题练习）已知幂函数 SKIPIF 1 < 0 的图象关于 SKIPIF 1 < 0 轴对称，且在区间 SKIPIF 1 < 0 上为减函数，则 SKIPIF 1 < 0 的值为 ．
【二层练综合】
一、单选题
1．（2023·全国·高三专题练习）已知函数 SKIPIF 1 < 0 的值域为 SKIPIF 1 < 0 ，则实数 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
2．（2019·全国·高三专题练习）定义域为 SKIPIF 1 < 0 的函数 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ，且当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，则当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 的最小值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
3．（2023·全国·高一专题练习）函数 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 与函数 SKIPIF 1 < 0 在同一坐标系内的图象不可能的是（ ）
A．B．
C．D．
4．（2023·全国·高三专题练习）已知函数 SKIPIF 1 < 0 满足对任意的实数 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，都有 SKIPIF 1 < 0 成立，则实数 SKIPIF 1 < 0 的取值范围为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
5．（2023·全国·高三专题练习）已知二次函数 SKIPIF 1 < 0 的值域为 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的最小值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
6．（2022秋·宁夏中卫·高三中宁一中校考阶段练习）“幂函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上为增函数”是“函数 SKIPIF 1 < 0 为奇函数”的（ ）条件
A．充分不必要B．必要不充分
C．充分必要D．既不充分也不必要
7．（2023·广东东莞·校考模拟预测）已知函数 SKIPIF 1 < 0 （ SKIPIF 1 < 0 且 SKIPIF 1 < 0 ）的图象恒过定点 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 在幂函数 SKIPIF 1 < 0 的图象上，则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
8．（2022·全国·高三专题练习）已知定义在 SKIPIF 1 < 0 上的幂函数 SKIPIF 1 < 0 （ SKIPIF 1 < 0 为实数）过点 SKIPIF 1 < 0 ，记 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的大小关系为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
9．（2010·上海徐汇·统考高考模拟）下列函数中，与幂函数 SKIPIF 1 < 0 有相同定义域的是（ ）
A． SKIPIF 1 < 0 ；B． SKIPIF 1 < 0 ；C． SKIPIF 1 < 0 ；D． SKIPIF 1 < 0 ．
10．（2022秋·山西晋城·高三晋城市第一中学校校考阶段练习）若集合 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
11．（2023·四川·校联考模拟预测）已知 SKIPIF 1 < 0 与 SKIPIF 1 < 0 都是定义在 SKIPIF 1 < 0 上的函数， SKIPIF 1 < 0 是奇函数， SKIPIF 1 < 0 是偶函数，且 SKIPIF 1 < 0 ， SKIPIF 1 < 0 都不是常数函数，现有下列三个结论：① SKIPIF 1 < 0 ；② SKIPIF 1 < 0 的图象关于直线 SKIPIF 1 < 0 对称；③ SKIPIF 1 < 0 与 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上的单调性可能相同 SKIPIF 1 < 0 其中正确结论的个数为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
12．（2023春·四川成都·高一校联考期末）幂函数 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上单调递减，则下列说法正确的是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 是减函数
C． SKIPIF 1 < 0 是奇函数D． SKIPIF 1 < 0 是偶函数
二、多选题
13．（2020秋·安徽安庆·高一桐城市第八中学校考阶段练习）关于 SKIPIF 1 < 0 的方程 SKIPIF 1 < 0 ，下列命题正确的有（ ）
A．存在实数 SKIPIF 1 < 0 ，使得方程无实根
B．存在实数 SKIPIF 1 < 0 ，使得方程恰有2个不同的实根
C．存在实数 SKIPIF 1 < 0 ，使得方程恰有3个不同的实根
D．存在实数 SKIPIF 1 < 0 ，使得方程恰有4个不同的实根
14．（2023·全国·高三专题练习）已知 SKIPIF 1 < 0 ，则函数 SKIPIF 1 < 0 的图象可能是（ ）
A．B．
C．D．
15．（2023·江苏镇江·扬中市第二高级中学校考模拟预测）下列说法正确的是（ ）
A．函数 SKIPIF 1 < 0 的单调增区间为 SKIPIF 1 < 0
B．函数 SKIPIF 1 < 0 为奇函数
C．幂函数 SKIPIF 1 < 0 是减函数
D． SKIPIF 1 < 0 图像关于点 SKIPIF 1 < 0 成中心对称
16．（2023·全国·高三专题练习）若a＞b＞0＞c，则( )
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
三、填空题
17．（2023·辽宁葫芦岛·统考二模）已知函数 SKIPIF 1 < 0 ，则关于x的不等式 SKIPIF 1 < 0 的解集为 ．
18．（2022秋·湖南郴州·高一安仁县第一中学校考阶段练习）若幂函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上为增函数则 SKIPIF 1 < 0 ．
19．（2022·河南·校联考模拟预测）已知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，若对 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则实数 SKIPIF 1 < 0 的取值范围是 .
20．（2023·陕西榆林·校考模拟预测）直线 SKIPIF 1 < 0 ： SKIPIF 1 < 0 与 SKIPIF 1 < 0 ， SKIPIF 1 < 0 轴的交点分别是 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 与函数 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的图像的交点分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 是线段 SKIPIF 1 < 0 的三等分点，则 SKIPIF 1 < 0 的值为 .
21．（2017·四川绵阳·统考一模） SKIPIF 1 < 0 是定义在 SKIPIF 1 < 0 上的偶函数，且 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，若对任意的 SKIPIF 1 < 0 ，不等式 SKIPIF 1 < 0 恒成立，则实数 SKIPIF 1 < 0 的取值范围是 .
22．（2022·高一课时练习）已知 SKIPIF 1 < 0 .若函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上递减且为偶函数，则 SKIPIF 1 < 0 .
【三层练能力】
一、单选题
1．（2015·陕西·高考真题）对二次函数 SKIPIF 1 < 0 （ SKIPIF 1 < 0 为非零整数），四位同学分别给出下列结论，其中有且仅有一个结
论是错误的，则错误的结论是
A． SKIPIF 1 < 0 是 SKIPIF 1 < 0 的零点B．1是 SKIPIF 1 < 0 的极值点
C．3是 SKIPIF 1 < 0 的极值D．点 SKIPIF 1 < 0 在曲线 SKIPIF 1 < 0 上
2．（2022·全国·高三专题练习）已知幂函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递增，函数 SKIPIF 1 < 0 时，总存在 SKIPIF 1 < 0 使得 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
二、多选题
3．（2022秋·重庆·高三校联考阶段练习）在三角函数部分，我们研究过二倍角公式 SKIPIF 1 < 0 ，实际上类似的还有三倍角公式，则下列说法中正确的有（ ）
A． SKIPIF 1 < 0
B．存在 SKIPIF 1 < 0 时，使得 SKIPIF 1 < 0
C．给定正整数 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
D．设方程 SKIPIF 1 < 0 的三个实数根为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，并且 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
三、填空题
4．（2023·四川成都·校考一模）已知函数 SKIPIF 1 < 0 ，若存在 SKIPIF 1 < 0 ，使得 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的取值范围是 ．
5．（2023·全国·高三专题练习）关于x的不等式 SKIPIF 1 < 0 ，解集为
【一层练基础】参考答案
1．D
【分析】先利用配凑法求出 SKIPIF 1 < 0 的解析式，则可求出 SKIPIF 1 < 0 的解析式，从而可求出函数的最小值
【详解】因为 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 .
从而 SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 取得最小值，且最小值为 SKIPIF 1 < 0 .
故选：D
2．D
【分析】根据函数单调性的性质可判断每个选项中函数在 SKIPIF 1 < 0 的单调性.
【详解】对于A，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 单调递增，故A错误；
对于B， SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 在 SKIPIF 1 < 0 和 SKIPIF 1 < 0 上单调递增，故B错误；
对于C， SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递增，故C错误；
对于D， SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递减，故D正确
故选：D.
【点睛】本题主要考查对函数单调性的判断，根据基本初等函数的复合函数单调性进行判断即可，属于基础题.
3．B
【分析】利用 SKIPIF 1 < 0 化简f(x)解析式，根据二次函数的性质即可求f(x)最值.
【详解】 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 时，sinx∈[ SKIPIF 1 < 0 ，1]，
∴当sinx＝ SKIPIF 1 < 0 时，f(x)最大值为 SKIPIF 1 < 0 ；当sinx＝1时，f(x)最小值为1.
故选：B.
4．A
【分析】由求导公式和法则求出 SKIPIF 1 < 0 ，由导数与函数单调性的关系，列出不等式进行分离常数，再构造函数后，利用整体思想和二次函数的性质求出函数的最值，可得a的取值范围．
【详解】由题意得， SKIPIF 1 < 0 SKIPIF 1 < 0 ，
因为 SKIPIF 1 < 0 在[1，+∞）上是单调减函数，
所以 SKIPIF 1 < 0 ≤0在[1，+∞）上恒成立，
当 SKIPIF 1 < 0 ≤0时，则 SKIPIF 1 < 0 在[1，+∞）上恒成立，
即a SKIPIF 1 < 0 ，设g（x） SKIPIF 1 < 0 ，
因为x∈[1，+∞），所以 SKIPIF 1 < 0 ∈（0，1]，
当 SKIPIF 1 < 0 时，g（x）取到最大值是： SKIPIF 1 < 0 ，
所以a SKIPIF 1 < 0 ，
所以数a的取值范围是（﹣∞， SKIPIF 1 < 0 ]
故选：A
【点睛】关键点点睛：根据求导公式和法则，导数与函数单调性的关系，将问题转化为恒成立问题，利用分离常数法，求函数值域，属于中档题．
5．C
【分析】先根据 SKIPIF 1 < 0 是幂函数，由 SKIPIF 1 < 0 求得 SKIPIF 1 < 0 ，再根据函数在 SKIPIF 1 < 0 上是减函数，确定 SKIPIF 1 < 0 的值求解.
【详解】由函数 SKIPIF 1 < 0 为幂函数知，
SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 .
∵ SKIPIF 1 < 0 在 SKIPIF 1 < 0 上是减函数，而当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，在 SKIPIF 1 < 0 是增函数，不符合题意，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，符合题意，
∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 .
故选：C.
6．B
【分析】设幂函数 SKIPIF 1 < 0 ，依次将点 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 坐标代入，可得 SKIPIF 1 < 0 ，结合指数函数和对数函数性质即可得到答案.
【详解】设幂函数 SKIPIF 1 < 0 ，因为点 SKIPIF 1 < 0 在 SKIPIF 1 < 0 的图象上，
所以 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
又点 SKIPIF 1 < 0 在 SKIPIF 1 < 0 的图象上，所以 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
故选：B
7．D
【分析】根据幂函数的定义求出函数 SKIPIF 1 < 0 解析式，再利用幂函数的单调性比较大小而得解.
【详解】因幂函数 SKIPIF 1 < 0 的图象过点 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，
于是得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，函数 SKIPIF 1 < 0 ，函数 SKIPIF 1 < 0 是R上的增函数，
而 SKIPIF 1 < 0 ，则有 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 .
故选：D
8．A
【分析】根据指对幂不等式，结合指对幂函数的性质分别求参数a的范围，再取交集即可.
【详解】由 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，
由 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ，
由 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ，
∴当 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 同时成立时，取交集得 SKIPIF 1 < 0 ，
故选：A.
9．B
【分析】先根据幂函数定义得 SKIPIF 1 < 0 ，再确定 SKIPIF 1 < 0 的图像所经过的定点为 SKIPIF 1 < 0 ，代入 SKIPIF 1 < 0 解得 SKIPIF 1 < 0 的值.
【详解】由于 SKIPIF 1 < 0 为幂函数，则 SKIPIF 1 < 0 ，解得： SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ；
函数 SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，
故 SKIPIF 1 < 0 的图像所经过的定点为 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，解得： SKIPIF 1 < 0 ,
故选：B.
10．C
【分析】由题意得 SKIPIF 1 < 0 ，利用导数求出方程的根，进而可求出结果.
【详解】由题意得 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 ，
令 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 单调递减；当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 单调递增；所以 SKIPIF 1 < 0 ，因此方程 SKIPIF 1 < 0 有唯一解，解为 SKIPIF 1 < 0 ，因此 SKIPIF 1 < 0 ，所以不是周期函数，不是单调函数，关于点 SKIPIF 1 < 0 对称，
故选：C.
11．C
【解析】对AB：直接判断其单调性；
对C：把 SKIPIF 1 < 0 化为 SKIPIF 1 < 0 ，判断其单调性；
对D：利用 SKIPIF 1 < 0 判断 SKIPIF 1 < 0 的单调性.
【详解】本题考查函数的单调性.
A项中，函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递减，故A错误；
B项中，二次函数 SKIPIF 1 < 0 的图像开口向下，对称轴方程为 SKIPIF 1 < 0 ，故该函数在 SKIPIF 1 < 0 上单调递增，在 SKIPIF 1 < 0 上单调递减，故B错误；
C项中，函数 SKIPIF 1 < 0 ，在 SKIPIF 1 < 0 和 SKIPIF 1 < 0 上分别单调递增，故C正确；
D项中，函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递减，故D错误.
故选：C
【点睛】方法点睛：四个选项互不相关的选择题，需要对各个选项一一验证.
12．B
【分析】由幂函数解析式的形式可构造方程求得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，分别验证两种情况下 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上的单调性即可得到结果.
【详解】 SKIPIF 1 < 0 为幂函数， SKIPIF 1 < 0 ，解得： SKIPIF 1 < 0 或 SKIPIF 1 < 0 ；
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上为减函数，不合题意；
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上为增函数，符合题意；
综上所述： SKIPIF 1 < 0 .
故选：B.
13．B
【分析】按 SKIPIF 1 < 0 或0， SKIPIF 1 < 0 ， SKIPIF 1 < 0 和 SKIPIF 1 < 0 四种情况，分别化简解出不等式，可得x的取值范围．
【详解】①当 SKIPIF 1 < 0 或0时， SKIPIF 1 < 0 成立；
②当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，可有 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ；
③当 SKIPIF 1 < 0 且 SKIPIF 1 < 0 时， SKIPIF 1 < 0
若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0
若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0
所以 SKIPIF 1 < 0
则原不等式的解为 SKIPIF 1 < 0 ，
故选：B
14．C
【分析】利用诱导公式化简函数的表达式，利用三角函数和特殊幂函数的奇偶性进行分析，可得到 SKIPIF 1 < 0 ，进而计算得到答案.
【详解】由 SKIPIF 1 < 0 ，有 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 .
故选：C
15．ABD
【分析】根据 SKIPIF 1 < 0 的关系与各图形一个个检验即可判断．
【详解】当 SKIPIF 1 < 0 时，A正确；当 SKIPIF 1 < 0 时，B正确；
当 SKIPIF 1 < 0 时，D正确；当 SKIPIF 1 < 0 时，无此选项．
故选：ABD．
16．ABD
【分析】先根据当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ， SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，排除C，再举出适当的 SKIPIF 1 < 0 的值，分别得到ABD三个图象.
【详解】由题意知 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 的大致图象不可能为C，
而当 SKIPIF 1 < 0 为其他值时，A，B，D均有可能出现，
不妨设 SKIPIF 1 < 0 ，定义域为 SKIPIF 1 < 0 ，此时A选项符合要求；
当 SKIPIF 1 < 0 时，定义域为 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，
故函数 SKIPIF 1 < 0 为奇函数，所以B选项符合要求，
当 SKIPIF 1 < 0 时，定义域为 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，
故函数 SKIPIF 1 < 0 为偶函数，所以D选项符合要求.
故选：ABD
17．9．
【详解】∵f(x)＝x2＋ax＋b的值域为[0，＋∞)，∴Δ＝0，
∴b－ SKIPIF 1 < 0 ＝0，∴f(x)＝x2＋ax＋ SKIPIF 1 < 0 a2＝ SKIPIF 1 < 0 2.
又∵f(x)＜c的解集为(m，m＋6)，
∴m，m＋6是方程x2＋ax＋ SKIPIF 1 < 0 －c＝0的两根．由一元二次方程根与系数的关系得 SKIPIF 1 < 0 解得c＝9.
18． SKIPIF 1 < 0
【详解】 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上是减函数，则 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 .
19．2
【分析】根据函数为幂函数求参数m，讨论所求得的m判断函数是否在 SKIPIF 1 < 0 上是减函数，即可确定m值.
【详解】由题设， SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，此时函数在 SKIPIF 1 < 0 上递增，不合题意；
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，此时函数在 SKIPIF 1 < 0 上递减，符合题设.
综上， SKIPIF 1 < 0 .
故答案为：2
20．2
【分析】由幂指数为偶数且小于可得.
【详解】 SKIPIF 1 < 0 为偶数，且小于0，即 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，验证得 SKIPIF 1 < 0 ．
【点睛】幂函数 SKIPIF 1 < 0 中，当 SKIPIF 1 < 0 为奇数时，函数为奇函数，当 SKIPIF 1 < 0 为偶数时，函数为偶函数；当 SKIPIF 1 < 0 时，在第一象限内函数为增函数，当 SKIPIF 1 < 0 时，在第一象限内函数为减函数.
【二层练综合】参考答案
1．D
【分析】求出函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 时值的集合， 函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 时值的集合，再由已知并借助集合包含关系即可作答.
【详解】当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递增， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上值的集合是 SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递减，在 SKIPIF 1 < 0 上单调递增，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上值的集合为 SKIPIF 1 < 0 ，
因函数 SKIPIF 1 < 0 的值域为 SKIPIF 1 < 0 ，于是得 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，
所以实数 SKIPIF 1 < 0 的取值范围是 SKIPIF 1 < 0 .
故选：D
2．A
【分析】求出函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上的解析式，利用二次函数的基本性质可求得函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上的最小值.
【详解】当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，
由题意可得 SKIPIF 1 < 0 ，
所以，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 .
故选：A.
3．D
【分析】利用对数函数及二次函数的性质逐项分析即得.
【详解】对于A，由对数函数图象可知 SKIPIF 1 < 0 ，又函数 SKIPIF 1 < 0 ，对称轴为 SKIPIF 1 < 0