




2024年上海市虹口区五校中考联考数学试题(原卷版+解析版)
展开考生注意:
1.带2B铅笔、黑色签字笔、橡皮擦等参加考试,考试中途不得传借文具
2.不携带具有传送功能的通讯设备,一经发现视为作弊.与考试无关的所有物品放置在考场外.
3.考试开始15分钟后禁止入场,不得提前交卷,考试期间严格遵守考试纪律,诚信应考,杜绝作弊.
4.答题卡务必保持干净整洁,答题卡客观题建议检查好后再填涂.若因填涂模糊导致无法识别的后果自负.
5.本卷为回忆版,如有题目不同请联系,答案在本卷最后
一.选择题(共6题,每题4分,满分24分)
1. 下列计算正确的是( )
A. B. C. D.
2. 若关于x的不等式组无解,则a的取值范围是( )
A. a≤1B. a>1C. 1<a≤2D. ﹣1<a<1
3. 下列平面直角坐标系内的曲线中,既是中心对称图形,也是轴对称图形的是( )
A. 三叶玫瑰线B. 四叶玫瑰线
C. 心形线D. 笛卡尔叶形线
4. 下列说法中,不正确的是
A. 等腰三角形底边上的中线就是它的顶角平分线
B. 等腰三角形底边上的高就是底边的垂直平分线的一部分
C. 一条线段可看作以它的垂直平分线为对称轴的轴对称图形
D. 两个三角形能够重合,它们一定是轴对称的
5. 知直线,直线,且,若以中的一条直线为x轴,中的一条直线为y轴,建立平面直角坐标系,设向右、向上为正方向,且抛物线与这四条直线的位置如图所示,则所建立的平面直角坐标系中的x轴、y轴分别为( )
A. 直线B. 直线C. 直线D. 直线
6. 某部影片的盈利额(即影片的票房收入与固定成本之差)记为y,观影人数记为x,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后y与x的函数图象.
给出下列四种说法:
①图(2)对应的方案是:提高票价,并提高成本;
②图(2)对应的方案是:保持票价不变,并降低成本;
③图(3)对应的方案是:提高票价,并保持成本不变:
④图(3)对应的方案是:提高票价,并降低成本.
其中,正确的说法是( )
A. ①③B. ①④C. ②③D. ②④
二.填空题(共12题,每题4分,满分48分)
7. 因式分解:________.
8. 已知,则的值为_____.
9. 函数的定义域为_______.
10. 不等式的解集为_________.
11. 在某公司的面试中,李明的得分情况为:个人形象85分,工作能力90分,交际能力80分,已知个人形象、工作能力和交际能力的权重为1: 2: 2,则李明的最终成绩是_____________.
12. 已知反比例函数的图象与直线交于点,则这个反比例函数的解析式为______.
13. 正六边形的中心角等于______度.
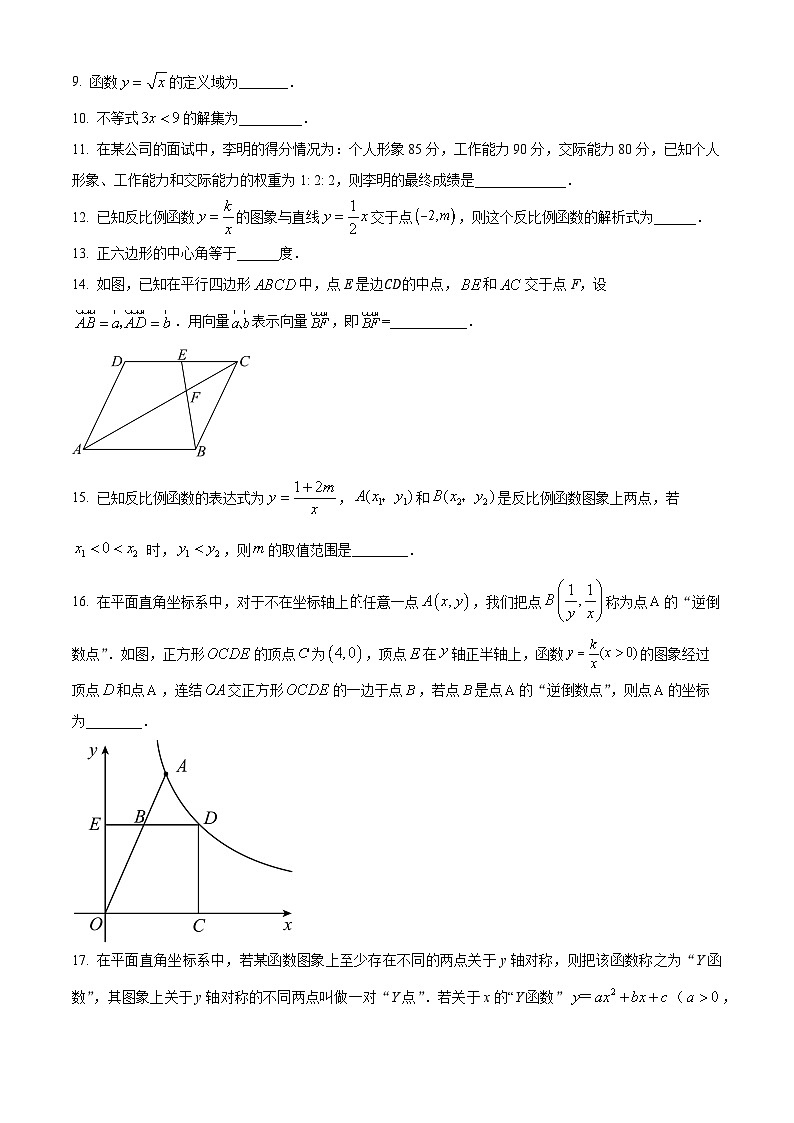
14. 如图,已知在平行四边形中,点E是边CD的中点,和交于点F,设.用向量表示向量,即=___________.
15. 已知反比例函数的表达式为,和是反比例函数图象上两点,若 时,,则的取值范围是________.
16. 在平面直角坐标系中,对于不在坐标轴上任意一点,我们把点称为点的“逆倒数点”.如图,正方形的顶点为,顶点在轴正半轴上,函数的图象经过顶点和点,连结交正方形的一边于点,若点是点的“逆倒数点”,则点的坐标为________.
17. 在平面直角坐标系中,若某函数图象上至少存在不同的两点关于y轴对称,则把该函数称之为“Y函数”,其图象上关于y轴对称的不同两点叫做一对“Y点”.若关于x的“Y函数”(,且a,b,c是常数)经过坐标原点O,且与直线l:(,且m,n是常数)交于两点,当满足时,则直线l经过的定点为 _____.
18. 如图,在矩形中,,是的中点,连接是边AD上一动点,过点的直线将矩形折叠,使点落在上的处,当是以为腰的等腰三角形时,_______.
三.解答题(满分78分)
19 计算:.
20. 解方程组:
21. 如图1是一张乒乓球桌,其侧面简化结构如图2所示,台面(台面厚度忽略不计)与地面平行,且高度为(台面与地面之间的距离),直线型支架与的上端E,F与台面下方相连,与的下端P,Q与直径为的脚轮(侧面是圆)相连(衔接之间的距离忽略不计),直线型支架与的上端C,D与台面下方相连,下端G,H与,相连,圆弧形支架分别与,在点G,H相连,且,已知,,
(1)求:的长度
(2)当所在的圆经过点P、Q时,求:所在的圆的圆心到台面之间的距离
22. “长度”和“角度”是几何学研究的核心问题.相交线与平行线的学习,让我们对“角度转化”有了深刻的体会.某数学兴趣小组受此启发,试图沟通“角度”与“长度”间的关系.在研究过程中他们发现了一条关于三角形的重要结论----“等角对等边”,即:如果一个三角形有两个角相等,那么这两个角所对的边也相等.
如右图,在中,若,则.
以此为基础,该兴趣小组邀请你加入研究,继续解决如下新问题:
在平面直角坐标系中,,,已知,点为轴上方一点.
(1)如图1,若的角平分线交于点,已知点,上有一点.则①与轴的位置关系为______;②求的长度;
(2)如图2,、分别平分、,过点作的平行线,分别交、于点、.若,,求四边形的周长;
(3)当点为轴上方的一动点(不在轴上)时,连接、.若邻补角的角平分线和的角平分线交于点,过点作的平行线,分别交直线、直线于点、.随着点移动,图形形状及点、、的位置也跟着变化,但线段、和之间却总是存在着确定的数量关系,请直接写出这三条线段之间的数量关系______.
23. 如图,在菱形中,,连结,E,F分别是,上的点,且,连接,交于点P.
(1)求证:;
(2)连结交于O点,设,,求证:
24. 二次函数的图象交x轴于点,点,交轴于点,抛物线的顶点为点.
(1)求二次函数的解析式;
(2)如图1,点是抛物线上的一点,设点P的横坐标为,点在对称轴上,且,若,请求出的值;
(3)如图2,将抛物线绕轴正半轴上一点旋转得到新抛物线交轴于,两点,点的对应点为点,点B的对应点为点.若,求旋转中心点的坐标
25. 如果三角形两个内角与满足,那么我们称这样的三角形为“准互余三角形”.
(1)若“准互余三角形”,,则________.
(2)如图(1),是半圆的直径,是半圆上的点,D是上的点,交于点E.
①若D是的中点,则图中共有_______个“准互余三角形”;
②当是“准互余三角形”时,求的长;
③如图(2)所示,若F是上的点(不与B、C重合),G为射线上一点,且满足.当是“准互余三角形”时,求的长.
精品解析:2024年福建省百校联考中考三模数学试题(原卷版+解析版): 这是一份精品解析:2024年福建省百校联考中考三模数学试题(原卷版+解析版),文件包含精品解析2024年福建省百校联考中考三模数学试题原卷版docx、精品解析2024年福建省百校联考中考三模数学试题解析版docx等2份试卷配套教学资源,其中试卷共34页, 欢迎下载使用。
2024年陕西省西安市莲湖区五校联考中考模拟数学试题(原卷版+解析版): 这是一份2024年陕西省西安市莲湖区五校联考中考模拟数学试题(原卷版+解析版),文件包含2024年陕西省西安市莲湖区五校联考中考模拟数学试题原卷版docx、2024年陕西省西安市莲湖区五校联考中考模拟数学试题解析版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。
2024年安徽省合肥省十校中考联考数学试题(原卷版+解析版): 这是一份2024年安徽省合肥省十校中考联考数学试题(原卷版+解析版),文件包含2024年安徽省合肥省十校中考联考数学试题原卷版docx、2024年安徽省合肥省十校中考联考数学试题解析版docx等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。












