




2024-2025学年第一学期人教版九年级数学期中模拟训练卷(解析版)
展开一、选择题:本题共10题,每题3分,共30分.每小题只有一个选项符合题目要求.
1.下列既是轴对称图形,又是中心对称图形的是( )
A.B.C.D.
2.点M(4,-3)关于原点对称的点N的坐标是( )
A.(-4,-3)B.(-4,3)C.(4,3)D.(-3,4)
3.由平移得到抛物线,则下列平移过程正确的是( )
A.先向左平移1个单位,再向上平移2个单位
B.先向左平移1个单位,再向下平移2个单位
C.先向右平移1个单位,再向下平移2个单位
D.先向右平移1个单位,再向上平移2个单位
4.已知,则( )
A.B.C.D.
5. 抛物线与y轴的交点坐标为( )
A.B.C.D.
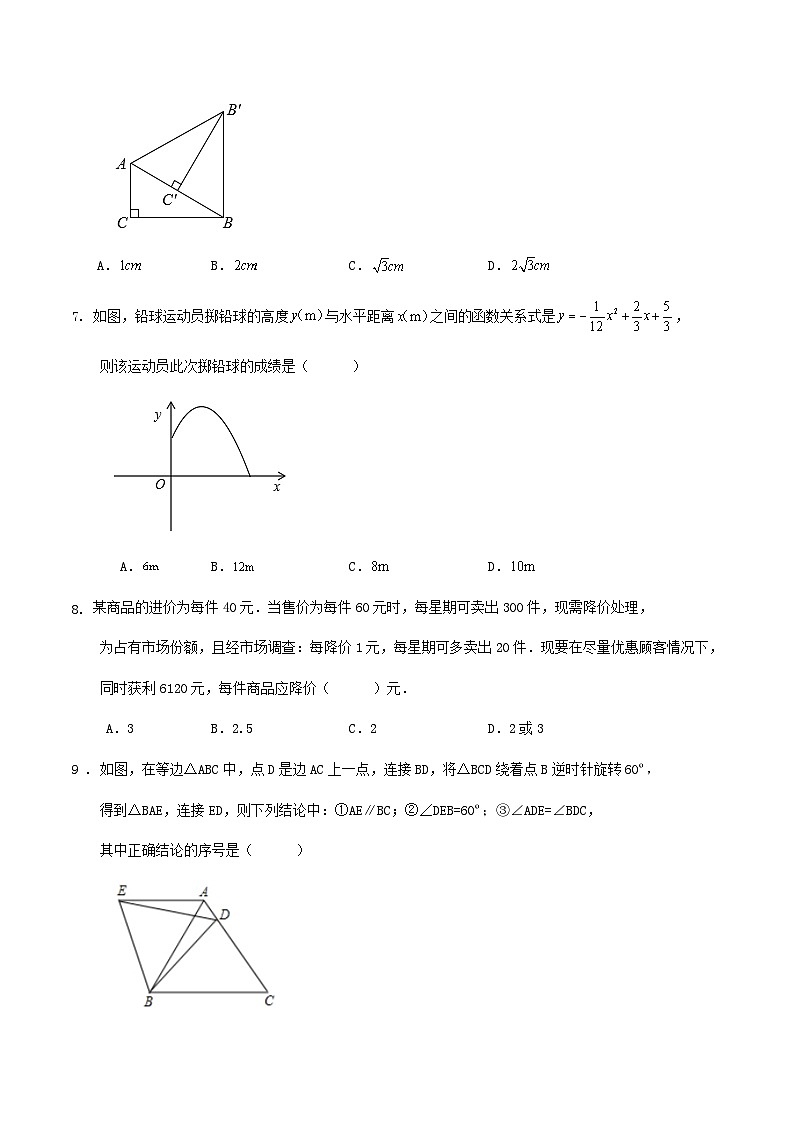
6 .如图,在中,将绕点逆时针旋转得到,
使点落在边上,连接,则的长度是( )
A.B.C.D.
7. 如图,铅球运动员掷铅球的高度与水平距离之间的函数关系式是,
则该运动员此次掷铅球的成绩是( )
A.B.C.D.
某商品的进价为每件40元.当售价为每件60元时,每星期可卖出300件,现需降价处理,
为占有市场份额,且经市场调查:每降价1元,每星期可多卖出20件.现要在尽量优惠顾客情况下,
同时获利6120元,每件商品应降价( )元.
A.3B.2.5C.2D.2或3
9 . 如图,在等边△ABC中,点D是边AC上一点,连接BD,将△BCD绕着点B逆时针旋转60º,
得到△BAE,连接ED,则下列结论中:①AE∥BC;②∠DEB=60º;③∠ADE=∠BDC,
其中正确结论的序号是( )
A.①②B.①③C.②③D.只有①
10.二次函数的图象如图所示,下列结论:
①;②;③;④当时,随的增大而减小.
其中结论正确的有( )
A.4个B.3个C.2个D.1个
二、填空题:本大题共8个小题.每小题3分,共24分.把答案填在题中横线上.
11.已知点与点关于原点O对称,则 .
12.设m是方程的一个根,则的值为 .
如图,△ABC中,∠C=30°.将△ABC绕点A顺时针旋转60°得到△ADE,AE与BC交于F,
则∠AFB= °.
14.若关于x的方程x2+5x+m=0的两个根分别为为x1,x2,且=1,则m= .
15.抛物线与轴的一个交点为,则另一个交点坐标为 .
16.美术兴趣小组在中秋节这一天人人相互送一个月饼,共送出56个月饼,美术兴趣小组人数是______
已知二次函数的图象如图所示,下列结论:
①,②,③,④,其中正确的是 .
如图,在中,,将绕点A逆时针旋转得到,
连接,则下列结论:①,②,③,④,
其中正确的是_____________(填序号)
三、解答题:(本大题共8个小题,共66分,解答应写出文字说明、证明过程或演算步骤)
19.用适当的方法解方程:
(1);
(2).
20.ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.按要求作图:
(1)画出△ABC关于原点O的中心对称图形△A1B1C1.
(2)将△ABC绕点A逆时针旋转90°得到△A2B2C2,则B2的坐标为 .
(3)求△A2B2C2面积.
21.已知关于x的方程.
(1)若此方程的一个根为1,求m的值;
(2)求证:不论m取何实数,此方程都有两个不相等的实数根.
22 如图,点O是等边ABC内一点,将CO绕点C顺时针旋转60°得到CD,连接OD,AO,BO,AD.
(1)求证:BCO≌ACD.
(2)若OA=10,OB=8,OC=6,求∠BOC的度数.
23.阅读下列材料
解方程:.这是一个一元四次方程,根据该方程的特点,
它的解法通常是:
设,那么,于是原方程可变为…①,
解这个方程得:.
当时,.∴;
当时,,∴
所以原方程有四个根: .
在这个过程中,我们利用换元法达到降次的目的,体现了转化的数学思想.
(1)解方程时,若设,求出x.
(2)利用换元法解方程.
某化工材料经销公司购进一种化工原料若干千克,价格为每千克30元,
物价部门规定其销售单价不高于每千克70元,不低于每千克30元,经市场调查发现:
目前销量y(千克)是销售单价x(元)的一次函数,且当时,,时,,
在销售过程中,每天还要支付其他费用450元.
(1)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式.
(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元.
25.综合与实践
问题情境:如图1,在中,,,,点在直线上运动,以为边作,使得,,.连接.当点在边上时,试判断线段,及之间的数量关系.
探究展示:勤奋小组发现,,并展示了如下论述过程:
理由如下:∵在和中,,,
.
∴,即.
在与中,
∴(依据1).
∴(依据2)
∵,∴.
反思交流:
(1)上述证明过程中的“依据1”,“依据2”分别是什么?
(2)如图2,缜密小组在勤奋小组的基础上继续探究,当点在延长线上时,
线段,及之间的数量关系是,且与的位置关系是;
请判断缜密小组的说法是否正确,若正确,请说明理由;
若不正确,请把你发现的结果写出并说明理由;
如图3,当点D在边BC的延长线上且其他条件不变时,(2)中BC,CE,CD之间存在的关系是否成立?
如不成立,请直接写出BC,CE,CD之间存在的数量关系,并证明.
26.如图1,抛物线与x轴交于点A、B4,0(A点在B点左侧),与y轴交于点C0,6,点P是抛物线上一个动点,连接,,
(1)求抛物线的函数表达式;
(2)若点P的横坐标为3,求的面积;
(3)如图2所示,当点P在直线上方运动时,连接,求四边形面积的最大值,
并写出此时P点坐标.
若点M是轴上的一个动点,点N是抛物线上一动点,P的横坐标为3.试判断是否存在这样的点M,
使得以点B,M,N,P为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;
若不存在,请说明理由.
2024-2025学年九年级上学期开学数学摸底卷(人教版)(解析版): 这是一份2024-2025学年九年级上学期开学数学摸底卷(人教版)(解析版),共20页。
2023-2024学年第一学期杭州市九年级期中数学复习卷(解析版): 这是一份2023-2024学年第一学期杭州市九年级期中数学复习卷(解析版),文件包含2023-2024学年第一学期杭州市九年级期中数学复习卷解析版docx、2023-2024学年第一学期杭州市九年级期中数学复习卷docx等2份试卷配套教学资源,其中试卷共35页, 欢迎下载使用。
2024-2025学年第一学期人教版九年级数学期中模拟预测试卷(解析版): 这是一份2024-2025学年第一学期人教版九年级数学期中模拟预测试卷(解析版),文件包含2024-2025学年第一学期人教版九年级数学期中模拟预测试卷解析版docx、2024-2025学年第一学期人教版九年级数学期中模拟预测试卷docx等2份试卷配套教学资源,其中试卷共35页, 欢迎下载使用。












