第七章　§7.9　立体几何中的截面、交线问题-2025年新高考数学一轮复习（课件+讲义+练习）

这是一份第七章　§7.9　立体几何中的截面、交线问题-2025年新高考数学一轮复习（课件+讲义+练习），文件包含第七章§79立体几何中的截面交线问题pptx、第七章§79立体几何中的截面交线问题教师版docx、第七章§79立体几何中的截面交线问题同步练习docx、第七章§79立体几何中的截面交线问题-2025新高考一轮复习讲义学生版docx等4份课件配套教学资源，其中PPT共48页， 欢迎下载使用。

1、揣摩例题。课本上和老师讲解的例题，一般都具有一定的典型性和代表性。要认真研究，深刻理解，要透过“样板”，学会通过逻辑思维，灵活运用所学知识去分析问题和解决问题，特别是要学习分析问题的思路、解决问题的方法，并能总结出解题的规律。 2、精练习题。复习时不要搞“题海战术”，应在老师的指导下，选一些源于课本的变式题，或体现基本概念、基本方法的基本题，通过解题来提高思维能力和解题技巧，加深对所学知识的深入理解。在解题时，要独立思考，一题多思，一题多解，反复玩味，悟出道理。 3、加强审题的规范性。每每大考过后，总有同学抱怨没考好，纠其原因是考试时没有注意审题。审题决定了成功与否，不解决这个问题势必影响到高考的成败。那么怎么审题呢? 应找出题目中的已知条件 ;善于挖掘题目中的隐含条件 ;认真分析条件与目标的联系，确定解题思路 。 4、重视错题。“错误是最好的老师”，但更重要的是寻找错因，及时进行总结，三五个字，一两句话都行，言简意赅，切中要害，以利于吸取教训，力求相同的错误不犯第二次。
§7.9　立体几何中的截面、交线问题
“截面、交线”问题是高考立体几何问题中最具创新意识的题型，它渗透了一些动态的线、面等元素，给静态的立体几何题赋予了活力.求截面、交线问题，一是与解三角形、多边形面积、周长、扇形弧长、面积等相结合求解，二是利用空间向量的坐标运算求解.
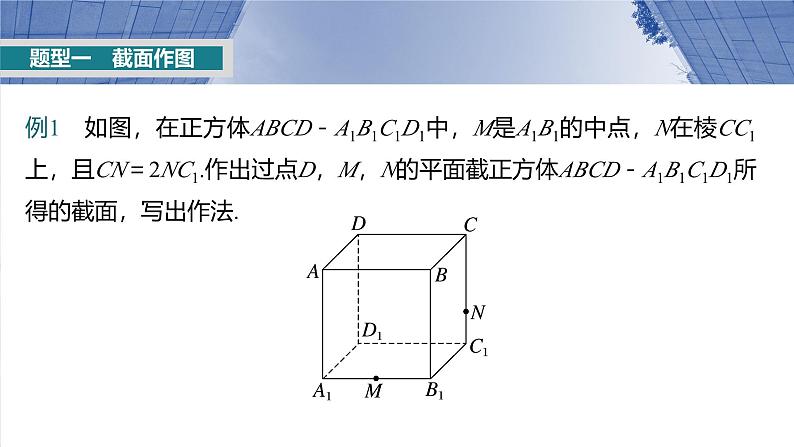
例1　如图，在正方体ABCD－A1B1C1D1中，M是A1B1的中点，N在棱CC1上，且CN＝2NC1.作出过点D，M，N的平面截正方体ABCD－A1B1C1D1所得的截面，写出作法.
如图所示，五边形DQMFN即为所求截面.作法如下：连接DN并延长交D1C1的延长线于点E，连接ME交B1C1于点F，交D1A1的延长线于点H，连接DH交AA1于点Q，连接QM，FN，则五边形DQMFN即为所求截面.
作截面的几种方法(1)直接法：有两点在几何体的同一个面上，连接该两点即为几何体与截面的交线，找截面实际就是找交线的过程.(2)延长线法：同一个平面有两个点，可以连线并延长至与其他平面相交找到交点.(3)平行线法：过直线与直线外一点作截面，若直线所在的面与点所在的平面平行，可以通过过点找直线的平行线找到几何体与截面的交线.
跟踪训练1　如图，已知在正方体ABCD－A1B1C1D1中，M是棱AA1的中点，过C，D1，M三点作正方体的截面，作出这个截面图，写出作法.
如图，连接CD1，连接D1M并延长，交DA的延长线于点N，连接CN交AB于点P，连接MP，则四边形CD1MP为过C，D1，M三点的正方体的截面.
例2　(多选)在正方体ABCD－A1B1C1D1中，点E是线段DD1上的动点，若过A，B1，E三点的平面将正方体截为两个部分，则所得截面的形状可能为A.等边三角形 B.矩形C.菱形 D.等腰梯形
题型二　截面图形的形状判断
当点E与D1重合时，过A，B1，E三点的截面是等边三角形AB1D1，故A正确；当点E与D重合时，过A，B1，E三点的截面为矩形AB1C1D，故B正确；若截面为菱形，则必有AB1＝AE，此时点E与D1重合，故C错误；当点E与DD1中点重合时，记C1D1的中点为F，连接EF，FB1，C1D(图略)，易知EF∥DC1，由正方体性质可知，AD∥B1C1且AD＝B1C1，
所以四边形AB1C1D为平行四边形，所以DC1∥AB1，
所以过A，B1，E三点的截面为等腰梯形AB1FE，故D正确.
判断几何体被一个平面所截的截面形状，关键在于弄清这个平面与几何体的面相交成线的形状和位置.
跟踪训练2　已知一个棱柱的底面是正六边形，侧面都是正方形，用至少过该棱柱三个顶点(不在同一侧面或同一底面内)的平面去截这个棱柱，所得截面的形状不可能是A.等腰三角形 B.等腰梯形C.五边形 D.正六边形
如图①，由图可知，截面ABC为等腰三角形，选项A可能；截面ABEF为等腰梯形，选项B可能；如图②，截面AMDEN为五边形，选项C可能；
因为侧面是正方形，只有平行于底面的截面才可能是正六边形，故过两底的顶点不可能得到正六边形，选项D不可能.
例3　(2024·朔州模拟)在正方体ABCD－A1B1C1D1中，棱长为3，E为棱BB1上靠近B1的三等分点，则平面AED1截正方体ABCD－A1B1C1D1的截面面积为
题型三　截面图形的周长或面积
延长AE，A1B1交于点F，连接D1F交B1C1于点G，如图，在正方体ABCD－A1B1C1D1中，平面ADD1A1∥平面BCC1B1，∵平面AFD1∩平面ADD1A1＝AD1，平面AFD1∩平面BCC1B1＝EG，
∴四边形AEGD1是梯形，且为平面AED1截正方体ABCD－A1B1C1D1的截面.
几何体的截面的相关计算，关键在于根据公理作出所求的截面，再运用解三角形的相关知识得以解决.
跟踪训练3　(2023·新乡模拟)如图，在棱长为2的正方体ABCD－A1B1C1D1中，E是棱CC1的中点，过A，D1，E三点的截面把正方体ABCD－A1B1C1D1分成两部分，则该截面的周长为
如图，取BC的中点F，连接EF，AF，BC1，E，F分别为棱CC1，BC的中点，则EF∥BC1，又在正方体中BC1∥AD1，则有EF∥AD1，所以平面AFED1为所求截面，因为正方体ABCD－A1B1C1D1的棱长为2，
一、单项选择题1.过正方体ABCD－A1B1C1D1的棱AB，BC的中点E，F作一个截面，使截面与底面ABCD所成二面角为45°，则此截面的形状为A.三角形或五边形 B.三角形或四边形C.正六边形 D.三角形或六边形
过棱AB，BC的中点E，F作正方体ABCD－A1B1C1D1的截面，∵二面角D1－EF－D，二面角B1－EF－B都大于45°，∴当截面为EFHJIG时，如图所示，为六边形；当截面为EFM时，如图所示，为三角形.
2.在长方体ABCD－A1B1C1D1中，若AB＝2，AD＝AA1＝4，E，F分别为BB1，A1D1的中点，过点A，E，F作长方体ABCD－A1B1C1D1的一个截面，则该截面的周长为
如图，连接AF，过点E作EP∥AF交B1C1于点P，连接FP，AE，即可得到截面AFPE，因为E为BB1的中点，EP∥AF，
因为AB＝2，AD＝AA1＝4，
3.(2023·承德模拟)在三棱锥P－ABC中，AB＋2PC＝9，E为线段AP上更靠近P的三等分点，过E作平行于AB，PC的平面，则该平面截三棱锥P－ABC所得截面的周长为A.5　　　B.6　　　C.8　　　D.9
如图所示，在三棱锥P－ABC中，过E分别作EF∥AB，EH∥PC，再分别过点H，F作HG∥AB，FG∥PC，可得E，F，G，H四点共面，因为AB⊄平面EFGH，EF⊂平面EFGH，所以AB∥平面EFGH，同理可证，PC∥平面EFGH，所以截面即为平行四边形EFGH，
又由E为线段AP上更靠近P的三等分点，且AB＋2PC＝9，
4.已知正方体ABCD－A1B1C1D1的棱长为2，M，N分别为A1B1，B1C1的中点，过M，N的平面所得截面为四边形，则该截面的最大面积为
5.从一个底面圆半径与高均为2的圆柱中挖去一个正四棱锥(以圆柱的上底面为正四棱锥底面的外接圆，下底面圆心为顶点)而得到的几何体如图所示，用一个平行于底面且距底面为1的平面去截这个几何体，则截面图形的面积为A.4π－4 B.4πC.4π－2 D.2π－2
截面图形应为圆面中挖去一个正方形，且圆的半径是2，则截面圆的面积为4π，
由圆锥中截面的性质，可得圆面中挖去一个正方形与正四棱锥的底面正方形相似，
所以截面图形的面积为4π－2.
6.在正方体ABCD－A1B1C1D1中，M，N分别为AD，C1D1的中点，过M，N，B1三点的平面截正方体ABCD－A1B1C1D1所得的截面形状为A.六边形 B.五边形C.四边形 D.三角形
如图，在AB上取点Q，且BQ＝3AQ，取CD的中点P，连接QM，BP，NP，B1Q.在DD1上取点R，且D1R＝3DR，连接NR，MR.
所以△QAM∽△PCB，所以∠AQM＝∠BPC.又AB∥CD，所以∠ABP＝∠BPC，所以∠ABP＝∠AQM，所以QM∥BP.
因为N，P分别为C1D1，CD的中点，所以PN∥CC1，且PN＝CC1.根据正方体的性质，可知BB1∥CC1，且BB1＝CC1，所以PN∥BB1，且PN＝BB1，所以四边形BPNB1是平行四边形，所以B1N∥BP，所以B1N∥QM.同理可得NR∥B1Q.所以五边形QMRNB1即为所求正方体的截面.
二、多项选择题7.用一个平面截正方体，则截面的形状不可能是A.锐角三角形 B.直角梯形C.正五边形 D.正六边形
对于A，截面图形如果是三角形，只能是锐角三角形，不可能是直角三角形和钝角三角形.如图所示的截面为△ABC.设DA＝a，DB＝b，DC＝c，所以AC2＝a2＋c2，AB2＝a2＋b2，BC2＝b2＋c2.
所以∠CAB为锐角.同理可求，∠ACB为锐角，∠CBA为锐角.所以△ABC为锐角三角形，故A不符合题意；
对于B，如图，截面图形如果是四边形，可能是正方形、矩形、菱形、一般梯形、等腰梯形，不可能是直角梯形，故B符合题意；
对于C，如图，当截面为五边形时，不可能出现正五边形，故C符合题意；对于D，当截面过棱的中点时，如图，即截面为正六边形，故D不符合题意.
8.已知正方体ABCD－A1B1C1D1的棱长为2，E，F，H是棱BC，D1C1，AA1上的动点(包含端点)，且满足CE＝D1F＝AH，则下列结论正确的是A.DB1⊥平面EFHB.存在E，F，H，使得点D到平面EFH的距离为1C.平面EFH截此正方体所得截面面积的最大值为D.平面EFH截此正方体所得截面的周长为定值
如图所示，建立空间直角坐标系，设CE＝D1F＝AH＝m，m∈[0,2]，则D(0,0,0)，E(m,2,0)，F(0，m,2)，H(2,0，m)，B1(2,2,2)，
同理可得DB1⊥EH，EF∩EH＝E，EF，EH⊂平面EFH，故DB1⊥平面EFH，故A正确；
设平面EFH分别与A1D1，AB，CC1交于P，Q，R，设P(p,0,2)，
如图，过点P作PM⊥HR于M，EN⊥HR于N，
三、填空题9.(2024·曲靖模拟)“中国天眼”(如图1)是世界最大单口径、最灵敏的射电望远镜，其形状可近似地看成一个球冠(球冠是球面被平面所截的一部分，如图2所示，截得的圆叫做球冠的底，垂直于截面的直径被截得的线段叫做球冠的高.若球面的半径是R，球冠的高度是h，则球冠的面积S＝2πRh).已知天眼的球冠的底的半径约为250米，天眼的反射面总面积(球冠面积)约为25万平方米，则天眼的球冠高度约为________米.
由题意得(R－h)2＋2502＝R2，则2Rh＝h2＋2502，则S＝2πRh＝πh2＋2502π＝250 000，
10.如图，在直三棱柱ABC－A1B1C1中，AB＝1，BC＝2，AC＝ ，AA1＝3，M为线段BB1上的一动点，则过A，M，C1三点的平面截该三棱柱所得截面的最小周长为___________.