第七章　§7.10　立体几何中的动态、轨迹问题-2025年新高考数学一轮复习（课件+讲义+练习）

这是一份第七章　§7.10　立体几何中的动态、轨迹问题-2025年新高考数学一轮复习（课件+讲义+练习），文件包含第七章§710立体几何中的动态轨迹问题pptx、第七章§710立体几何中的动态轨迹问题教师版docx、第七章§710立体几何中的动态轨迹问题同步练习docx、第七章§710立体几何中的动态轨迹问题-2025新高考一轮复习讲义学生版docx等4份课件配套教学资源，其中PPT共57页， 欢迎下载使用。

1、揣摩例题。课本上和老师讲解的例题，一般都具有一定的典型性和代表性。要认真研究，深刻理解，要透过“样板”，学会通过逻辑思维，灵活运用所学知识去分析问题和解决问题，特别是要学习分析问题的思路、解决问题的方法，并能总结出解题的规律。 2、精练习题。复习时不要搞“题海战术”，应在老师的指导下，选一些源于课本的变式题，或体现基本概念、基本方法的基本题，通过解题来提高思维能力和解题技巧，加深对所学知识的深入理解。在解题时，要独立思考，一题多思，一题多解，反复玩味，悟出道理。 3、加强审题的规范性。每每大考过后，总有同学抱怨没考好，纠其原因是考试时没有注意审题。审题决定了成功与否，不解决这个问题势必影响到高考的成败。那么怎么审题呢? 应找出题目中的已知条件 ;善于挖掘题目中的隐含条件 ;认真分析条件与目标的联系，确定解题思路 。 4、重视错题。“错误是最好的老师”，但更重要的是寻找错因，及时进行总结，三五个字，一两句话都行，言简意赅，切中要害，以利于吸取教训，力求相同的错误不犯第二次。
§7.10　立体几何中的动态、轨迹问题
“动态”问题是高考立体几何问题最具创新意识的题型，它渗透了一些“动态”的点、线、面等元素，给静态的立体几何题赋予了活力，题型更新颖.同时，由于“动态”的存在，也使立体几何题更趋多元化，将立体几何问题与平面几何中的解三角形问题、多边形面积问题以及解析几何问题之间建立桥梁，使得它们之间灵活转化.
题型一　平行、垂直中的动态轨迹问题
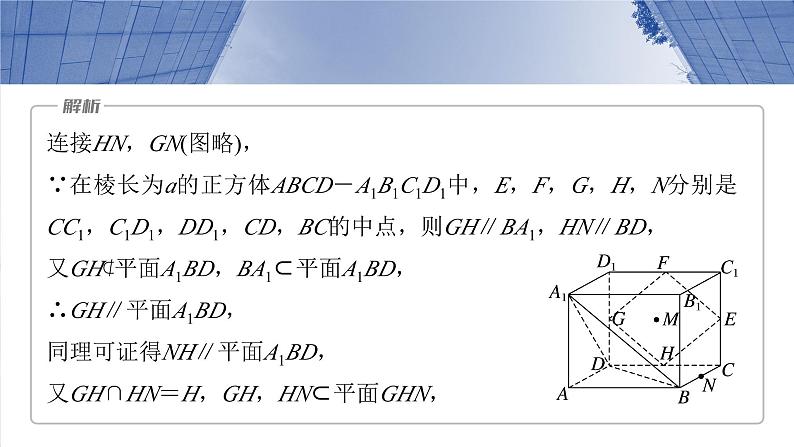
例1　如图，在棱长为a的正方体ABCD－A1B1C1D1中，E，F，G，H，N分别是CC1，C1D1，DD1，CD，BC的中点，M在四边形EFGH边上及其内部运动，若MN∥平面A1BD，则点M轨迹的长度是
连接HN，GN(图略)，∵在棱长为a的正方体ABCD－A1B1C1D1中，E，F，G，H，N分别是CC1，C1D1，DD1，CD，BC的中点，则GH∥BA1，HN∥BD，又GH⊄平面A1BD，BA1⊂平面A1BD，∴GH∥平面A1BD，同理可证得NH∥平面A1BD，又GH∩HN＝H，GH，HN⊂平面GHN，
∴平面A1BD∥平面GHN，又∵点M在四边形EFGH上及其内部运动，MN∥平面A1BD，则点M在线段GH上运动，即满足条件，
动点轨迹的判断一般根据线面平行、线面垂直的判定定理和性质定理，结合圆或圆锥曲线的定义推断出动点的轨迹，有时也可以利用空间向量的坐标运算求出动点的轨迹方程.
跟踪训练1　正四棱锥S－ABCD的底面边长为2，高为2，E是边BC的中点，动点P在正四棱锥表面上运动，并且总保持PE⊥AC，则动点P的轨迹的周长为
如图，设AC，BD交于O，连接SO，由正四棱锥的性质可得SO⊥平面ABCD，因为AC⊂平面ABCD，故SO⊥AC.又BD⊥AC，SO∩BD＝O，SO，BD⊂平面SBD，故AC⊥平面SBD.
由题意，PE⊥AC则动点P的轨迹为过E且垂直AC的平面与正四棱锥S－ABCD的交线，即平面EFG，则AC⊥平面EFG.
由线面垂直的性质可得平面SBD∥平面EFG，又由面面平行的性质可得EG∥SB，GF∥SD，EF∥BD，又E是边BC的中点，故EG，GF，EF分别为△SBC，△SDC，△BCD的中位线.
例2　已知长方体ABCD－A1B1C1D1的外接球的表面积为5π，AA1＝2，点P在四边形A1ACC1内，且直线BP与平面A1ACC1所成的角为 ，则长方体的体积最大时，动点P的轨迹长为
题型二　距离、角度有关的动态轨迹问题
因为长方体ABCD－A1B1C1D1的外接球的表面积为5π，设外接球的半径为R，
如图，设AC，BD相交于点O，因为BO⊥AC，BO⊥AA1，AC∩AA1＝A，AC，AA1⊂平面A1ACC1，
距离、角度有关的轨迹问题(1)距离：可转化为在一个平面内的距离关系，借助于圆锥曲线定义或者球和圆的定义等知识求解轨迹.(2)角度：直线与面成定角，可能是圆锥侧面；直线与定直线成等角，可能是圆锥侧面.
设底面等腰直角三角形ABC的直角边的边长为x(x>0)，
又∵顶点P到底面ABC的距离为4，
∴顶点P的轨迹是一个截面圆的圆周(球心在底面ABC和截面圆之间)且球心O到该截面圆的距离d2＝1，
例3　在矩形ABCD中，E是AB的中点，AD＝1，AB＝2，将△ADE沿DE折起得到△A′DE，设A′C的中点为M，若将△ADE沿DE翻折90°，则在此过程中动点M形成的轨迹长度为______.
题型三　翻折有关的动态轨迹问题
如图，设AC的中点为M0，△ADE沿DE翻折90°，此时平面A′DE⊥平面ABCD，取CD中点P，CE中点Q，PQ中点N，连接PQ，MP，MQ，MN，M0P，M0Q，M0N.
又MP∥A′D，MP⊄平面A′DE，A′D⊂平面A′DE，∴MP∥平面A′DE，同理MQ∥平面A′DE，
又∵MP∩MQ＝M，∴平面MPQ∥平面A′DE，又平面A′DE⊥平面ABCD，
故平面MPQ⊥平面ABCD，又平面MPQ∩平面ABCD＝PQ，MN⊥PQ，故MN⊥平面ABCD，又M0N⊂平面ABCD，∴MN⊥M0N，
翻折有关的轨迹问题(1)翻折过程中寻找不变的垂直的关系求轨迹.(2)翻折过程中寻找不变的长度关系求轨迹.(3)可以利用空间坐标运算求轨迹.
跟踪训练3　(2024·连云港模拟)在矩形ABCD中，AB＝ ，AD＝1，点E在CD上，现将△AED沿AE折起，使平面AED⊥平面ABC，当E从D运动到C时，求点D在平面ABC上的射影K的轨迹长度为
由题意，将△AED沿AE折起，使平面AED⊥平面ABC，在平面AED内过点D作DK⊥AE，垂足K为D在平面ABC上的射影，连接D′K，由翻折的特征知，
则∠D′KA＝90°，故K点的轨迹是以AD′为直径的圆上一段弧，
如图当E与C重合时，∠D′AC＝60°，
取O为AD′的中点，得到△OAK是正三角形.
一、单项选择题1.在正方体ABCD－A1B1C1D1中，Q是正方形B1BCC1内的动点，A1Q⊥BC1，则Q点的轨迹是A.点B1 B.线段B1CC.线段B1C1 D.平面B1BCC1
如图，连接A1C，因为BC1⊥A1Q，BC1⊥A1B1，A1Q∩A1B1＝A1，A1Q，A1B1⊂平面A1B1Q，所以BC1⊥平面A1B1Q，又B1Q⊂平面A1B1Q，所以BC1⊥B1Q，又BC1⊥B1C，所以点Q在线段B1C上.
2.(2023·佛山模拟)如图，正方体ABCD－A1B1C1D1的棱长为1，点P为正方形A1B1C1D1内的动点，满足直线BP与下底面ABCD所成角为60°的点P的轨迹长度为
直线BP与下底面ABCD所成的角等于直线BP与上底面A1B1C1D1所成的角，连接B1P，如图，因为BB1⊥平面A1B1C1D1，PB1⊂平面A1B1C1D1，所以BB1⊥PB1，故∠BPB1为直线BP与上底面A1B1C1D1所成的角，则∠BPB1＝60°，
3.如图，在三棱柱ABC－A1B1C1中，M为A1C1的中点，N为侧面BCC1B1上的一点，且MN∥平面ABC1，若点N的轨迹长度为2，则A.AC1＝4B.BC1＝4C.AB1＝6D.B1C＝6
如图，取B1C1的中点D，BB1的中点E，连接MD，DE，ME，由MD∥A1B1∥AB，DE∥BC1，又MD⊄平面ABC1，AB⊂平面ABC1，所以MD∥平面ABC1，同理可得DE∥平面ABC1，又MD∩DE＝D，MD，DE⊂平面MDE，所以平面MDE∥平面ABC1，又MN∥平面ABC1，故点N的轨迹为线段DE，
4.已知四棱柱ABCD－A1B1C1D1的底面ABCD为正方形，侧棱与底面垂直，点P是侧棱DD1上的点，且DP＝2PD1，AA1＝3，AB＝1.若点Q在侧面BCC1B1(包括其边界)上运动，且总保持AQ⊥BP，则动点Q的轨迹长度为
如图，在侧棱AA1上取一点R，使得AR＝2RA1，连接PR，BR，过点A作AN⊥BR交BR于点M，交BB1于点N，连接AC，CN，BD，由PR∥AD，可知PR⊥AN，BR，PR⊂平面BPR，BR∩PR＝R，从而AN⊥平面BPR，BP⊂平面BPR，所以BP⊥AN，又由BP在平面ABCD内的射影BD⊥AC，所以BP⊥AC，AN，AC⊂平面ACN，AN∩AC＝A，
知BP⊥平面ACN，CN⊂平面ACN，所以BP⊥CN，所以动点Q的轨迹为线段CN，在Rt△ABN，Rt△RAB中，∠BAN＝∠ARB，所以Rt△ABN∽Rt△RAB，
5.如图，已知正方体ABCD－A1B1C1D1的棱长为1，E，F分别是棱AD，B1C1的中点.若点P为侧面正方形ADD1A1内(含边界)动点，且B1P∥平面BEF，则点P的轨迹长度为
取A1D1的中点M，连接AM，B1M，AB1，EM，FM，如图所示，在正方体ABCD－A1B1C1D1中，AD∥B1C1且AD＝B1C1，因为E，F分别是棱AD，B1C1的中点，则AE∥B1F且AE＝B1F，所以四边形AB1FE为平行四边形，则AB1∥EF，因为AB1⊄平面BEF，EF⊂平面BEF，所以AB1∥平面BEF，同理可证AM∥平面BEF，
因为AB1∩AM＝A，AB1，AM⊂平面AB1M，所以平面AB1M∥平面BEF，因为AM⊂平面AA1D1D，若P∈AM，则B1P⊂平面AB1M，所以B1P∥平面BEF，所以点P在侧面AA1D1D内的轨迹为线段AM，
6.已知菱形ABCD边长为2，∠ABC＝60°，沿对角线AC折叠成三棱锥B′－ACD，使得二面角B′－AC－D为60°，设E为B′C的中点，F为三棱锥B′－ACD表面上动点，且总满足AC⊥EF，则点F轨迹的长度为
连接AC，BD交于点O，连接OB′，四边形ABCD为菱形，∠ABC＝60°，所以AC⊥BD，OB′⊥AC，△ABC，△ACD，△AB′C均为正三角形，所以∠B′OD为二面角B′－AC－D的平面角，于是∠B′OD＝60°，又因为OB′＝OD，所以△B′OD为正三角形，
取OC的中点P，取CD的中点Q，连接EP，EQ，PQ，所以PQ∥OD，EP∥OB′，
所以AC⊥EP，AC⊥PQ，EP∩PQ＝P，所以AC⊥平面EPQ，所以在三棱锥B′－ACD表面上，满足AC⊥EF的点F轨迹为△EPQ，
二、多项选择题7.(2024·济南模拟)已知正方体ABCD－A1B1C1D1的各顶点均在表面积为12π的球面上，P为该球面上一动点，则A.存在无数个点P，使得PA∥平面A1B1C1D1B.当平面PAA1⊥平面CB1D1时，点P的轨迹长度为2πC.当PA∥平面A1B1CD时，点P的轨迹长度为2πD.存在无数个点P，使得平面PAD⊥平面PBC
因为该球的表面积为4πr2＝12π，
且正方体的棱长满足(2r)2＝3a2＝12，故棱长a＝2，
选项A，由题意可知平面ABCD∥平面A1B1C1D1，且PA∥平面A1B1C1D1，
故PA⊂平面ABCD，则P的轨迹为正方形ABCD的外接圆，故有无数个点P满足，故A正确；
选项B，易知AC1⊥平面CB1D1，且平面PAA1⊥平面CB1D1，PA⊂平面PAA1，故P的轨迹为矩形AA1C1C的外接圆，
选项C，因为PA∥平面A1B1CD，设过PA且与平面A1B1CD平行的平面为α，
选项D，若平面PAD⊥平面PBC，则点P在以四边形ABCD为轴截面的某个圆柱面上，该圆柱面与球面交线为曲线，故有无数个点P满足，故D正确.
8.(2023·长沙模拟)在棱长为1的正方体ABCD－A1B1C1D1中，M为正方体表面上的动点，N为线段AC1上的动点，若直线AM与AB的夹角为 ，则下列说法正确的是A.点M的轨迹确定的图形是平面图形
如图，建立空间直角坐标系，则D(0,1,0)，C1(1,1,1)，
当点M在底面A1B1C1D1和侧面CC1D1D(不包含边界)上时，点M到直线AB的距离大于AB的长度，
当点M在侧面AA1B1B和底面ABCD上时，可知线段AB1，AC满足题意；
当点M在侧面BCC1B1上时，由AB⊥BM，可知BM＝AB，此时弧B1C为所求.∴M点的轨迹为线段AC，AB1，弧B1C，显然线段AC，AB1，弧B1C不共面，∴A错误；
对于C，若M在线段AC上，则C1M的最小值为1，同理，若M在线段AB1上，则C1M的最小值也为1，
对于D，M(1，y，z)(0≤y≤1,0≤z≤1)，且y2＋z2＝1，由题意设N(λ，λ，λ)，λ∈[0,1]，
当且仅当y＝z＝λ，且y2＋z2＝1，
三、填空题9.已知正方体ABCD－A1B1C1D1的棱长为2，M为棱B1C1的中点，N为底面正方形ABCD上一动点，且直线MN与底面ABCD所成的角为 ，则动点N的轨迹长度为________.
如图所示，取BC中点G，连接MG，NG，由正方体的特征可知，MG⊥底面ABCD，故MN与底面ABCD的夹角即为∠MNG，
又N在底面正方形ABCD上，即点N的轨迹为图示中的圆弧 ，
10.如图所示，在平行四边形ABCD中，E为AB中点，DE⊥AB，DC＝8，DE＝6.沿着DE将△ADE折起，使A到达点A′的位置，且平面A′DE⊥平面ADE.设P为△A′DE内的动点，若∠EPB＝∠DPC，则点P的轨迹长度为______.
建立如图所示的空间直角坐标系，则D(0,0,0)，C(0,8,0)，E(6,0,0)，B(6,4,0)，设P(x,0，z)，
∵∠EPB＝∠DPC，∴cs∠EPB＝cs∠DPC，
整理化简得x2＋z2－16x＋48＝0，