资料中包含下列文件,点击文件名可预览资料内容
















还剩33页未读,
继续阅读
成套系列资料,整套一键下载
第八章 必刷小题16 圆锥曲线-2025年新高考数学一轮复习(课件+讲义+练习)
展开
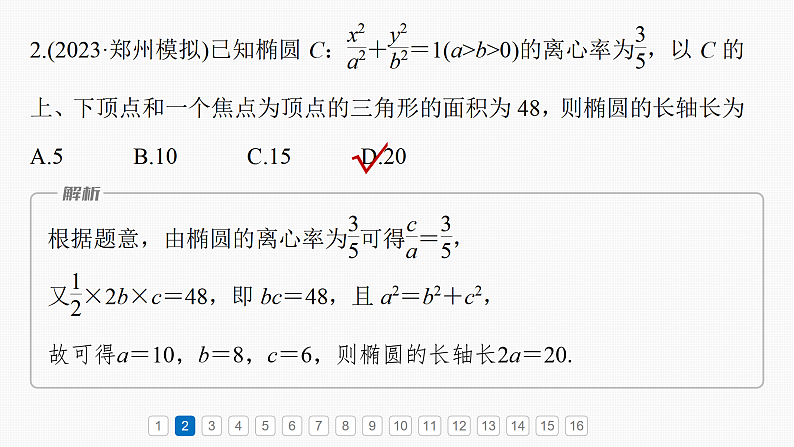
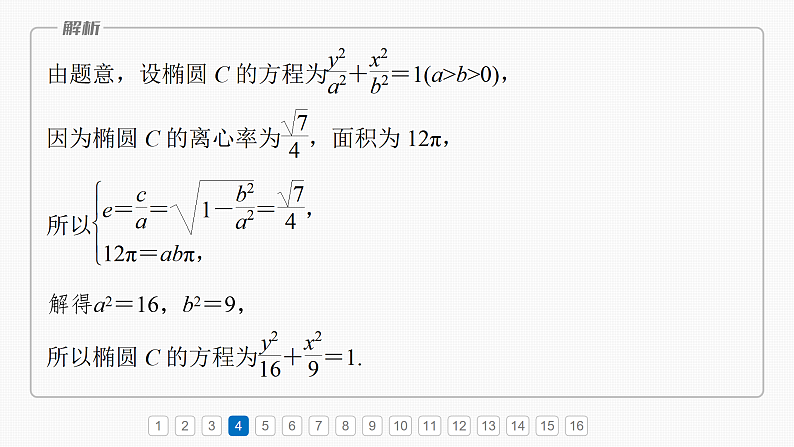
高考数学一轮复习策略 1、揣摩例题。课本上和老师讲解的例题,一般都具有一定的典型性和代表性。要认真研究,深刻理解,要透过“样板”,学会通过逻辑思维,灵活运用所学知识去分析问题和解决问题,特别是要学习分析问题的思路、解决问题的方法,并能总结出解题的规律。 2、精练习题。复习时不要搞“题海战术”,应在老师的指导下,选一些源于课本的变式题,或体现基本概念、基本方法的基本题,通过解题来提高思维能力和解题技巧,加深对所学知识的深入理解。在解题时,要独立思考,一题多思,一题多解,反复玩味,悟出道理。 3、加强审题的规范性。每每大考过后,总有同学抱怨没考好,纠其原因是考试时没有注意审题。审题决定了成功与否,不解决这个问题势必影响到高考的成败。那么怎么审题呢? 应找出题目中的已知条件 ;善于挖掘题目中的隐含条件 ;认真分析条件与目标的联系,确定解题思路 。 4、重视错题。“错误是最好的老师”,但更重要的是寻找错因,及时进行总结,三五个字,一两句话都行,言简意赅,切中要害,以利于吸取教训,力求相同的错误不犯第二次。第八章必刷小题16 圆锥曲线一、单项选择题12345678910111213141516√√故可得a=10,b=8,c=6,则椭圆的长轴长2a=20.123456789101112131415163.(2024·长春模拟)已知M为抛物线C:x2=2py(p>0)上一点,点M到C的焦点的距离为7,到x轴的距离为5,则p等于A.3 B.4 C.5 D.6√123456789101112131415164.(2023·河北衡水中学检测)阿基米德(公元前287年—公元前212年)不仅是著名的物理学家,也是著名的数学家,他利用“逼近法”得到椭圆的面积除以圆周率等于椭圆的长半轴长与短半轴长的乘积.若椭圆C的对称轴为坐标轴,焦点在y轴上,且椭圆C的离心率为 ,面积为12π,则椭圆C的方程为√12345678910111213141516解得a2=16,b2=9,1234567891011121314151612345678910111213141516√设线段PF2的中点为M,连接PF1,MF1,如图所示,则F1F2为圆O的一条直径,则F1M⊥PF2,因为M为PF2的中点,则|PF1|=|F1F2|=2c=2,则|PF2|=2a-|PF1|=2,所以△PF1F2为等边三角形,12345678910111213141516123456789101112131415166.(2023·石家庄模拟)已知,点P是抛物线C:y2=4x上的动点,过点P向y轴作垂线,垂足记为点N,点M(3,4),则|PM|+|PN|的最小值是√12345678910111213141516由抛物线C:y2=4x知,焦点F(1,0),准线方程为x=-1,过点P作抛物线准线的垂线,垂足为Q,如图,由抛物线定义知|PN|+|PM|=|PQ|-1+|PM|=|PF|+|PM|-1,当F,P,M三点共线时,|PM|+|PN|取得最小值,12345678910111213141516√作PM⊥x轴于点M,如图,则∠PF2M=60°,由题意知F2(c,0),由双曲线的定义知|PF1|=2a+2c,而|F1F2|=2c,在△PF1F2中,由余弦定理得|PF1|2=|PF2|2+|F1F2|2-2|PF2|·|F1F2|·cos∠PF2F1,1234567891011121314151612345678910111213141516123456789101112131415168.(2023·连云港模拟)直线l:y=-x+1与抛物线C:y2=4x交于A,B两点,圆M过两点A,B且与抛物线C的准线相切,则圆M的半径是A.4 B.10C.4或10 D.4或12√可设A(x1,y1),B(x2,y2),则y1+y2=-4,即y1+y2=-x1+1-x2+1=-4,则x1+x2=6,可得AB的中点坐标为P(3,-2),易知,直线l过抛物线焦点(1,0),则|AB|=x1+1+x2+1=8,12345678910111213141516且AB的垂直平分线方程为y-(-2)=1×(x-3),即y=x-5,则可设圆M的圆心为M(a,b),半径为r,所以b=a-5,则圆M的方程为(x-a)2+(y-b)2=r2,即(x-a)2+(y-a+5)2=r2,1234567891011121314151612345678910111213141516则16+2(a-3)2=r2, ①又因为圆M与抛物线C的准线相切,所以|a+1|=r,即(a+1)2=r2, ②二、多项选择题12345678910111213141516A.双曲线C的实轴长为2B.双曲线C的焦点到渐近线的距离为mC.若(2,0)是双曲线C的一个焦点,则m=2D.若双曲线C的两条渐近线相互垂直,则m=2√√12345678910111213141516因为(2,0)是双曲线C的一个焦点,1234567891011121314151612345678910111213141516√√√对于选项B,当点P为椭圆C的右顶点时,可得|PF1|max=a+c=6,故B正确;对于选项C,△F1PF2的周长为2a+2c=12,故C错误;对于选项D,当点P为椭圆C的短轴的端点时,可得|PF1|=|PF2|=a=4,|F1F2|=2c=4,此时△F1PF2为等边三角形,故D正确.12345678910111213141516√√√12345678910111213141516根据抛物线的性质知,MN过焦点F时,12345678910111213141516过点M,N,P分别作准线的垂线MM′,NN′,PP′,垂足分别为M′,N′,P′(图略),所以|MM′|=|MF|,|NN′|=|NF|.12345678910111213141516√√√12345678910111213141516由题意得a=2,12345678910111213141516所以|QF1|的取值范围是[a-c,a+c],设椭圆的上顶点为A(0,b),F1(-c,0),F2(c,0),1234567891011121314151612345678910111213141516当且仅当|QF1|=|QF2|=2时,等号成立,又|QF1|+|QF2|=4,三、填空题13.(2023·烟台模拟)写出一个满足以下三个条件的椭圆的方程_______________________.①中心为坐标原点;②焦点在坐标轴上;12345678910111213141516(答案不唯一)12345678910111213141516123456789101112131415161234567891011121314151612345678910111213141516y2=4x12345678910111213141516设|NF|=4t(t>0),①②且12=2pa,即pa=6, ③①②联立得12a2-20ap+3p2=0,得2a=3p或6a=p,由于0
相关资料
更多








