新高考数学三轮冲刺 北京卷押题练习 第10题 空间几何体的结构（2份打包，原卷版+解析版）

这是一份新高考数学三轮冲刺 北京卷押题练习 第10题 空间几何体的结构（2份打包，原卷版+解析版），文件包含新高考数学三轮冲刺北京卷押题练习第10题空间几何体的结构原卷版doc、新高考数学三轮冲刺北京卷押题练习第10题空间几何体的结构解析版doc等2份试卷配套教学资源，其中试卷共23页， 欢迎下载使用。

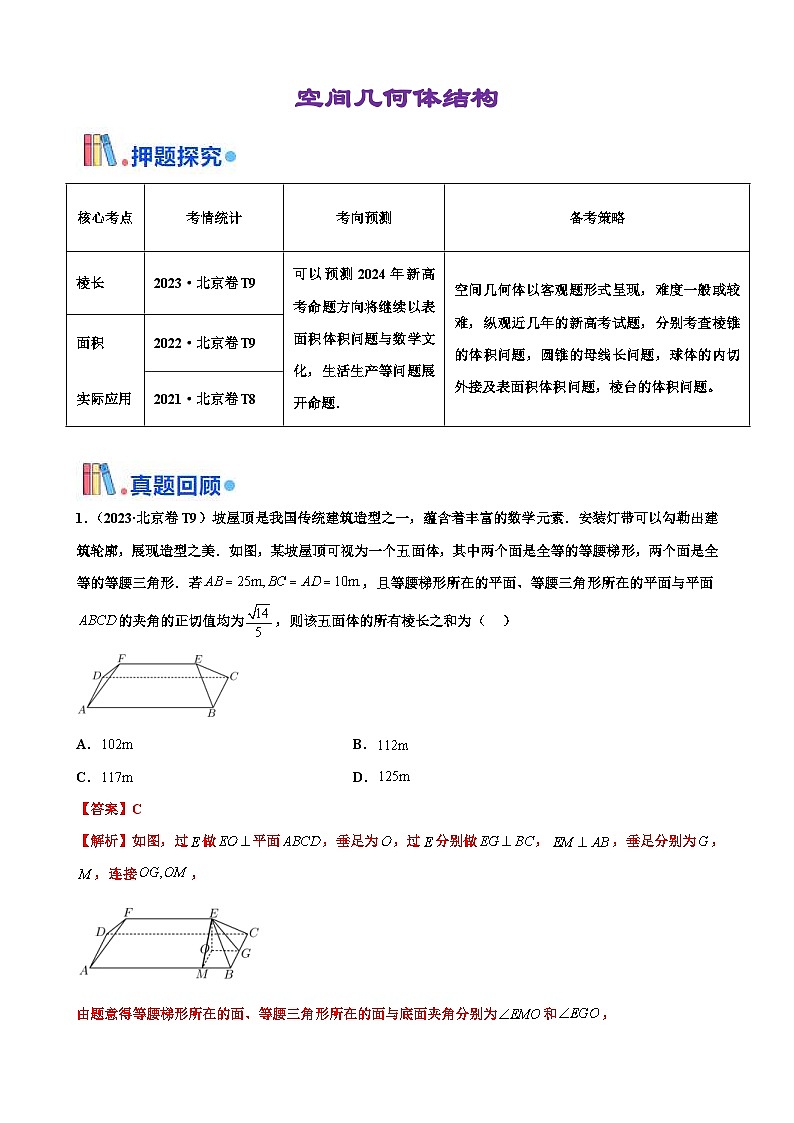
1．（2023·北京卷T9）坡屋顶是我国传统建筑造型之一，蕴含着丰富的数学元素．安装灯带可以勾勒出建筑轮廓，展现造型之美．如图，某坡屋顶可视为一个五面体，其中两个面是全等的等腰梯形，两个面是全等的等腰三角形．若 SKIPIF 1 < 0 ，且等腰梯形所在的平面、等腰三角形所在的平面与平面 SKIPIF 1 < 0 的夹角的正切值均为 SKIPIF 1 < 0 ，则该五面体的所有棱长之和为（ ）

A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
2．（2022·北京卷T9）已知正三棱锥 SKIPIF 1 < 0 的六条棱长均为6，S是 SKIPIF 1 < 0 及其内部的点构成的集合．设集合 SKIPIF 1 < 0 ，则T表示的区域的面积为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
3．（2021·北京卷T8）某一时间段内，从天空降落到地面上的雨水，未经蒸发、渗漏、流失而在水平面上积聚的深度，称为这个时段的降雨量（单位： SKIPIF 1 < 0 ）．24h降雨量的等级划分如下：

在综合实践活动中，某小组自制了一个底面直径为200 mm，高为300 mm的圆锥形雨量器.若一次降雨过程中，该雨量器收集的24h的雨水高度是150 mm（如图所示)，则这24h降雨量的等级是
A．小雨B．中雨C．大雨D．暴雨
立体几何基础公式
所有椎体体积公式： SKIPIF 1 < 0
所有柱体体积公式： SKIPIF 1 < 0
球体体积公式： SKIPIF 1 < 0
球体表面积公式： SKIPIF 1 < 0
圆柱： SKIPIF 1 < 0
圆锥： SKIPIF 1 < 0
长方体（正方体、正四棱柱）的体对角线的公式
已知长宽高求体对角线： SKIPIF 1 < 0
已知共点三面对角线求体对角线： SKIPIF 1 < 0
棱长为 SKIPIF 1 < 0 的正四面体的内切球的半径为 SKIPIF 1 < 0 ,外接球的半径为 SKIPIF 1 < 0 .
4.求解几何体表面积的类型及方法
（1）求多面体的表面积：只需将它们沿着棱“剪开”展成平面图形，利用求平面图形面积的方法求多面体的表面积；
（2）求旋转体的表面积：可以从旋转体的形成过程及其几何特征入手，将其展开后求表面积，但要搞清它们的底面半径、母线长与对应侧面展开图中的边长关系；
（3）求不规则几何体的表面积：通常将所给几何体分割成基本的柱体、锥体、台体，先求出这些基本的柱体、锥体、台体的表面积，再通过求和或作差，求出所给几何体的表面积.
5.求空间几何体体积的常用方法
（1）公式法：对于规则几何体的体积问题，可以直接利用公式进行求解；
（2）割补法：把不规则的几何体分割成规则的几何体，然后进行体积计算；或者把不规则的几何体补成规则的几何体，不熟悉的几何体补成熟悉的几何体，便于计算其体积；
（3）等体积法：一个几何体无论怎样转化，其体积总是不变的.如果一个几何体的底面面积和高较难求解时，我们可以采用等体积法进行求解.等体积法也称等积转化或等积变形，它是通过选择合适的底面来求几何体体积的一种方法，多用来解决有关锥体的体积，特别是三棱锥的体积.

1．已知一个正六棱台的两底面边长分别为 SKIPIF 1 < 0 ，高是 SKIPIF 1 < 0 ，则该棱台的斜高为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
2．将一个棱长为1的正方体放入一个圆柱内，正方体可自由转动，则该圆柱体积的最小值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
3．如图①所示，圆锥绣球是虎耳草科绣球属植物，在中国主要分布于西北、华东、华南、西南等地区，抗虫害能力强，其花序硕大，类似于圆锥形，因此得名．现将某圆锥绣球近似看作如图②所示的圆锥模型，已知 SKIPIF 1 < 0 ，直线 SKIPIF 1 < 0 与圆锥底面所成角的余弦值为 SKIPIF 1 < 0 ，则该圆锥的侧面积为（ ）

A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
4． SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，则将 SKIPIF 1 < 0 以 SKIPIF 1 < 0 为轴旋转一周所形成的几何体的体积为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
5．《天工开物》是我国明代科学家宋应星所著的一部综合性科学技术著作，书中记载了一种制造瓦片的方法.某校高一年级计划实践这种方法，为同学们准备了制瓦用的粘土和圆柱形的木质圆桶，圆桶底面外圆的直径为 SKIPIF 1 < 0 ，高为 SKIPIF 1 < 0 .首先，在圆桶的外侧面均匀包上一层厚度为 SKIPIF 1 < 0 的粘土，然后，沿圆桶母线方向将粘土层分割成四等份（如图），等粘土干后，即可得到大小相同的四片瓦.每位同学制作四片瓦，全年级共500人，需要准备的粘土量（不计损耗）与下列哪个数字最接近.（参考数据： SKIPIF 1 < 0 ）（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
6．一个边长为10cm的正方形铁片，把图中所示的阴影部分裁下，然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器，则这个容器侧面与底面的夹角正切值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
7．已知一个圆锥的高与其底面圆的半径相等，且体积为 SKIPIF 1 < 0 ．在该圆锥内有一个正方体，其下底面的四个顶点在圆锥的底面内，上底面的四个顶点在圆锥的侧面上，则该正方体的棱长为（ ）
A． SKIPIF 1 < 0 B．1C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
8．已知平面 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 间的距离为3，定点 SKIPIF 1 < 0 ，设集合 SKIPIF 1 < 0 ，则S表示的曲线的长度为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
9．“木桶效应”是一个有名的心理效应，是指木桶盛水量的多少，取决于构成木桶的最短木板的长度，而不取决于构成木桶的长木板的长度，常被用来寓意一个短处对于一个团队或者一个人的影响程度.某同学认为，如果将该木桶斜放，发挥长板的作用，在短板存在的情况下，也能盛较多的水.根据该同学的说法，若有一个如图①所示的圆柱形木桶，其中一块木板有缺口，缺口最低处与桶口距离为2，若按照图②的方式盛水，形成了一个椭圆水面，水面刚好与左边缺口最低处M和右侧桶口N齐平，且MN为该椭圆水面的长轴.则此时比图①盛水方式多盛的水的体积为（ ）

A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
10．南水北调工程缓解了北方一些地区水资源短缺问题，其中一部分水蓄入某水库.已知该水库水位为海拔 SKIPIF 1 < 0 时，相应水面的面积为 SKIPIF 1 < 0 ；水位为海拔 SKIPIF 1 < 0 时，相应水面的面积为 SKIPIF 1 < 0 ，将该水库在这两个水位间的形状看作一个棱台，则该水库水位从海拔 SKIPIF 1 < 0 上升到 SKIPIF 1 < 0 时，增加的水量约为（ ）（ SKIPIF 1 < 0 ，棱台体积公式 SKIPIF 1 < 0 ，其中 SKIPIF 1 < 0 ， SKIPIF 1 < 0 分别为棱台的上下底的面积， SKIPIF 1 < 0 是棱台的高）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
11．金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥.某金字塔的侧面积之和等于底面积的2倍，则该金字塔侧面三角形与底面正方形所成角的正切值为（ ）
A．1B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
12．随着北京中轴线申遗工作的进行，古建筑备受关注．故宫不仅是世界上现存规模最大、保存最为完整的木质结构古建筑之一，更是北京中轴线的“中心”．图1是古建筑之首的太和殿，它的重檐庑（wŭ）殿顶可近似看作图2所示的几何体，其中底面 SKIPIF 1 < 0 题矩形， SKIPIF 1 < 0 ，四边形 SKIPIF 1 < 0 是两个全等的等腰梯形， SKIPIF 1 < 0 是两个全等的等腰三角形．若 SKIPIF 1 < 0 ，则该几何体的体积为（ ）

（图1） （图2）
A．90B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D．135
13．已知正四棱锥 SKIPIF 1 < 0 ，底面边长为2，体积为 SKIPIF 1 < 0 ，则这个四棱锥的侧棱长为 .
14．某圆柱体的底面半径为2，母线长为4，则该圆柱体的表面积为 ．
15．若一个圆锥的轴截面是等边三角形，其面积为 SKIPIF 1 < 0 ，则这个圆锥的侧面积是 ．
16．如图，六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的．已知螺帽的底面正六边形边长为2 cm，高为2 cm，内孔半径为0.5 cm，则此六角螺帽毛坯的体积是 cm3.
17．如图，一个底面半径为 SKIPIF 1 < 0 的圆柱形量杯中装有适量的水，若放入一个半径为 SKIPIF 1 < 0 的实心铁球，水面高度恰好升高 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 ．
18．圆柱形容器内部盛有高度为 SKIPIF 1 < 0 的水，若放入三个相同的球（球的半径与圆柱的底面半径相同）后，水恰好淹没最上面的球（如图所示），则球的半径是 SKIPIF 1 < 0 ．
19．已知正四棱锥的高为4，侧面积为 SKIPIF 1 < 0 ，则该棱锥的侧棱长为 .
20．作为我国古代称量粮食的量器，米斗有着吉祥的寓意，是丰饶富足的象征，带有浓郁的民间文化韵味．右图是一件清代老木米斗，可以近似看作正四棱台，测量得其内高为 SKIPIF 1 < 0 ，两个底面内棱长分别为 SKIPIF 1 < 0 和 SKIPIF 1 < 0 ，则估计该米斗的容积为 SKIPIF 1 < 0 ．
核心考点
考情统计
考向预测
备考策略
棱长
2023·北京卷T9
可以预测2024年新高考命题方向将继续以表面积体积问题与数学文化，生活生产等问题展开命题．
空间几何体以客观题形式呈现，难度一般或较难，纵观近几年的新高考试题，分别考查棱锥的体积问题，圆锥的母线长问题，球体的内切外接及表面积体积问题，棱台的体积问题。
面积
2022·北京卷T9
实际应用
2021·北京卷T8
等级
24h降雨量（精确到0.1）
……
……
小雨
0.1~9.9
中雨
10.0~24.9
大雨
25.0~49.9
暴雨
50.0~99.9
……
……