

数学八年级上册3.2 勾股定理的逆定理同步训练题
展开TOC \ "1-3" \h \u
\l "_Tc2652" 【题型1 判断三边能否构成直角三角形】 PAGEREF _Tc2652 \h 1
\l "_Tc7249" 【题型2 图形上与已知两点构成直角三角形的点】 PAGEREF _Tc7249 \h 2
\l "_Tc32186" 【题型3 在网格中判断直角三角形】 PAGEREF _Tc32186 \h 2
\l "_Tc9878" 【题型4 勾股数的探究】 PAGEREF _Tc9878 \h 3
\l "_Tc19434" 【题型5 利用勾股定理的逆定理证明】 PAGEREF _Tc19434 \h 5
\l "_Tc9893" 【题型6 利用勾股定理的逆定理求解】 PAGEREF _Tc9893 \h 5
\l "_Tc30460" 【题型7 勾股逆定理的应用】 PAGEREF _Tc30460 \h 6
\l "_Tc25171" 【题型8 勾股定理及其逆定理的综合】 PAGEREF _Tc25171 \h 7
【知识点 勾股定理的逆定理】
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.
【题型1 判断三边能否构成直角三角形】
【例1】(2023春·黑龙江哈尔滨·八年级哈尔滨德强学校校考期中)由线段a、b、c组成的三角形是直角三角形的是( )
A.a=5,b=3,c=3B.a=13,b=15,c=14
C.a=6,b=4,c=5D.a=7,b=24,c=25
【变式1-1】(2023春·湖北孝感·八年级统考期中)一个三角形的三边长分别为a,b,c,且满足a+ba-b=c2,则这个三角形是( )
A.等腰三角形B.直角三角形C.锐角三角形D.不确定
【变式1-2】(2023春·八年级单元测试)如图,以△ABC的两边BC、AC分别向外作正方形,它们的面积分别是S1,S2,若S1=2,S2=3,AB2=5,则△ABC的形状是________三角形.
【变式1-3】(2023春·广东惠州·八年级校考期中)有四种说法:①三个内角之比为5:6:1; ②三边形长分别为:2,7,5;③三边之长为9、40、41;④三边之比为1.5∶2∶3.其中是直角三角形的有___________(填序号).
【题型2 图形上与已知两点构成直角三角形的点】
【例2】(2023春·全国·八年级专题练习)同一平面内有A,B,C三点,A,B两点之间的距离为5cm,点C到直线AB的距离为2cm,且△ABC为直角三角形,则满足上述条件的点C有______个.
【变式2-1】(2023春·八年级单元测试)在如图所示的5×5的方格图中,点A和点B均为图中格点.点C也在格点上,满足△ABC为以AB为斜边的直角三角形.这样的点C有( )
A.1个B.2个C.3个D.4个
【变式2-2】(2023春·全国·八年级专题练习)点 A(2,m),B(2,m-5)在平面直角坐标系中,点O为坐标原点.若△ABO是直角三角形,则m的值不可能是( )
A.4B.2C.1D.0
【变式2-3】(2023春·全国·八年级专题练习)如图,方格纸中的每个小正方形的边长均为1,点A,B在小正方形的顶点上,在图中画ΔABC(点C在小正方形的顶点上),使ΔABC为直角三角形,并说明理由.(要求画出两个,且两个三角形不全等)
【题型3 在网格中判断直角三角形】
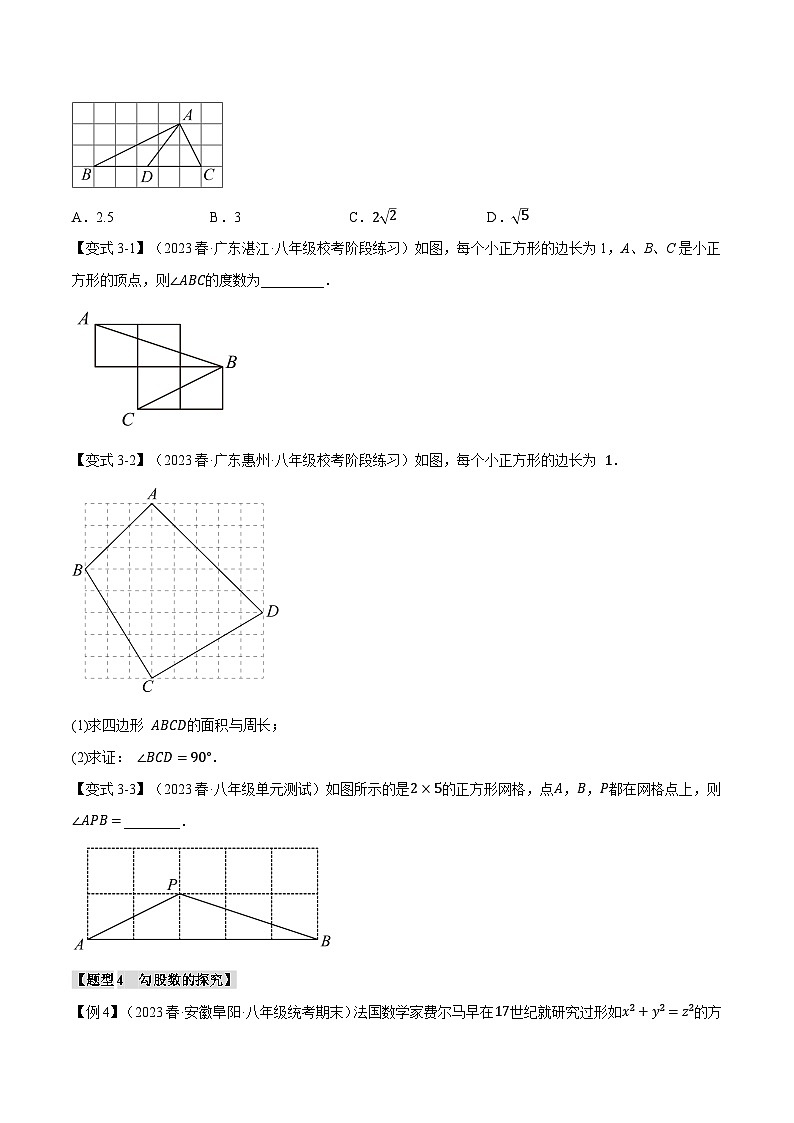
【例3】(2023春·北京西城·八年级校考期中)如图,在正方形网格中,每个小正方形的边长为1,△ABC的三个顶点A,B,C都在格点上,AD是BC边上的中线,那么AD的长为( )
A.2.5B.3C.22D.5
【变式3-1】(2023春·广东湛江·八年级校考阶段练习)如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为_________.
【变式3-2】(2023春·广东惠州·八年级校考阶段练习)如图,每个小正方形的边长为 1.
(1)求四边形 ABCD的面积与周长;
(2)求证: ∠BCD=90°.
【变式3-3】(2023春·八年级单元测试)如图所示的是2×5的正方形网格,点A,B,P都在网格点上,则∠APB=________.
【题型4 勾股数的探究】
【例4】(2023春·安徽阜阳·八年级统考期末)法国数学家费尔马早在17世纪就研究过形如x2+y2=z2的方程,显然,这个方程有无数组解.我们把满足该方程的正整数的解x,y,z叫做勾股数.如3,4,5就是一组勾股数.
(1)请你再写出两组勾股数:(___________),(___________);
(2)在研究直角三角形的勾股数时,古希腊的哲学家柏拉图曾指出:如果n表示大于1的整数,x=2n,y=n2-1,z=n2+1,那么,以x,y,z为三边的三角形为直角三角形(即x,y,z为勾股数),请你加以证明.
【变式4-1】(2023春·四川达州·八年级校考期中)以下列各组数据中的三个数,其中是勾股数的是( )
A. 3,4,5B.6,8,10C.1,2,3D.2,3,4
【变式4-2】(2023春·全国·八年级专题练习)一个直角三角形三边长都是正整数,这样的直角三角形叫做“整数直角三角形”,这三个整数叫做一组“勾股数”老师给出了下表(其中m,n为正整数,且m>n):
(1)探究a,b,c与m,n之间的关系并用含m,n的代数式表示:a=______,b=______,c=______.
(2)以a,b,c为边长的三角形是否一定为直角三角形?请说明理由.
【变式4-3】(2023春·重庆北碚·八年级西南大学附中校考期中)勾股定理是一个基本的几何定理,早在我国西汉时期算书《周髀算经》就有“勾三股四弦五”的记载.如果一个直角三角形三边长都是正整数,这样的直角三角形叫“整数直角三角形”;这三个整数叫做一组“勾股数”,如:3,4,5;5,12,13;7,24,25;8,15,17;9,40,41等等都是勾股数.
(1)小李在研究勾股数时发现,某些整数直角三角形的斜边能写成两个整数的平方和,有一条直角边能写成这两个整数的平方差.如3,4,5中,5=22+12,3=22﹣12;5,12,13中,13=32+22,5=32﹣22;请证明:m,n为正整数,且m>n,若有一个直角三角形斜边长为m2+n2,有一条直角长为m2﹣n2,则该直角三角形一定为“整数直角三角形”;
(2)有一个直角三角形两直角边长分别为7a-7和150-30b,斜边长415,且a和b均为正整数,用含b的代数式表示a,并求出a和b的值;
(3)若c1=a12+b12,c2=a22+b22,其中,a1、a2、b1、b2均为正整数.证明:存在一个整数直角三角形,其斜边长为c1•c2.
【题型5 利用勾股定理的逆定理证明】
【例5】(2023·江苏·八年级假期作业)如图,已知CD⊥AB,垂足为D,BD=1,CD=2,AD=4.求证:∠ACB=90°.
【变式5-1】(2023·江苏·八年级假期作业)在△ABC的三边分别是a、b、c,且a=n2-1,b=2n,c=n2+1,判断△ABC的形状,证明你的结论.
【变式5-2】(2023春·八年级课时练习)如图,以△ABC的每一条边为边作三个正方形.已知这三个正方形构成的图形中,绿色部分的面积与蓝色部分的面积相等,则△ABC是直角三角形吗?请证明你的判断.
【变式5-3】(2023春·江苏盐城·八年级统考期中)如图,在△ABC中,AB=7,AC=25,AD是中线,点E在AD的延长线上,且AD=ED=12.
(1)求证:△CDE≌△BDA;
(2)证明:CE⊥AE;
(3)求△ABC的面积.
【题型6 利用勾股定理的逆定理求解】
【例6】(2023春·山西吕梁·八年级统考期末)如图,在△ABC中,AB=5,BC=4,AC=3,将三角形纸片沿AD折叠,使点C落在AB边上的点E处,则△BDE的周长为( )
A.3B.4C.5D.6
【变式6-1】(2023春·湖北襄阳·八年级统考期中)如图,在△ABC中,点D在AB上,AB=AC,BC=5,BD=3,CD=4.求AC的长.
【变式6-2】(2023春·河南开封·八年级统考期末)已知△ABC的三边分别为a、b、c,且满足a+2b-112+2a-b-2=10c-25-c2,请你判断△ABC的形状,并求出其周长与面积.
【变式6-3】(2023春·陕西榆林·八年级校考期末)已知在△ACB中,AC=12,BC=5,AB=13,点E为边AC上的动点,点F为边AB上的动点,则FE+EB的最小值是_________.
【题型7 勾股逆定理的应用】
【例7】(2023春·广东广州·八年级统考期中)如图,在笔直的公路AB旁有一座山,从山另一边的C处到公路上的停靠站A的距离为AC=15km,与公路上另一停靠站B的距离为BC=20km,停靠站A、B之间的距离为AB=25km,为方便运输货物现要从公路AB上的D处开凿隧道修通一条公路到C处,且CD⊥AB.
(1)请判断△ABC的形状?
(2)求修建的公路CD的长.
【变式7-1】(2023春·广西南宁·八年级南宁市天桃实验学校校考阶段练习)森林火灾是一种常见的自然灾害,危害很大.随着中国科技、经济的不断发展,开始应用飞机洒水的方式扑灭火源.如图,△ABC区域内是一片森林,有一台救火飞机沿东西方向AB,由点A飞向点B,已知点C为其中一个着火点,且点C与点A,B的距离分别为600m和800m,又AB=1000m,飞机中心周围500m以内可以受到洒水影响.
(1)求△ABC的面积.
(2)着火点C能否受到洒水影响?为什么?
【变式7-2】(2023春·广西桂林·八年级统考期中)一根12米的电线杆AB,用铁丝AC、AD固定,现已知用去铁丝AC=15米,AD=13米,又测得地面上B、C两点之间距离是9米,B、D两点之间距离是5米,则电线杆和地面是否垂直,为什么?
【变式7-3】(2023春·八年级课时练习)海面上有两个疑似漂浮目标.A舰艇以12海里/时的速度离开港口O,向北偏西50°方向航行;同时,B舰艇在同地以16海里/时的速度向北偏东一定角度的航向行驶,如图所示,离开港口5小时后两船相距100海里,则B舰艇的航行方向是______.
【题型8 勾股定理及其逆定理的综合】
【例8】(2023春·全国·八年级期末)如图,在△ABC中,D是△ABC内一点,连接AD、BD,且AD⊥BD.已知AD=4,BD=3,AC=13,BC=12.则图中阴影部分的面积为________.
【变式8-1】(2023春·江西赣州·八年级期中)如图,已知正方形ABCD的边长为4,E为AB中点,F为AD上的一点,且AF=14AB,求证:∠FEC=90°.
【变式8-2】(2023春·重庆九龙坡·八年级重庆实验外国语学校校考阶段练习)为迎接六十周年校庆,重庆外国语学校准备将一块三角形空地ABC进行新的规划,如图,点D是BC边上的一点,过点D作垂直于AC的小路DE,点E在AC边上.经测量,AB=26米,AD=24米,BD=10米,AC比DC长12米.
(1)求△ABD的面积;
(2)求小路DE的长.
【变式8-3】(2023春·江苏宿迁·八年级校考期末)如图,已知正方形OABC的边长为8,边OA在x轴上,边OC在y轴上,点D是x轴上一点,坐标为(2,0),点E为OC的中点,连接BD、BE、ED.
(1)求点B的坐标;
(2)判断△BED的形状,并证明你的结论.m
2
3
3
4
4
…
n
1
1
2
1
2
…
a
22+12
32+12
32+22
42+12
42+22
…
b
4
6
12
8
16
…
c
22-12
32-12
32-22
42-12
42-22
…
数学八年级上册第六章 一次函数6.1 函数课后复习题: 这是一份数学八年级上册<a href="/sx/tb_c100319_t7/?tag_id=28" target="_blank">第六章 一次函数6.1 函数课后复习题</a>,共13页。
初中数学苏科版八年级上册4.3 实数当堂达标检测题: 这是一份初中数学苏科版八年级上册<a href="/sx/tb_c100311_t7/?tag_id=28" target="_blank">4.3 实数当堂达标检测题</a>,共10页。
初中数学苏科版八年级上册4.3 实数课时练习: 这是一份初中数学苏科版八年级上册<a href="/sx/tb_c100311_t7/?tag_id=28" target="_blank">4.3 实数课时练习</a>,共6页。













