【开学考】2024秋高二上册开学摸底考试卷数学（浙江专用）.zip

这是一份【开学考】2024秋高二上册开学摸底考试卷数学（浙江专用）.zip，文件包含数学解析版docx、数学答案及评分标准docx、数学考试版docx、数学答题卡docx等4份试卷配套教学资源，其中试卷共24页， 欢迎下载使用。

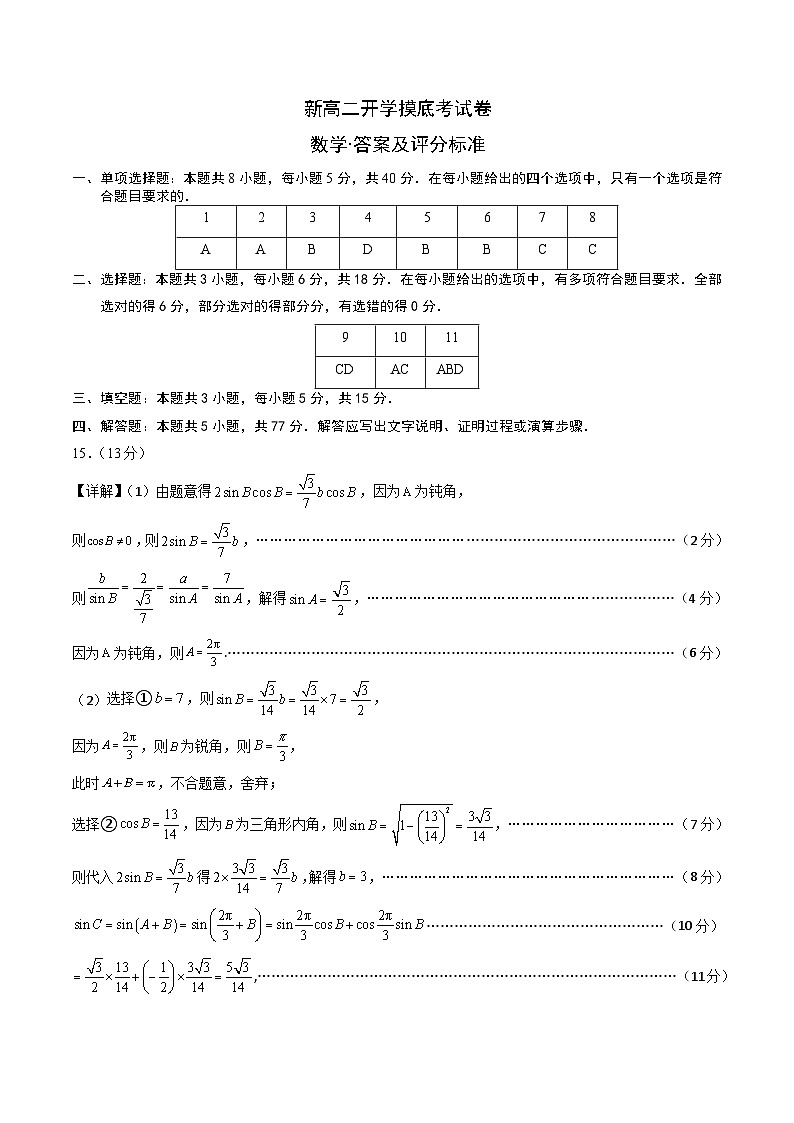
一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个选项是符合题目要求的．
二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．
三、填空题：本题共3小题，每小题5分，共15分．
四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．
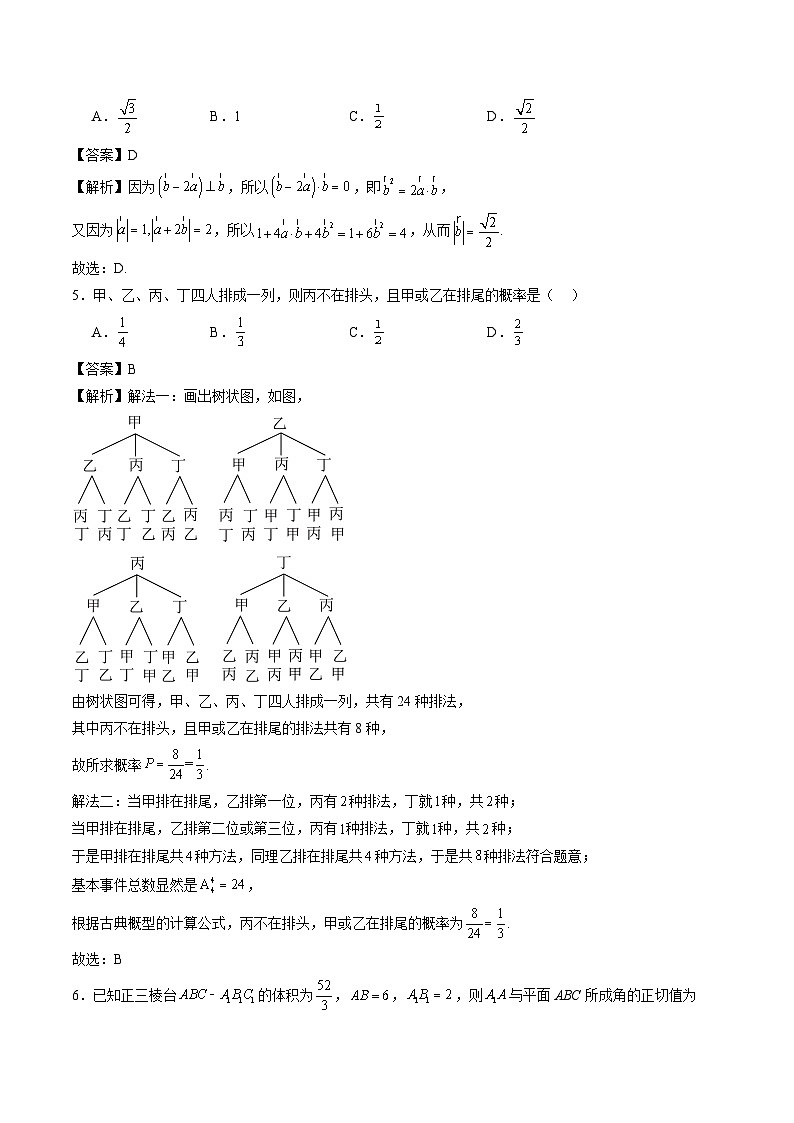
15．（13分）
【详解】（1）由题意得，因为为钝角，
则，则，………………………………………………………………………………（2分）
则，解得，…………………………………………………………（4分）
因为为钝角，则.……………………………………………………………………………………（6分）
选择①，则，
因为，则为锐角，则，
此时，不合题意，舍弃；
选择②，因为为三角形内角，则，………………………………（7分）
则代入得，解得，………………………………………………………（8分）
……………………………………………（10分）
,………………………………………………………………………………（11分）
则.………………………………………………………………（13分）
选择③，则有，解得，…………………………………………………（7分）
则由正弦定理得，即，解得，………………………………………（8分）
因为为三角形内角，则，………………………………………………………（9分）
则…………………………………………（10分）
，……………………………………………………………………………（11分）
则………………………………………………………………（13分）
16．（15分）
【解析】（1）记事件甲连胜四场，则；……………………………………………（4分）
（2）记事件为甲输，事件为乙输，事件为丙输，…………………………………………………（5分）
则四局内结束比赛的概率为
，………………………………………（8分）
所以，需要进行第五场比赛的概率为；……………………………………………………（10分）
（3）记事件为甲输，事件为乙输，事件为丙输，
记事件甲赢，记事件丙赢，…………………………………………………………………………（11分）
则甲赢的基本事件包括：、、、
、、、、，……………………………………………………（13分）
所以，甲赢的概率为.………………………………………………………（14分）
由对称性可知，乙赢的概率和甲赢的概率相等，
所以丙赢的概率为.…………………………………………………………………（15分）
17．（15分）
【解析】（1）由辅助角公式得，……………………………………（2分）
则，………………（6分）
所以该函数的最小正周期;………………………………………………………………………（7分）
（2）由题意，…………………………（8分）
……………………………………………………（9分）
，…………………………（12分）
由可得，………………………………………………………………………（13分）
所以当即时，函数取最大值.……………………………………………………（15分）
18．（17分）
【详解】（1）因为为的中点，所以，………………（2分）
四边形为平行四边形，所以，……………………………………………………………（4分）
又因为平面，平面，………………………………………………………………（5分）
所以平面；…………………………………………………………………………………………（6分）
（2）如图所示，作交于，连接，
因为四边形为等腰梯形，，所以，
结合（1）为平行四边形，可得，又，
所以为等边三角形，为中点，所以，
又因为四边形为等腰梯形，为中点，所以，
四边形为平行四边形，，
所以为等腰三角形，与底边上中点重合，
，，………………………………………………………………………（8分）
因为，所以，所以互相垂直，……………………………………（9分）
以方向为轴，方向为轴，方向为轴，建立空间直角坐标系，………………（10分）
，，，，…（11分）
设平面的法向量为，
则，即，令，得，即，…………………（13分）
设平面的法向量为，
则，即，令，得，即，………（14分），………………………………………………………………………（15分）
则，…………………………………………………………………………………………（16分）
故二面角的正弦值为.……………………………………………………………………（17分）
19．（17分）
【详解】（1）由已知，得，………………………………………………………………（1分）
所以，即，……………………………………………（2分）
又，所以，………………………………………………………………………………（3分）
所以；………………………………………………………………………（5分）
（2）①设，则，…………………………………（6分）
所以，………………………………………………………………（7分）
，………………………（8分）
所以，…………………………………………………………………………（9分）
②，
所以；……………………………………………………………………………（10分）
（3）由（2）得，
故，……………………………………………………………（12分）
………………………………（13分）
，………………………………………………………………………………（14分）
当且仅当，即时等号成立，…………………………………………………（16分）
所以的最小值是9．……………………………………………………………………………………（17分）
1
2
3
4
5
6
7
8
A
A
B
D
B
B
C
C
9
10
11
CD
AC
ABD