






所属成套资源:【开学考】2024年新高二数学开学摸底考试卷(多地区、多版本)
【开学考】2024秋高二上册开学摸底考试卷数学(福建专用).zip
展开
这是一份【开学考】2024秋高二上册开学摸底考试卷数学(福建专用).zip,文件包含数学福建专用解析版docx、数学福建专用答案及评分标准docx、数学福建专用考试版docx等3份试卷配套教学资源,其中试卷共25页, 欢迎下载使用。
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试范围:
4.考试结束后,将本试卷和答题卡一并交回。
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(23-24高一下·甘肃兰州·期末)设集合,,则( )
A.B.C.D.
【答案】B
【分析】根据交集的定义直接求解即可.
【详解】因为,,
所以.
故选:B
2.(23-24高一下·云南·期末)如图,在中,若为上一点,且满足,则( )
A.B.C.D.
【答案】A
【分析】利用将用表示,由共线定理推论即可求得.
【详解】因为所以
由,
因三点共线,由共线定理推论可得,解得
故选:A.
3.(23-24高一下·河南许昌·期末)有一组样本数据如下:56,62,63,63,65,67,68,69,71,74,76,76,77,78,79,79,80,85,87,88,95,98,则其分位数与分位数的和为( )
A.144B.145C.146D.147
【答案】D
【分析】由百分位数的定义求解即可.
【详解】因为,所以样本数据的25%分位数为第六个数据即67;
因为,所以样本数据的75%分位数为第十七个数据即80.
所以25%分位数与75%分位数的和为.
故选:D.
4.(23-24高二下·安徽宣城·期末)已知角的终边过点,则( )
A.B.C.D.1
【答案】D
【分析】根据三角函数的定义求出,对已知进行弦化切,即可求出答案.
【详解】因为角的终边过点,
所以,
所以.
故选:D
5.(23-24高一上·云南曲靖·期末)若定义在上的偶函数在上单调递减,且,则满足的的取值范围是( )
A.B.
C.D.
【答案】B
【分析】根据函数的奇偶性以及单调性,判断函数值的正负情况,由结合函数的性质列出不等式组,可求得答案.
【详解】因为定义域为的偶函数在内单调递减,且,
所以在上单调递增,且,
所以当时,,当时,,
所以由可得或或或,
所以得或或,
所以满足的的取值范围是.
故选:B.
6.(23-24高一下·福建福州·期末)如图,圆锥底面半径为,母线,点为的中点,一只蚂蚁从点出发,沿圆锥侧面绕行一周,到达点,其最短路线长度和其中下坡路段长分别为( )
A.B.C.D.
【答案】D
【分析】将圆锥侧面沿母线剪开并展开成扇形,最短路线即为扇形中的直线段,利用余弦定理即可求解,过作的垂线,垂足为,由题意得到为上坡路段,为下坡路段,计算即可.
【详解】如图,将圆锥侧面沿母线剪开并展开成扇形,
由题可得该扇形半径,弧长为,故圆心角,
最短路线即为扇形中的直线段,由余弦定理可得:;,
过作的垂线,垂足为,当蚂蚁从点爬行到点过程中,它与点的距离越来越小,故为上坡路段,当蚂蚁从点爬行到点的过程中,它与点的距离越来越大,故为下坡路段,下坡路段长,
故选:D
7.(23-24高二下·江西九江·期末)牛顿冷却定律(Newtn's law f cling)是牛顿在1701年用实验确定的:物体在空气中冷却,如果物体的初始温度为,环境温度为,则分钟后物体的温度(单位:)满足:.已知环境温度为,一块面包从温度为的烤箱里拿出,经过10分钟温度降为,那么大约再经过多长时间,温度降为?(参考数据:)( )
A.33分钟B.28分钟C.23分钟D.18分钟
【答案】C
【分析】根据题意列出方程,指数对数互化,解出即可.
【详解】解:依题意,得,
化简得,解得.
设这块面包总共经过分钟,温度降为30°,
则,化简得,
解得,
故大约再经过(分钟),这块面包温度降为30°,
故选:C.
8.(23-24高一下·湖南·期末)冰雹猜想又称考拉兹猜想、角谷猜想、猜想等,其描述为:任一正整数,如果是奇数就乘以3再加1,如果是偶数就除以2,反复计算,最终都将会得到数字1.例如:给出正整数5,则进行这种反复运算的过程为5→16→8→4→2→1,即按照这种运算规律进行5次运算后得到1.若从正整数6,7,8,9,10中任取2个数按照上述运算规律进行运算,则运算次数均为奇数的概率为( )
A.B.C.D.
【答案】A
【分析】根据题中定义,分别求出正整数6,7,8,9,10按照题中所给运算规律进行运算的次数,最后根据古典概型的概率计算公式进行求解即可.
【详解】按照题中运算规律,正整数6的运算过程为,运算次数为;
正整数7的部分运算过程为,
当运算到10时,运算次数为10,由正整数的运算过程可知,
正整数7总的运算次数为;
正整数8的运算次数为;
正整数9的部分运算过程为,当运算到7时,运算次数为3,
由正整数7的运算过程可知,正整数9总的运算次数为.
正整数10的运算次数为6;
故正整数6,7,8,9,10的运算次数分别为偶数、偶数、奇数、奇数、偶数,
从正整数6,7,8,9,10中任取2个数的方法总数为:
,共种,
其中的运算次数均为奇数的方法总数为:,共种,
故运算次数均为奇数的概率为.
故选:A.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.(23-24高一上·江苏苏州·阶段练习)已知正数a,b,则下列说法正确的是( )
A.的最小值为2B.
C.D.
【答案】BC
【分析】由基本不等式和重要不等式逐一判断选项,讨论等号成立的条件可得结果.
【详解】解:A选项:,当且仅当时等号成立,而,故“等号”不成立,A不正确;
B选项:,当且仅当时等号成立,故B正确;
C选项:,当且仅当时等号成立,故C正确;
D选项:,当且仅当时等号成立,故D不正确;
故选:BC
10.(23-24高一下·江苏无锡·期中)已知,表示直线,,,表示平面,则下列推理不正确的是( )
A.,
B.,,且
C., ,
D.,,
【答案】AB
【分析】对于A,根据直线与直线的位置关系判断;对于B,根据直线与平面的位置关系判断;对于C,根据面面平行的位置关系判断;对于D,根据面面平行的性质定理判断.
【详解】对于A,因为,则可以平行或相交,故A错误;
对于B,因为,则或,或,故B错误;
对于C,因为,则由面面平行的位置关系得,故C正确;
对于D,因为,则由面面平行的性质定理得,故D正确.
故选:AB.
11.(23-24高一下·四川绵阳·期末)记的内角的对边分别为,则( )
A.当时,为直角三角形
B.当时,最大角与最小角之和为
C.当.时,
D.当时,为锐角三角形
【答案】ABC
【分析】根据余弦定理求解长度,即可判断A,根据余弦定理求解中间角,即可求解B,根据正弦定理即可求解C,利用正弦定理边角互化,结合三角恒等变换即可求解D.
【详解】对于A,由余弦定理可得,
由于,故为直角三角形,A正确,
对于B,三角形的三边长分别为,
,,,故,
则该三角形最大角与最小角之和为,B正确,
对于C,由正弦定理可得,由于,故,C正确,
对于D,由可得,
所以,由于,所以,进而,故,因此三角形为钝角三角形,D错误,
故选:ABC
三、填空题:本题共3小题,每小题5分,共15分.
12.(广东省广州市白云区2023-2024学年高一下学期期末数学试题)已知复数z满足,则 .
【答案】/
【分析】先求出复数z,再根据复数的模的定义直接计算即可得解.
【详解】由题意,
故.
故答案为:.
13.(23-24高二下·重庆·阶段练习)若不等式成立的一个充分不必要条件是,则实数的取值范围为 .
【答案】
【分析】根据绝对值不等式的解法,结合充分不必要条件的性质进行求解即可.
【详解】由,
因为不等式成立的一个充分不必要条件是,
所以有,等号不同时成立,,
当时,是不等式成立的充要条件,不符合题意,
所以,实数的取值范围为.
故答案为:.
14.(23-24高一下·重庆万州·期中)一个棱长为2的正四面体盒子内部放置了一个正方体,且该正方体在铁盒内能任意转动,则该正方体棱长的最大值为 .
【答案】/
【分析】将所求问题转化为正方体的外接球,即为正四面体的内切球,作出图形,利用等体积法求得内切球的半径,利用正方体的体对角线等于正方体的外接球的直径即可求解.
【详解】由题意可知,正方体在正四面体内部任意旋转,
当正方体的棱长取得最大值时,正方体的外接球即为正四面体的内切球,
将正四面体放到正方体中,作出图形如图,
因为正四面体的棱长为2,则图中正方体的棱长为,
所以正四面体的体积为,
侧面积为,
设正四面体的内切球的半径为,则,解得,
设放置进去的正方体的棱长最大值为,则,解得.
故答案为:.
四、解答题:本题共5小题,其中第15题13分,第16,17题15分,第18,19题17分,共77分.解答应写出文字说明、证明过程或演算步骤.
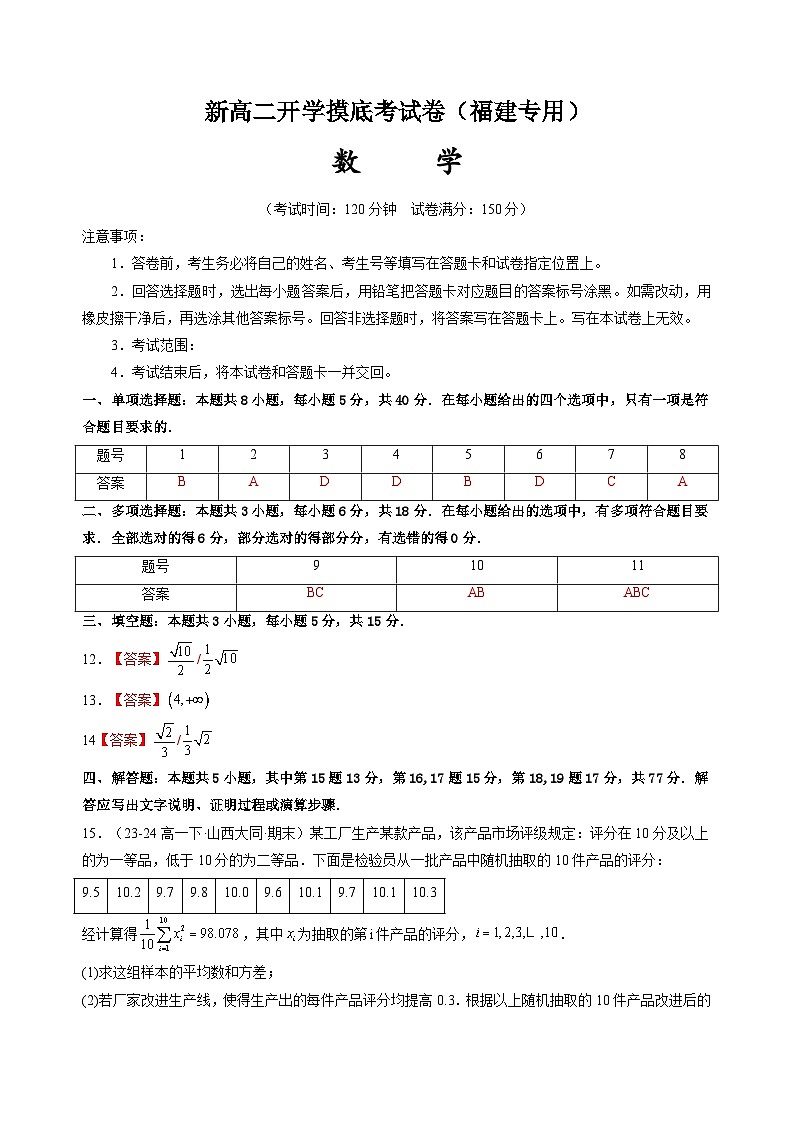
15.(23-24高一下·山西大同·期末)某工厂生产某款产品,该产品市场评级规定:评分在10分及以上的为一等品,低于10分的为二等品.下面是检验员从一批产品中随机抽取的10件产品的评分:
经计算得,其中为抽取的第件产品的评分,.
(1)求这组样本的平均数和方差;
(2)若厂家改进生产线,使得生产出的每件产品评分均提高0.3.根据以上随机抽取的10件产品改进后的评分,估计改进后该厂生产的产品评分的平均数和方差.
【答案】(1)样本平均数为,样本方差为.
(2)平均数为,方差为
【分析】(1)根据题意,由平均数以及方差的计算公式代入计算,即可求解;
(2)根据题意,由平均数与方差的性质即可得到结果.
【详解】(1)样本平均数为.
样本方差为.
(2)因为改进后随机抽取的10件产品的评分是改进前抽取的10件产品的评分每个提高0.3分,所以改进后生产的产品评分的平均数,
方差为.
16.(23-24高一下·湖南株洲·期末)小米在2024年推出SU7汽车,创始人雷军为了了解广大客户对小米SU7的评价,令销售部随机抽取200名客户进行了问卷调查,根据统计情况,将他们的年龄按,,,分组,并绘制出了如图所示的频率分布直方图.
(1)估计样本数据中用户年龄的众数与平均数(同一组中的数据用该组区间的中点值作代表);
(2)销售部从年龄在,内的样本中按比例分配的分层随机抽样方法抽取6人,再从这6人中随机抽取2人进行电话回访,求这2人取自不同年龄区间的概率.
【答案】(1)平均数为44.5,众数为45.
(2).,
【分析】(1)根据频率分步直方图易知众数,由平均数计算公式可得结果;
(2)由抽样比可确定每层中的抽样人数,再由古典概率计算公式可得结果
【详解】(1)由平均数计算公式,可估计平均数为,
根据频率分步直方图,估计众数为45.
(2)由已知可得抽取的6人中,年龄在内的有4人,分别记为;
年龄在内的有2人,分别记为;
则从这6人中随机抽取2人的样本点为
,,,,,,,,,
,,,,,,共15个;
记事件“这2人取自不同年龄区间”,其包含样本点有,,,,
,,,,共8个,
故这2人取自不同年龄区间的概率为.
17.(23-24高一下·上海宝山·期末)锐角中角、、的对边分别为、、,且.
(1)求角的大小;
(2)若,求的取值范围.
【答案】(1)
(2)
【分析】(1)借助正弦定理将角化为边后,借助余弦定理计算即可得;
(2)借助正弦定理将边化为角后,结合两角和的正弦公式与辅助角公式可将化为正弦型函数形式,再利用锐角三角形性质可得角的范围,即可得解.
【详解】(1)由正弦定理可得,即,
由余弦定理可得,又,则;
(2)由,则、,
则
,
由为锐角三角形,可得,解得,
则,则,
故.
18.(23-24高一上·江西鹰潭·期末)已知函数(),其相邻两个对称中心之间的距离为.
(1)求实数的值及函数的单调递增区间;
(2)将图象上所有点向平左移个单位长度,再将图象上所有点向上平移1个单位,得到函数的图象,若在上有两个不同零点,求实数的取值范围.
【答案】(1),单调递增区间是();
(2).
【分析】(1)利用三角恒等变换得,再由相邻两个对称中心之间的距离为,可求得,即,再根据正弦函数的单调性即可求解;
(2)由三角函数的图象变换可得,然后将的零点问题转化为直线与函数在的图象的交点个数问题,再结合几何图形求出实数的取值范围.
【详解】(1)依题意,
因为相邻两个对称中心之间的距离为,
所以的周期,解得,
所以,
由,,
得,
所以单调递增区间为.
(2)由,可得,
由,,
得,,
所以函数在上单调递增,在上单调递减,
所以函数在的图象如图所示:
因为在上有两个不同零点,
即直线与函数在的图象有两个交点,此时,
所以实数的取值范围是.
19.(23-24高一下·广东广州·期中)若是定义在上的增函数,其中,存在函数,,且函数图像上存在两点,图像上存在两点,其中两点横坐标相等,两点横坐标相等,且,则称在上可以对进行“型平行追逐”,即是在上的“型平行追逐函数”. 已知是定义在上的奇函数,是定义在上的偶函数.
(1)求满足的的值;
(2)设函数,若不等式对任意的恒成立,求实数的取值范围;
(3)若函数是在上的“型平行追逐函数”,求正数的取值范围.
【答案】(1)
(2)
(3)
【分析】(1)先确定的表达式,再解方程得到结果;
(2)计算的表达式,然后对分类讨论即可;
(3)将命题转化为在上不是单调函数,再通过对换元并分析单调性得到答案.
【详解】(1)由于是奇函数,故,即恒成立,所以;
由于是偶函数,故,即恒成立,所以.
故,.
现要解方程,而,故命题等价于,即.
这是关于正实数的二次方程,解得,所以.
(2)由于,
而单调递增,且对有,故当时,的取值范围是.
从而命题等价于对任意的,有,即.
若,则有,故条件对不成立,不符合要求;
若,则对有,符合要求.
所以的取值范围是.
(3)我们有,.
根据题目定义,是在上的“型平行追逐函数”,当且仅当存在,满足.
换言之,函数在上不是单调函数.
由于
,
而在上递增,取值范围为.
故命题等价于在上不是单调函数.
对,我们知道在上递减,在上递增.
所以命题等价于,从而正数的取值范围是.
【点睛】关键点点睛:本题的关键点在于对型函数的单调性的反复运用.
9.5
10.2
9.7
9.8
10.0
9.6
10.1
9.7
10.1
10.3
相关试卷
这是一份【开学考】2024秋高二上册开学摸底考试卷数学(辽宁专用).zip,文件包含数学辽宁专用解析版docx、数学辽宁专用考试版docx、数学辽宁专用答案及评分标准docx、数学辽宁专用答题卡docx等4份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。
这是一份【开学考】2024秋高二上册开学摸底考试卷数学(湖北专用).zip,文件包含新高二数学开学摸底考湖北专用解析版docx、新高二数学开学摸底考湖北专用答案及评分标准docx、新高二数学开学摸底考湖北专用考试版docx、新高二数学开学摸底考湖北专用答题卡docx、新高二数学开学摸底考湖北专用答题卡pdf等5份试卷配套教学资源,其中试卷共34页, 欢迎下载使用。
这是一份【开学考】2024秋高二上册开学摸底考试卷数学(浙江专用).zip,文件包含数学解析版docx、数学答案及评分标准docx、数学考试版docx、数学答题卡docx等4份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。









