湖南省长沙市六校2024届高三下学期联考数学试卷(含答案)

这是一份湖南省长沙市六校2024届高三下学期联考数学试卷(含答案)，共16页。试卷主要包含了选择题，多项选择题，填空题，双空题，解答题等内容，欢迎下载使用。

一、选择题
1．若集合，，则( )
A.B.C.D.
2．已知向量，，且，则实数( )
A.1或4B.1或C.或1D.或1
3．为了得到函数的图象，只要把函数图象上所有的点( )
A.向右平行移动个单位长度B.向左平行移动个单位长度
C.向右平行移动个单位长度D.向左平行移动个单位长度
4．“”是“圆与圆相切”的( )
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件
5．若，且，，则( )
A.B.C.D.
6．若展开式的常数项为60，则a值为( )
A.4B.C.2D.
7．深度学习是人工智能的一种具有代表性的实现方法，它是以神经网络为出发点的，在神经网络优化中，指数衰减的学习率模型为，其中L表示每一轮优化时使用的学习率，表示初始学习率，D表示衰减系数，G表示训练迭代轮数，表示衰减速度.已知某个指数衰减的学习率模型的初始学习率为0.5，衰减速度为18，且当训练迭代轮数为18时，学习率衰减为0.4，则学习率衰减到0.2以下（不含0.2）所需的训练迭代轮数至少为( )（参考数据：）
A.72B.74C.76D.78
8．已知，分别是椭圆（）的左，右焦点，M，N是椭圆C上两点，且，，则椭圆C的离心率为( )
A.B.C.D.
二、多项选择题
9．带有编号1、2、3、4、5的五个球，则( )
A.全部投入4个不同的盒子里，共有种放法
B.放进不同的4个盒子里，每盒至少一个，共有种放法
C.将其中的4个球投入4个盒子里的一个(另一个球不投入)，共有种放法
D.全部投入4个不同的盒子里，没有空盒，共有种不同的放法
10．已知的内角A，B，C的对边分别为a，b，c，，，，则( )
A.B.
C.的面积为D.的周长为
11．已知函数.则下列说法正确的是( )
A.当时，
B.当时，直线与函数的图象相切
C.若函数在区间上单调递增，则
D.若在区间上恒成立，则
三、填空题
12．已知双曲线过点，则其渐近线方程为________.
13．已知复数z满足，则________.
四、双空题
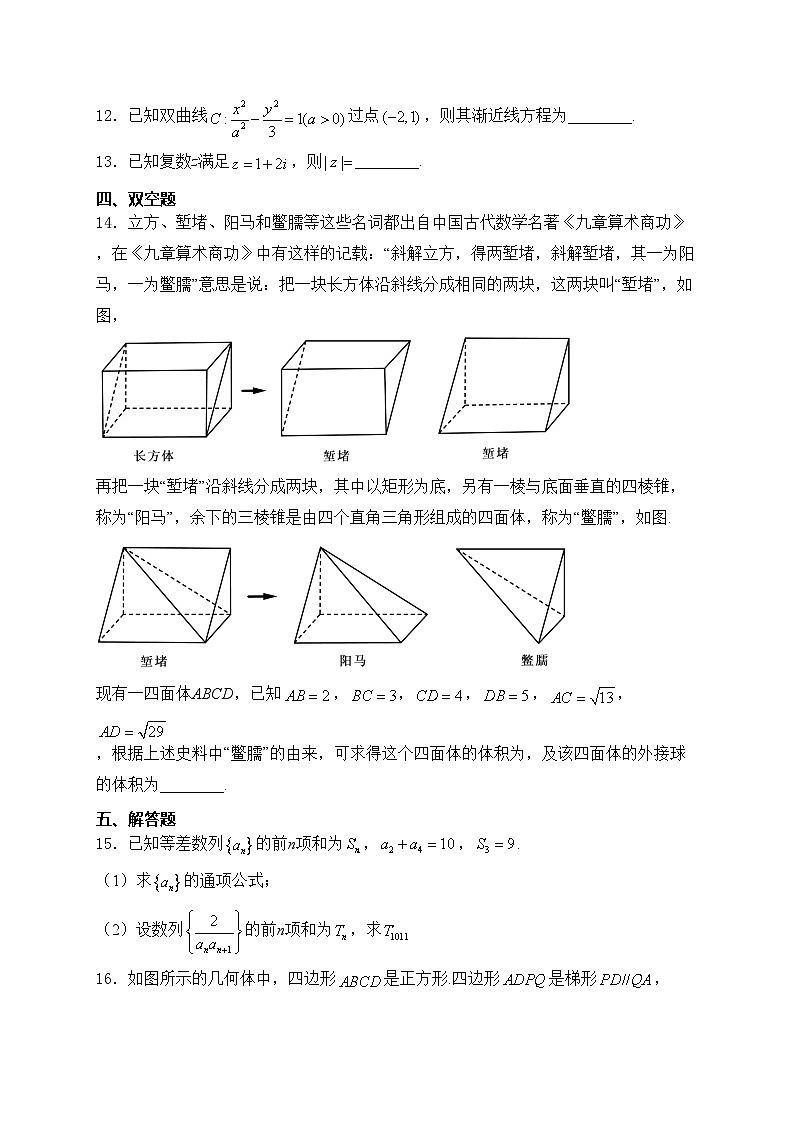
14．立方、堑堵、阳马和鳖臑等这些名词都出自中国古代数学名著《九章算术商功》，在《九章算术商功》中有这样的记载：“斜解立方，得两堑堵，斜解堑堵，其一为阳马，一为鳖臑”意思是说：把一块长方体沿斜线分成相同的两块，这两块叫“堑堵”，如图，
再把一块“堑堵”沿斜线分成两块，其中以矩形为底，另有一棱与底面垂直的四棱锥，称为“阳马”，余下的三棱锥是由四个直角三角形组成的四面体，称为“鳖臑”，如图.
现有一四面体ABCD，已知，，，，，，根据上述史料中“鳖臑”的由来，可求得这个四面体的体积为，及该四面体的外接球的体积为________.
五、解答题
15．已知等差数列的前n项和为，，.
（1）求的通项公式；
（2）设数列的前n项和为，求
16．如图所示的几何体中，四边形是正方形.四边形是梯形，，平面平面，且.
（1）求证：平面；
（2）求二面角的大小.
17．要获得某项英语资格证书必须依次通过听力和笔试两项考试，只有听力成绩合格时，才可继续参加笔试的考试.已知听力和笔试各自允许有一次补考机会，两项成绩均合格方可获得证书.现某同学参加这项证书考试，根据以往模拟情况，听力考试成绩每次合格的概率均为，笔试考试成绩每次合格的概率均为，假设各次考试成绩合格与否均互不影响.
（1）求他不需要补考就可获得证书的概率；
（2）求他恰好补考一次就获得证书的概率；
（3）在这项考试过程中，假设他不放弃所有的考试机会，记他参加考试的次数为，求参加考试次数的分布列和期望值.
18．已知椭圆的离心率为，、分别为椭圆C的左、右顶点，点满足.
（Ⅰ）求椭圆C的方程；
（Ⅱ）设直线l经过点P且与C交于不同的两点M、N，试问：在x轴上是否存在点Q，使得直线与直线的斜率的和为定值？若存在，请求出点Q的坐标及定值；若不存在，请说明理由.
19．已知函数.
（1）当时，求函数的极值；
（2）求函数的单调区间；
（3）当时，若在时恒成立，求整数k的最大值.
参考答案
1．答案：B
解析：，，
则，
故选：B.
2．答案：B
解析：由，，，有，解得.
故选：B
3．答案：C
解析：因为，所以只要把函数图象上所有的点向右平行移动个单位长度，即可得到函数的图象.
故选：C
4．答案：A
解析：圆圆心，半径为；
圆圆心，半径为；
当两圆相切时，可分为内切和外切两种，
圆心距为，
①当两圆外切时：，即.
②当两圆内切时：，即.
则根据充分条件和必要条件的判定原则，
可知“”是“圆与圆相切”的充分不必要条件.
故选：A
5．答案：C
解析：因为，所以，则，
因为，，
所以，，
则.
故选：C.
6．答案：D
解析：因为展开式的通项为，
令，则，所以常数项为，即，所以.
故选D
7．答案：B
解析：由于，所以，
依题意，则，
则，
由，
所以，即，
所以所需的训练迭代轮数至少为74次.
故选：B
8．答案：C
解析：连接，设，则，，，
在中，即，
，，，
，，
在中，，即，
，，又，.
故选：C.
9．答案：ACD
解析：对于A：每个球都可以放入4个不同的盒子，则共有种放法，A正确；
对于B：放进不同的4个盒子里，每盒至少一个，则有：
全部投入4个不同的盒子里，每盒至少一个，相当于把其中的2个球捆绑成一个球，再进行排列，共有种放法，B错误；
对于C：先选择4个球，有种，再选择一个盒子，有种，故共有种放法，C正确；
对于D：全部投入4个不同的盒子里，没有空盒，则相当于把其中的2个球捆绑成一个球，再进行排列，共有种放法，D正确；
故选：ACD.
10．答案：ABD
解析：由，有，得，选项A正确.
因为，由正弦定理有，，得，选项B正确.
的面积为，选项C错误.
因为，由余弦定理，
解得，故的周长为，选项D正确.
故选：ABD
11．答案：AB
解析：对于A，当时，，，
当时，，
当时，，
函数在上单调递减，在上单调递增，
，故选项A正确；
对于B，当时，，，
，
函数在处的切线方程为，故选项B正确；
对于C，，若函数在区间上单调递增，
则区间上恒成立，
即在上恒成立，
令，，
则，
函数在上单调递减，
，
，故选项C错误；
对于D，当时，恒成立，此时；
当时，恒成立等价于恒成立，
即恒成立，
设，，
则在上恒成立，
在上单调递减，
，
，
综上所述，故选项D错误.
故选:AB.
12．答案：
解析：因为双曲线过点，
即有，解得或（舍），而，
故渐近线方程，即.
故答案为：
13．答案：
解析：因为，所以.
故答案为：
14．答案：4；.
解析：根据资料可得“鳖臑”的由来是将长方体分解一半，得到三棱柱，三棱柱再分成两块；现将“鳖臑”还原成长方体，
由已知，，，，，，
还原成长方体，如图，
从还原的长方体可以看出，四面体的体积；
长方体的体对角线即为四面体的外接球的直径，
四面体的外接球的体积.
故答案为4；.
15．答案：（1）；
（2）
解析：（1）因为是等差数列，可设首项为，公差为d，
由题意得：，
，
联立解得：，，
是首项为1，公差为2的等差数列，通项公式为.
（2）由上问可知，数列是公差为2的等差数列，通项公式.
所以，
从而可得，
从而可得，
.
16．答案：（1）证明见解析；
（2）.
解析：（1），平面，
平面
，平面，平面，
平面
，平面
平面平面
平面，
平面
（2）以D为原点，分别以、、所在直线为x轴、y轴、z轴，建立空间直角坐标系，
设，则，，，
设平面一个法向量，，
则，即，
令，则，，
设平面一个法向量，，
则，即，
令，则，，
，
，
设二面角的平面角为，
则，
故
17．答案：（1）；
（2）；
（3）分布列见解析；期望为
解析：（1）设“听力第一次考试合格”为事件，“听力补考合格”为事件；“笔试第一次考试合格”为事件，“笔试补考合格”为事件
不需要补考就获得证书的事件为，注意到与相互独立，
则
（2）恰好补考一次的事件是
则；
（3）由已知得，，
注意到各事件之间的独立性与互斥性，可得
，
，
，
参加考试次数的期望值，
18．答案：（1）；
（2），定值为1.
解析：（Ⅰ）依题意得，，，
，
解得.
，，，
故椭圆C的方程为.
(II)假设存在满足条件的点.
当直线l与x轴垂直时，它与椭圆只有一个交点，不满足题意.
因此直线l的斜率k存在，设直线l的方程为，
由消去y整理得，
设、，
则，，
，
要使对任意实数k，为定值，则只有，
此时.
故在x轴上存在点，使得直线与直线的斜率的和为定值1.
19．答案：（1）在处取得极大值，无极小值；
（2）当时，在上单调递增，
当时，在上单调递增，上单调递减；
（3）整数k的最大值为5
解析：（1）当时，，
所以，
当时，，单调递增，
当时，，单调递减，
所以在处取得极大值，无极小值.
（2），
当时，恒成立，所以在上单调递增，
当时，当时，，所以在上单调递增，
当时，，所以在上单调递减，
综上所述：当时，在上单调递增，
当时，在上单调递增，上单调递减.
（3）在时恒成立，即恒成立，
令，则，
令，则在上恒成立，
所以在上单调递增，且
，所以在存在唯一实数，
使得，即，所以
当时，，即，
当时，，即，
所以在上单调递减，上单调递增，
所以，
故，又，整数k的最大值为5.