江苏省南通市2023-2024学年高二下学期5月期中质量监测数学试卷(含答案)

这是一份江苏省南通市2023-2024学年高二下学期5月期中质量监测数学试卷(含答案)，共15页。试卷主要包含了选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。

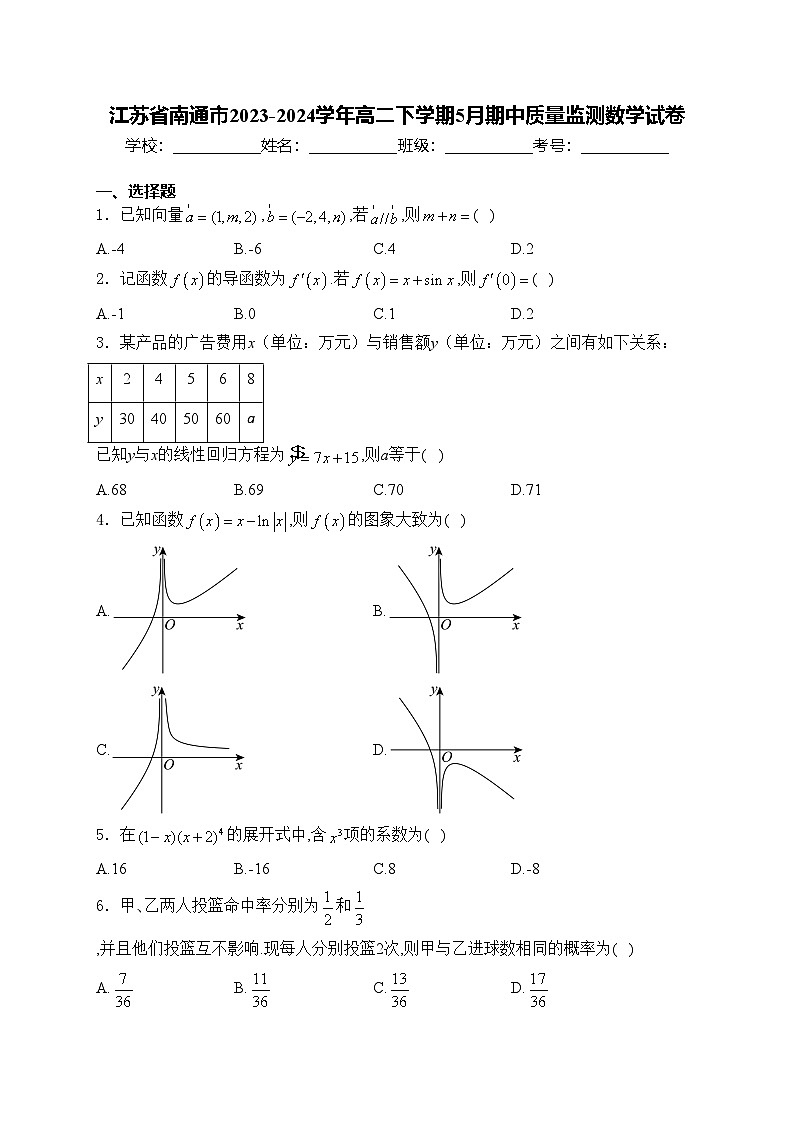
一、选择题
1．已知向量,,若,则( )
A.-4B.-6C.4D.2
2．记函数的导函数为.若,则( )
A.-1B.0C.1D.2
3．某产品的广告费用x（单位：万元）与销售额y（单位：万元）之间有如下关系：
已知y与x的线性回归方程为,则a等于( )
A.68B.69C.70D.71
4．已知函数,则的图象大致为( )
A.B.
C.D.
5．在的展开式中,含项的系数为( )
A.16B.-16C.8D.-8
6．甲､乙两人投篮命中率分别为和,并且他们投篮互不影响.现每人分别投篮2次,则甲与乙进球数相同的概率为( )
A.B.C.D.
7．今年春节,《热辣滚汤》､《飞驰人生2》､《熊出没之逆转时空》､《第二十条》引爆了电影市场,小帅和他的同学一行四人决定去看电影.若小帅要看《飞驰人生2》,其他同学任选一部,则恰有两人看同一部影片的概率为( )
A.B.C.D.
8．已知函数,若对任意正数,,都有恒成立,则实数a的取值范围( )
A.B.C.D.
二、多项选择题
9．有3名学生和2名教师排成一排,则下列说法正确的是( )
A.共有120种不同的排法
B.当2名教师相邻时,共有24种不同的排法
C.当2名教师不相邻时,共有72种不同的排法
D.当2名教师不排在两端时,共有48种不同的排法
10．已知,则( )
A.展开式各项的二项式系数的和为
B.展开式各项的系数的和为
C.
D.
11．如图所示的空间几何体是由高度相等的半个圆柱和直三棱柱组合而成,,,G是上的动点.则( )
A.平面平面
B.G为的中点时,
C.存在点G,使得直线与的距离为
D.存在点G,使得直线与平面所成的角为
三、填空题
12．已知随机变量,且,则_______________.
13．已知事件A,B相互独立.若,则_______________.
14．若函数有绝对值不大于1的零点,则实数a的取值范围是______________.
四、解答题
15．已知函数.
(1)求曲线在处的切线方程;
(2)求在上的最值.
16．如图,在直四棱柱中,底面是梯形,,且,E是的中点.
(1)求点C到平面的距离;
(2)求二面角的正弦值.
17．“五一”假期期间是旅游的旺季,某旅游景区为了解不同年龄游客对景区的总体满意度,随机抽取了“五一”当天进入景区的青､老年游客各120名进行调查,得到下表：
(1)依据小概率值的独立性检验,能否认为“是否满意”与“游客年龄”有关联;
(2)若用频率估计概率,从“五一”当天进入景区的所有游客中任取3人,记其中对景区不满意的人数为X,求X的分布列与数学期望.
附：,其中.
18．已知函数,.
(1)讨论的单调性;
(2)当时,证明：;
(3)若函数有两个极值点,,求的取值范围.
19．现有外表相同,编号依次为的袋子,里面均装有n个除颜色外其他无区别的小球,第个袋中有k个红球,个白球.随机选择其中一个袋子,并从中依次不放回取出三个球.
(1)当时,
①假设已知选中的恰为2号袋子,求第三次取出的是白球的概率;
②求在第三次取出的是白球的条件下,恰好选的是3号袋子的概率;
(2)记第三次取到白球的概率为p,证明：.
参考答案
1．答案：B
解析：由,知,使得,
即,所以,
解得,所以.
故选：B.
2．答案：D
解析：,
所以.
故选：D.
3．答案：C
解析：由题意可知,,
因为线性回归方程过样本中心点,
所以,
所以,
解得.
故选：C.
4．答案：A
解析：函数的定义域为,
当时,,
因为函数在上都是增函数,
所以函数在上是增函数,
当时,,则,
当时,,当时,,
所以函数在上单调递减,在上单调递增,
综上所述,的增区间为,,减区间为,
则A选项符合题意.
故选：A.
5．答案：B
解析：由题意所求系数为：.
故选：B.
6．答案：C
解析：甲与乙两个进球数都为0的概率为：,
甲与乙两个进球数都为1的概率为：,
甲与乙两个进球数都为2的概率为：,
所以甲与乙进球数相同的概率,
故选：C.
7．答案：B
解析：分两种情况讨论：
(1)小帅和其中一个同学同时看《飞驰人生2》,另外两个看剩余三部电影中的两部,此时所求概率为：;
(2)观看《飞驰人生2》只有小帅一人,只需要将剩余三人分成两组,再将这两组人分配给两部电影,此时所求概率为：;
综上,恰有两人看同一部影片的概率;
故选：B.
8．答案：C
解析：不妨令,
则,
即在单调递增,
因为,
则在上恒成立,
即,在上恒成立,
则,
又,
.
故选：C.
9．答案：AC
解析：对于A,共有种不同的排法,故A正确;
对于B,共有种不同的排法,故B错误;
对于C,共有种不同的排法,故C正确;
对于D,共有种不同的排法,故D错误.
故选：AC.
10．答案：AC
解析：对于A,的展开式各项的二项式系数的和为,A正确;
对于B,令,得,即的展开式各项的系数的和为1,B错误;
对于C,令,得,则,
,即有,C正确;
对于D,对两边求导,
得,
令,得,D错误.
故选：AC.
11．答案：AB
解析：对于选项A,由题意知,,平面,
因为平面,所以,
又,、平面,
所以平面,
因为平面,所以平面平面,即选项A正确;
对于选项B,当G为的中点时,取的中点H,连接,,
则,,所以四边形是平行四边形,
所以,
因为和都是等腰直角三角形,所以,
所以,所以,即选项B正确;
对于选项C,因为,且平面,平面,
所以平面,
所以直线与的距离等价于直线到平面的距离,
也等价于点F到平面的距离,
以A为坐标原点,,,所在直线分别为x,y,z轴建立如图所示的空间直角坐标系,
则 ,,,
设点,其中,,
由射影定理知,,即,
所以,,,
设平面的法向量为,则,
取,则,,所以,
若直线与的距离为,则点到平面的距离为,
而点F到平面的距离,
所以不存在点G,使得直线与的距离为,即选项C错误;
对于选项D,,,
所以,,,
设平面的法向量为,则,
取,则,,所以,
若直线与平面所成的角为,
则,
由,知,
代入上式整理得,此方程无解,
所以不存在点G,使得直线与平面所成的角为,即选项D错误.
故选：AB.
12．答案：0.2
解析：因为随机变量,且,
所以.
故答案为：0.2.
13．答案：0.12
解析：因为事件A,B相互独立,
所以事件,B相互独立,
所以,
所以.
故答案为：0.12.
14．答案：
解析：令,得,
因为函数有绝对值不大于1的零点,
所以方程有绝对值不大于1的解,
令,,则,
令,得,令,得或,
所以函数在上单调递增,在,上单调递减,
又,,,
所以,
所以.
故答案为：.
15．答案：(1);
(2),.
解析：(1)函数,求导得,则,而,
所以曲线在处的切线方程为,即.
(2)由(1)知,当时,,当时,,
函数在上单调递减,在上单调递增,而,,
所以当时,函数取得最大值,
当时,函数取得最小值,
16．答案：(1);
(2).
解析：(1)在直四棱柱中,,则直线,,两两垂直,
以D为原点,直线,,分别为x,y,z轴建立空间直角坐标系,
而,且,E是的中点,
则,,,,,
,,,,
设平面的法向量,则,令,得,
所以点C到平面的距离.
(2)设平面的法向量,则,令,得,
设二面角的大小为,则,
所以二面角的正弦值
17．答案：(1)能认为有关
(2)分布列见解析,
解析：(1)零假设“是否满意”与“游客年龄”没有关联,
,
所以依据小概率值的独立性检验,可以推断零假设不成立,
即能认为“是否满意”与“游客年龄”有关联;
(2)由题意,任抽取1人不满意的概率为,
则,
所以,
,
,
,
所以X的分布列为：
所以.
18．答案：(1)答案见解析;
(2)证明见解析;
(3).
解析：(1)函数的定义域为,
求导得,
当时,,函数在上单调递减,
当时,由,得,由,得,
则函数在上单调递减,在上单调递增,
所以当时,函数的递减区间是,无递增区间;
当时,函数的递减区间是,递增区间是.
(2)由(1)知,当时,函数在取得最小值,
要证,只需证明,
令,求导得,当时,,当时,,
则函数在上单调递减,在上单调递增,,,
所以当时,,即成立.
(3)函数的定义域为,求导得,
由函数有两个极值点,,得方程在上有两个不等实根,
设,对称轴为,,
则,,且,,
即;
,
令,由,得,即,解得,
令,,求导得,
因此函数在上单调递减,,即,
所以的取值范围是.
19．答案：(1)①;②
(2)证明见解析
解析：(1)①时,第二个袋中有2白2红,共4个球,
从中连续取出三个球（每个取后不放回）,
第三次取出为白球的情况有：红红白,红白白,白红白,
第三次取出为白球的概率为;
②设选出的是第个袋,连续三次取球的方法数为,
第三次取出的是白球的三次取球颜色有如下四种情形：
（白,白,白）,若则,取法数为,
若或或,取法数为0,也满足关系,
故取（白,白,白）的取法可表示为,
同理（白,红,白）,取法数为,
（红,白,白）,取法数为,
（红,红,白）,取法数为,
从而第三次取出的是白球的种数为：
,
则在第k个袋子中第三次取出的是白球的概率,
则在第3个袋子中第三次取出的是白球的概率,
而选到第k个袋子的概率为,故所求概率为：
,
所以在第三次取出的是白球的条件下,恰好选的是3号袋子的概率为;
(2)设选出的是第k个袋,连续三次取球的方法数为,
第三次取出的是白球的三次取球颜色有如下四种情形：
（白,白,白）,取法数为,
（白,红,白）,取法数为,
（红,白,白）,取法数为,
（红,红,白）,取法数为,
从而第三次取出的是白球的种数为：
,
则在第k个袋子中第三次取出的是白球的概率,
而选到第k个袋子的概率为,
所以.
x
2
4
5
6
8
y
30
40
50
60
a
满意
不满意
青年
80
40
老年
100
20
0.10
0.05
0.010
0.005
0.001
2.706
3.841
6.635
7.879
10.828
X
0
1
2
3
P