重庆市璧山区青杠初级中学2023年数学八上期末考试试题【含解析】

这是一份重庆市璧山区青杠初级中学2023年数学八上期末考试试题【含解析】，共17页。试卷主要包含了考生要认真填写考场号和座位序号，点的位置在等内容，欢迎下载使用。
1．考生要认真填写考场号和座位序号。
2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。
3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。
一、选择题（每题4分，共48分）
1．如图，AB=AC，CF⊥AB于F，BE⊥AC于E，CF与BE交于点D．有下列结论：
①△ABE≌△ACF；②△BDF≌△CDE；③点D在∠BAC的平分线上；④点C在AB的中垂线上．以上结论正确的有（ ）个．
A．1B．2C．3D．4
2．如图，AE垂直于∠ABC的平分线交于点D，交BC于点E，CE=BC，若△ABC的面积为2，则△CDE的面积为（ ）
A．B．C．D．
3．4 的算术平方根是
A．16B．2C．-2D．
4．点的位置在
A．第一象限B．第二象限C．第三象限D．第四象限
5．图中的小正方形边长都相等，若，则点Q可能是图中的（ ）
A．点DB．点CC．点BD．点A
6．两千多年前，古希腊数学家欧几里得首次运用某种数学思想整理了几何知识，完成 了数学著作《原本》，欧几里得首次运用的这种数学思想是（ ）
A．公理化思想B．数形结合思想C．抽象思想D．模型思想
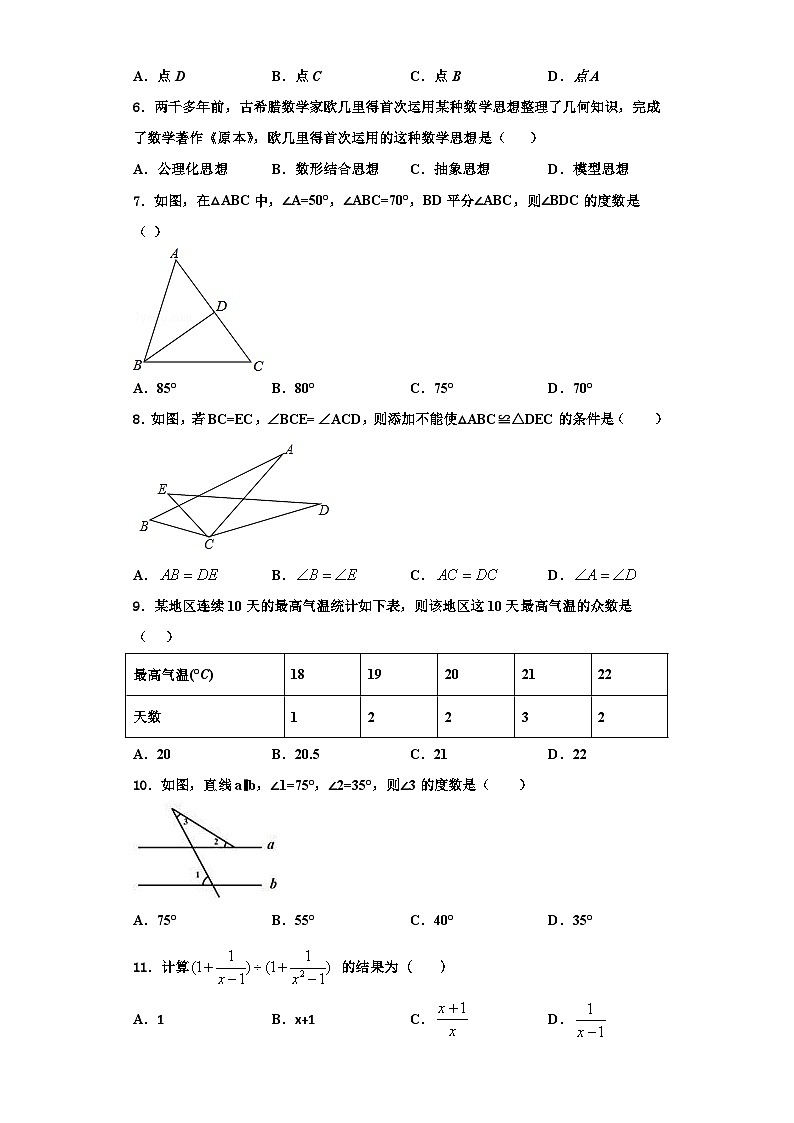
7．如图，在△ABC中，∠A=50°，∠ABC=70°，BD平分∠ABC，则∠BDC的度数是（ ）
A．85°B．80°C．75°D．70°
8．如图，若BC=EC，∠BCE=∠ACD，则添加不能使△ABC≌△DEC的条件是（ ）

A．B．C．D．
9．某地区连续10天的最高气温统计如下表，则该地区这10天最高气温的众数是（ ）
A．20B．20.5C．21D．22
10．如图，直线a∥b，∠1=75°，∠2=35°，则∠3的度数是（ ）
A．75°B．55°C．40°D．35°
11．计算 的结果为（ ）
A．1B．x+1C．D．
12．若代数式有意义，则实数的取值范围是 （ ）
A．B．C．D．
二、填空题（每题4分，共24分）
13．已知线段AB//x轴,且AB=3，若点A的坐标为(-1,2),则点B的坐标为_______;
14．如图，两个三角形全等，则∠α的度数是____
15．已知CD是Rt△ABC的斜边AB上的中线，若∠A＝35°，则∠BCD＝_____________．
16． “同位角相等”的逆命题是__________________________．
17．已知直线AB的解析式为：y=kx+m，且经过点A（a，a），B（b，8b）（a＞0，b＞0）．当是整数时，满足条件的整数k的值为 ．
18．甲、乙俩射击运动员进行10次射击，甲的成绩是7，7，8，9，8，9，10，9，9，9，乙的成绩如图所示．则甲、乙射击成绩的方差之间关系是 （填“＜”，“=”，“＞”）．
三、解答题（共78分）
19．（8分）先化简代数式： ，然后再从﹣2≤x≤2的范围内选取一个合适的整数代入求值．
20．（8分）（1）如图1，求证：
（ 图1）
（2）如图2，是等边三角形，为三角形外一点，，求证：
（ 图2）
21．（8分）直角坐标系中，A，B，P的位置如图所示，按要求完成下列各题：
（1）将线段AB向左平移5个单位，再向下平移1个单位，画出平移后的线段A1B1；
（2）将线段AB绕点P顺时针旋转90°，画出旋转后的线段A2B2；
（1）作出线段AB关于点P成中心对称的线段A1B1．
22．（10分）计算：
①（﹣a•a2）（﹣b）2+（﹣2a3b2）2÷（﹣2a3b2）
②（x﹣2y）（3x+2y）﹣（x﹣2y）2
23．（10分）已知a、b是实数．
(1)当+(b+5)2=0时，求a、b的值；
(2)当a、b取(1)中的数值时，求(-)÷的值．
24．（10分）如图，∠AFD=∠1，AC∥DE，
(1)试说明：DF∥BC；
(2)若∠1=68°，DF平分∠ADE，求∠B的度数．
25．（12分）如图，△ACB和△ECD都是等边三角形，点A、D、E在同一直线上，连接BE．
(1)求证：AD=BE；
(2)求∠AEB的度数．

26．如图，在平面直角坐标系xOy中，A(-1，5)，B(﹣1，0)，C(﹣4，3)．
（1）在图中画出△ABC关于y轴对称的图形△A1B1C1；（其中A1、B1、C1分别是A、B、C的对应点，不写画法．）
（2）写出点A1、B1、C1的坐标；
（3）求出△A1B1C1的面积．
参考答案
一、选择题（每题4分，共48分）
1、C
【详解】解：∵BE⊥AC，CF⊥AB，
∴∠AEB=∠AFC=∠CED=∠DFB=90°．
在△ABE和△ACF中，
，
∴△ABE≌△ACF（AAS），
∴AE=AF．
∵AC=AB，
∴CE=BF．
在△CDE和△BDF中，
，
∴△CDE≌△BDF（AAS）
∴DE=DF．
∵BE⊥AC于E，CF⊥AB，
∴点D在∠BAC的平分线上．
根据已知条件无法证明AF=FB.
综上可知，①②③正确，④错误，
故选C．
【点睛】
本题考查了全等三角形的判定及性质、角平分线的判定等知识点，要求学生要灵活运用，做题时要由易到难，不重不漏．
2、A
【解析】先证明△ADB≌△EBD，从而可得到AD=DE，然后先求得△AEC的面积，接下来，可得到△CDE的面积．
【详解】解：如图
∵BD平分∠ABC，
∴∠ABD=∠EBD．
∵AE⊥BD，
∴∠ADB=∠EDB．
在△ADB和△EDB中，∠ABD=∠EBD，BD=BD，∠ADB=∠EDB，
∴△ADB≌△EBD，
∴AD=ED．
∵CE=BC，△ABC的面积为2，
∴△AEC的面积为．
又∵AD=ED，
∴△CDE的面积=△AEC的面积=
故选A．
【点睛】
本题主要考查的是全等三角形的判定，掌握等高的两个三角形的面积比等于底边长度之比是解题的关键．
3、B
【分析】根据算术平方根的定义直接求解即可.
【详解】解：4的算术平方根是，
故选B.
【点睛】
本题考查了算术平方根的定义，正确把握定义是解题关键.
4、B
【分析】根据各象限内点的坐标特点，再根据M点的坐标符号，即可得出答案．
【详解】解：∵ 点M（-2019,2019），
∴点M所在的象限是第二象限．
故选B．
【点睛】
本题考查各象限内点的坐标的符号特征，解题的关键是熟记各象限内点的坐标的符号，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．
5、A
【分析】根据全等三角形的判定即可解决问题．
【详解】解：观察图象可知△MNP≌△MFD．
故选：A．
【点睛】
本题考查全等三角形的判定，解题的关键是熟练掌握基本知识，属于中考常考题型．
6、A
【分析】根据欧几里得和《原本》的分析，即可得到答案.
【详解】解：∵《原本》是公理化思想方法的一个雏形。
∴欧几里得首次运用的这种数学思想是公理化思想；
故选：A.
【点睛】
本题考查了公理化思想来源，解题的关键是对公理化思想的认识.
7、A
【分析】利用角平分线的性质可得∠ABD=∠ABC=×70°=35°，再根据三角形外角的性质可得∠BDC=∠A+∠ABD=50°+35°=85°．
【详解】解：∵BD平分∠ABC，∠ABC=70°，
∴∠ABD=∠ABC=×70°=35°，
∵∠A=50°，
∴∠BDC=∠A+∠ABD=50°+35°=85°，
故选A．
【点睛】
此题主要考查了角平分线的定义和三角形外角的性质，关键是掌握三角形的一个外角等于和它不相邻的两个内角的和．
8、A
【分析】由∠BCE=∠ACD可得∠ACB=∠DCE，结合BC=EC根据三角形全等的条件逐一进行分析判断即可．
【详解】∵∠BCE=∠ACD，
∴∠BCE+∠ACE=∠ACD+∠ACE，即∠ACB=∠DCE，
又∵BC=EC，
∴添加AB=DE时，构成SSA，不能使△ABC≌△DEC，故A选项符合题意；
添加∠B=∠E，根据ASA可以证明△ABC≌△DEC，故B选项不符合题意；
添加AC=DC，根据SAS可以证明△ABC≌△DEC，故C选项不符合题意；
添加∠A=∠D，根据AAS可以证明△ABC≌△DEC，故D选项不符合题意，
故选A．
【点睛】
本题考查了三角形全等的判定，准确识图，熟练掌握全等三角形的判定方法是解题的关键．
9、C
【分析】根据众数的定义求解即可.
【详解】∵21出现的次数最多，∴则该地区这10天最高气温的众数是21；故答案选C.
【点睛】
此题考查了众数，解题的关键是正确理解题意，抓住题目中的关键语句.
10、C
【解析】试题分析：如图，根据平行线的性质可得∠1=∠4=75°，然后根据三角形的外角等于不相邻两内角的和，可知∠4=∠2+∠3，因此可求得∠3=75°-35°=40°．
故选C
考点：平行线的性质，三角形的外角性质
11、C
【分析】先进行括号内的计算，然后将除号换为乘号，再进行分式间的约分化简.
【详解】原式=
=
=
=.
故选C.
【点睛】
本题考查分式的混合运算，混合运算顺序为：先乘方，再乘除，然后加减，有括号的先算括号里面的.
12、D
【分析】根据分式有意义的条件是分母不等于零计算．
【详解】由题意得，x−2≠0，
解得，x≠2，
故选：D．
【点睛】
本题考查的是分式有意义的条件，掌握分式有意义的条件是分母不等于零是解题的关键．
二、填空题（每题4分，共24分）
13、（-4，2）或（2，2）
【解析】A、B的纵坐标相同，横坐标为 ，则点B的坐标为（-4，2）或（2，2）
14、50°
【解析】根据全等三角形的对应角相等解答．
【详解】∵两个三角形全等，a与c的夹角是50°，
∴∠α=50°，
故答案是：50°．
【点睛】
考查的是全等三角形的性质，掌握全等三角形的对应角相等是解题的关键．
15、55°
【分析】这道题可以根据CD为斜边AB的中线得出CD=AD，由∠A=35°得出∠A=∠ACD=35°，则∠BCD=90°- 35°=55°.
【详解】如图，∵CD为斜边AB的中线
∴CD=AD
∵∠A=35°
∴∠A=∠ACD=35°
∵∠ACD+∠BCD=90°
则∠BCD=90°- 35°=55°
故填：55°.
【点睛】
此题主要考查三角形内角度求解，解题的关键是熟知直角三角形的性质.
16、如果两个角相等，那么这两个角是同位角．
【解析】因为“同位角相等”的题设是“两个角是同位角”，结论是“这两个角相等”，
所以命题“同位角相等”的逆命题是“相等的两个角是同位角”．
17、9或1．
【详解】把A（a，a），B（b，8b）代入y=kx+m得：
，
解得：k==+1=+1，
∵是整数，k是整数，
∴1﹣=或，
解得：b=2a或b=8a，
则k=1或k=9，
故答案为9或1．
18、＜
【分析】从折线图中得出乙的射击成绩，再利用方差的公式计算，最后进行比较即可解答．
【详解】由图中知，甲的成绩为7，7，8，9，8，9，10，9，9，9，
乙的成绩为8，9，7，10，7，9，10，7，10，8，
甲=（7+7+8+9+8+9+10+9+9+9）÷10=8.5，
乙=（8+9+7+8+10+7+9+10+7+10）÷10=8.5，
甲的方差S甲2=[2×（7-8.5）2+2×（8-8.5）2+（10-8.5）2+5×（9-8.5）2]÷10=0.85，
乙的方差S乙2=[3×（7-8.5）2+2×（8-8.5）2+2×（9-8.5）2+3×（10-8.5）2]÷10=1.35
∴S2甲＜S2乙．
【点睛】
本题考查方差的定义与意义：一般地设n个数据，x1，x2，…xn的平均数为，则方差S2= [（x1-）2+（x2-）2+…+（xn-）2，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．
三、解答题（共78分）
19、 ；
【解析】试题分析:本题考查了分式的化简求值,原式第二项约分后，两项通分并利用同分母分式的加法法则计算得到最简结果，把x=0代入计算即可求出值．
解：原式=+===，
当x=0时，原式=．
20、（1）见解析（2）见解析
【分析】（1）根据题意证明△ABE≌△ADC即可求解；
（2）延长CP至B，使PB=PA，连接AB，证△APB为等边三角形得AP=PB=AB，再证△△BAC≌△PAE得EP=BC，可得.
【详解】（1）
∴
即
又，
∴△ABE≌△ADC
∴
(2)如图，延长CP至B，使PB=PA，连接AB，
∵
∴∠APB=60，又PB=PA，
∴△APB为等边三角形，
∴AP=PB=AB,∠BAP=60，
∵是等边三角形，
∴AC=AE,∠EAC=60∘，
∴∠BAP =∠EAC，
∴∠BAP +∠PAC=∠EAC +∠PAC，
即：∠BAC=∠PAE，
在△BAC和△PAE中，

∴△BAC≌△PAE (SAS)，
∴BC=PE，
∵BC=BP+PC=AP+ PC，
∴.
【点睛】
此题主要考查全等三角形的判定与性质，解题的关键是熟知的等边三角形的性质及全等三角形的判定方法.
21、（1）见解析；（2）见解析；（1）见解析
【分析】（1）根据平移的性质作出A，B的对应点A1，B1，连接即可；
（2）根据旋转的性质作出A，B的对应点A2，B2，连接即可；
（1）根据中心对称的性质作出A，B的对应点A1，B1，连接即可．
【详解】解：（1）如图，线段A1B1即为所求；
（2）如图，线段A2B2即为所求；
（1）如图，线段A1B1即为所求．
【点睛】
本题考查作图−旋转变换，平移变换以及中心对称等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
22、①﹣3a3b2；②2x2﹣8y2
【分析】①先计算乘方运算，在计算乘除运算，最后算加减运算即可得出答案；
②根据多项式乘多项式和完全平方公式可以解答本题．
【详解】①解：（﹣a•a2）（﹣b）2+（﹣2a3b2）2÷（﹣2a3b2）
=﹣a3•b2+4a6b4÷（﹣2a3b2）
=﹣a3b2﹣2 a3b2
=﹣3a3b2
②解：（x﹣2y）（3x+2y）﹣（x﹣2y）2
=3x2+2xy﹣6xy﹣4y2﹣x2+4xy ﹣4y2
=2x2﹣8y2
【点睛】
本题考查整式的混合运算，有乘方、乘除、加减的混合运算中，要按照先乘方后乘除、最后加减的顺序运算，其运算顺序和有理数的混合运算顺序相似．掌握整式的混合运算顺序是解题的关键．
23、 (1)a=2，b=-5；(2)ab， -1．
【解析】（1）根据非负数的性质，可以求得a、b的值；
（2）根据分式的减法和除法可以化简题目中的式子，然后将a、b的值代入化简后的式子即可解答本题．
【详解】(1)∵+(b+5)2=0，
∴a-2=0，b+5=0，
解得，a=2，b=-5；
(2)(-)÷
=
=
=ab，
当a=2，b=-5时，原式=2×(-5)=-1．
【点睛】
本题考查分式的化简求值、非负数的性质，解答本题的关键是明确分式化简求值的方法．
24、（1）证明见解析；（2）68°.
【解析】试题分析：（1）由AC∥DE得∠1=∠C，而∠AFD=∠1，故∠AFD=∠C，故可得证；
（2）由（1）得∠EDF=68°，又DF平分∠ADE，所以∠EDA=68°，结合DF∥BC即可求出结果．
试题解析：（1）∵AC∥DE，
∴∠1=∠C，
∵∠AFD=∠1，
∴∠AFD=∠C，
∴DF∥BC；
（2）∵DF∥BC，
∴∠EDF=∠1=68°，
∵DF平分∠ADE，
∴∠EDA=∠EDF=68°，
∵∠ADE=∠1+∠B
∴∠B=∠ADE-∠1=68°+68°-68°=68°.
25、（1）证明见解析；（2）∠AEB=60°．
【解析】（1）根据等边三角形的性质得出AC=BC，CD=CE，∠ACB=∠DCE=60°，求出∠ACD=∠BCE，然后根据SAS证明△ACD≌△BCE，即可得出AD=BE；
（2）由△ECD是等边三角形可得∠CDE=∠CED=60°，根据补角的性质可求∠ADC=120°，根据全等三角形的性质可得∠BEC=∠ADC=120°，进而根据∠AEB=∠BEC﹣∠CED可得出答案．
证明：（1）∵△ACB和△ECD都是等边三角形，
∴AC=BC，CD=CE，∠ACB=∠DCE=60°，
又∵∠ACD=∠ACB﹣∠DCB，∠BCE=∠DCE﹣∠DCB，
∴∠ACD=∠BCE，
在△ACD和△BCE中，
∴△ACD≌△BCE（SAS）．
∴AD=BE；
（2）在等边△ECD中，
∠CDE=∠CED=60°，
∴∠ADC=120°，
∵△ACD≌△BCE，
∴∠BEC=∠ADC=120°，
∴∠AEB=∠BEC﹣∠CED=120°﹣60°=60°．
点睛：本题考查了等边三角形的性质，全等三角形的判定和性质的应用，能推出△ACD≌△BCE是解此题的关键．
26、（1）见解析；（2）A1(1，5)，B1(1，0)，C1(4，3)；（3）
【分析】（1）根据网格结构找出点A、B、C的对应点A1、B1、C1的位置，然后顺次连接即可；
（2）根据平面直角坐标系写出点的坐标即可；
（3）利用三角形的面积公式列式进行计算即可求解．
【详解】解：（1）如图所示，△A1B1C1即为所求作的三角形；
（2）点A1、B1、C1的坐标分别为：
A1（1，5），B1（1，0），C1（4，3）；
（3）S＝×5×3＝．
【点睛】
本题考查了利用轴对称变换作图，熟悉网格结构并找出对应点的位置是解题的关键．
最高气温(°C)
18
19
20
21
22
天数
1
2
2
3
2