



初中数学北师大版(2024)七年级上册(2024)3 一元一次方程的应用教案配套ppt课件
展开1. 能根据几何图形问题中的数量关系列出方程,感悟数学模型的思想.2.通过对几何图形问题的解决,体会利用方程解决问题的关键是寻找等量关系.3.经历运用方程解决几何图形问题的过程,感受数学与实际的联系,加强应用意识.
寻找几何图形问题中的等量关系,建立方程.
抓住几何图形变化中的不变量,确定等量关系.
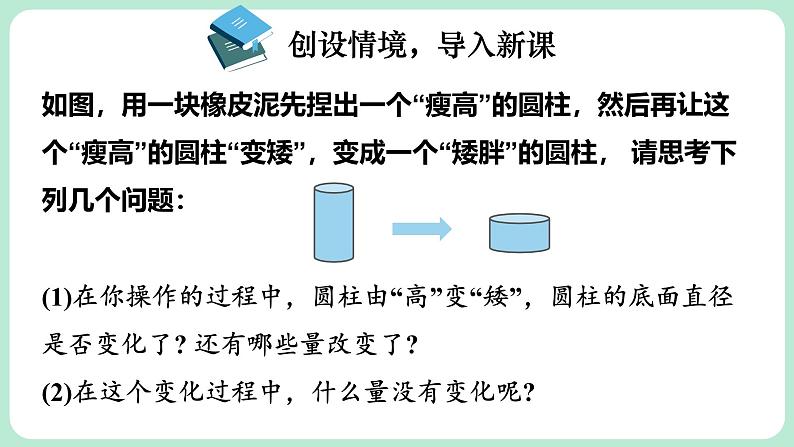
如图,用一块橡皮泥先捏出一个“瘦高”的圆柱,然后再让这个“瘦高”的圆柱“变矮”,变成一个“矮胖”的圆柱, 请思考下列几个问题:
(1)在你操作的过程中,圆柱由“高”变“矮”,圆柱的底面直径是否变化了? 还有哪些量改变了?(2)在这个变化过程中,什么量没有变化呢?
探究点 利用一元一次方程解决几何图形问题
某饮料公司有一种底面直径和高分别为6.6cm,12cm 的圆柱形易拉罐饮料. 经市场调研决定对该产品外包装进行改造,计划将它的底面直径减少为6cm.那么在容积不变的前提下,易拉罐的高度将变为多少厘米?
(1)这个问题中包含哪些量? 它们之间有怎样的等量关系?
包含的量:圆柱形易拉罐改造前后的底面半径、 高、容积
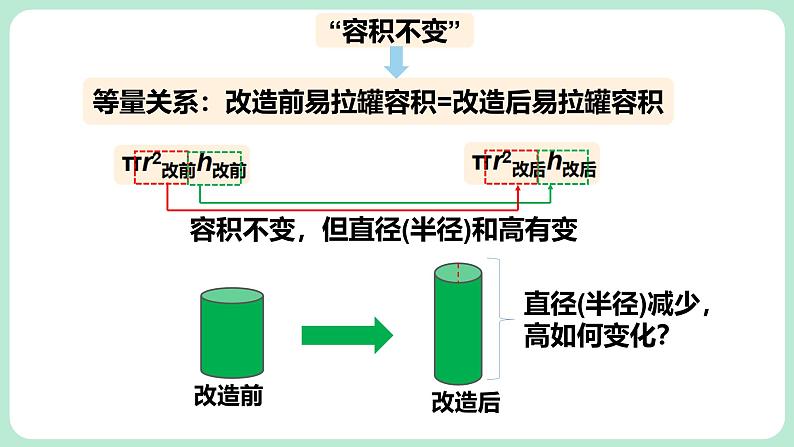
等量关系:改造前易拉罐容积=改造后易拉罐容积
容积不变,但直径(半径)和高有变
直径(半径)减少,高如何变化?
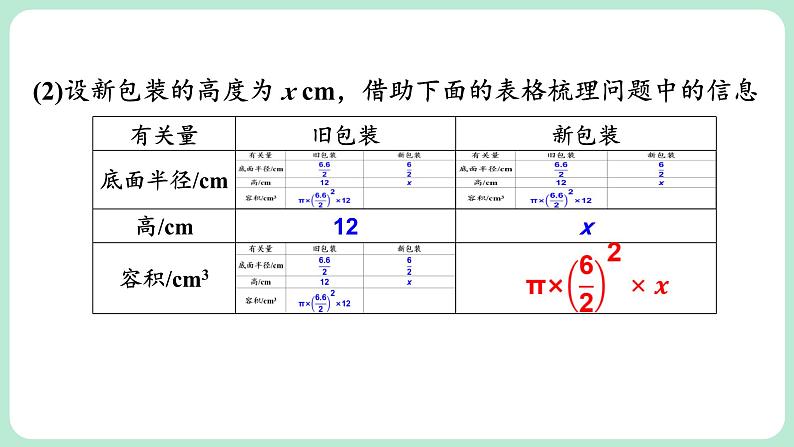
(2)设新包装的高度为 x cm,借助下面的表格梳理问题中的信息
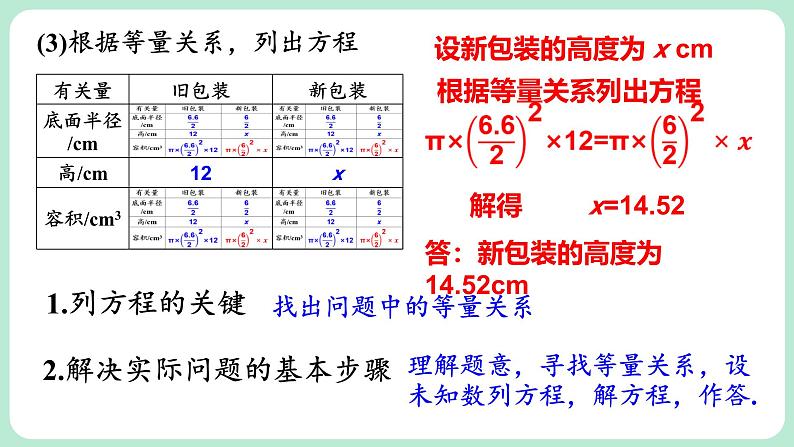
(3)根据等量关系,列出方程
设新包装的高度为 x cm
解得 x=14.52
答:新包装的高度为14.52cm
2.解决实际问题的基本步骤
理解题意,寻找等量关系,设未知数列方程,解方程,作答.
用一根长为10m 的铁丝围成一个长方形.(1)如果该长方形的长比宽多1.4m,那么此时长方形的长、宽各为多少米?(2)如果该长方形的长比宽多0.8m,那么此时长方形的长、宽各为多少米? 此时的长方形与(1)中的长方形相比,面积有什么变化?(3)如果该长方形的长与宽相等,即围成一个正方形,那么此时正方形的边长是多少米? 正方形的面积与(2)中长方形的面积相比又有什么变化?
②如图,题中围长方形的过程中有什么没有发生变化?
长方形的周长(或长与宽的和)不变
铁丝的长,长方形的长、宽、周长、面积.
④如图,结合(1)(2)问题意,若设长方形的宽为 x m,则长方形的长可怎么表示? 试用含 x 的代数式在下面图中表示出来.
③题中有怎样的等量关系?
等量关系: (长+宽)×2=周长(周长就是铁丝的长度)
解:(1)设此时长方形的宽为x m,则它的长为(x+1.4) m.根据题意,得2(x+1.4) +2x=10解得 x=1.8 1.8+1.4=3.2此时长方形的长为3.2m,宽为1.8m.
(1)如果该长方形的长比宽多1.4m,那么此时长方形的长、宽各为多少米?
解:设此时长方形的宽为x m,则它的长为(x+0.8)m. 根据题意,得 2(x+0.8)+2x=10 解得:x=2.1,2.1+0.8=2.9此时长方形的长为2.9m,宽为2.1m, 长方形面积为2.9×2.1=6.09(m2)(1)中长方形的面积为3.2×1.8=5.76(m2),6.09-5.76=0.33(m2)
此时(2)中长方形的面积比(1)中长方形的面积增大0.33m2
(2)如果该长方形的长比宽多0.8m,那么此时长方形的长、宽各为多少米? 此时的长方形与(1)中的长方形相比,面积有什么变化?
(3)设正方形的边长为x m根据题意,得 4x=10 解得 x=2.5正方形的边长为 2.5m,面积为 2.5×2.5=6.25(m2),比(2)中长方形的面积增大 6.25-6.09=0.16(m2)
(3)如果该长方形的长与宽相等,即围成一个正方形,那么此时正方形的边长是多少米? 正方形的面积与(2)中长方形的面积相比又有什么变化?
所列方程的两边分别表示 长方形的周长和铁丝的长度列方程的思路 先设一边长为未知数,再用含未知数的代数式表示出周长,根据周长等于铁丝的长度10m这个等量关系列出方程.
在前面的问题中,所列方程的两边分别表示什么量?列方程的思路是什么?
总结:周长一定的长方形,长和宽的差值越小,长方形的面积越大;当长和宽相等时(即为正方形时),长方形(正方形)的面积最大.
一个梯形的下底比上底多6cm,高是8cm,面积为88cm2,求这个梯形的上底和下底的长度.
解:设梯形的上底为x cm,则下底为(x+6)cm
答:梯形的上底为8cm,下底为14cm.
【选自教材P149 随堂练习】
1.直径为30cm、高为50cm 的圆柱形瓶里装满了饮料,现将饮料倒入底面直径为10cm 的圆柱形水杯,刚好倒满30杯,则水杯的高度是多少?
解:设水杯的高度为x cm
解得 x=15
答:水杯的高度为15cm
一个长方形的周长是40cm,若将长减少6cm,宽增加2cm,长方形就变成了正方形,则长方形的长、宽各为多少厘米?
解得 x=14
答:长方形的长为14cm,则宽为6cm.
*利用一元一次方程解决一般几何图形问题
(1)有一块边长为4cm 的正方体形橡皮泥,要用它来捏一个长、宽分别为8cm,2cm 的长方体橡皮泥,求它的高.
(2)如图,小明将一张正方形纸片剪去一个宽为6cm 的长条后,再从剩下的长方形纸片上剪去一个宽为8cm 的长条,如果两次剪下的长条面积正好相等,那么每一个长条的面积为多少?
解:设正方形的边长为 x cm
答:每一个长条的面积为144cm2
(3)用一根120cm 长的铁丝围成一个长方形,使该长方形的长是宽的2倍,则这个长方形的长、宽分别为多少?
解:设长方形的宽为x cm,则长为2x cm.
2(x+2x)=120
答:长方形的宽为20cm,长为40cm
*培优点 利用一元一次方程解决拼接图形问题
如图,周长为68的长方形ABCD 被分成7个相同的小长方形,则长方形ABCD 的面积为多少?
答:长方形ABCD 的面积为280.
1.两个圆柱体容器如图所示,它们的底面直径分别为4 cm和8 cm,高分别为39 cm和 10 cm. 先在右侧容器中倒满水,然后将其倒入左侧容器中. 倒完以后,左侧容器中的水面离容器口有多少厘米?小刚是这样做的:设倒完以后,左侧容器中的水面离容器口有x cm. 列方程 π×22×(39-x)= π×42×10. 解得x=-1. 请你对他的结果作出合理的解释.
【选自教材P154 习题5.3 第1题】
解:由题意可知,第一个容器的体积为22×39×π = 156π cm2第二个容器的体积为42×10×π = 160π cm2 第二个容器的体积大于第一个容器的体积,因此将第二个容器装满水后再倒入第一个容器中,水会溢出,即方程 π×22×(39-x)= π × 42×10的解小于0.
2.现有两块试验田,第一块试验田的面积比第二块试验田面积的3倍还多100 m2,这两块试验田的面积共2900 m2,两块试验田的面积分别是多少?
解:设第二块试验田的面积是 x m2,则第一块试验田的面积是(3x + 100)m2 根据题意,得 x + 3x + 100 = 2900 解得 x = 700 所以 3x + 100 = 2200答:第一块试验田的面积是 2200 m2,第二块试验田的面积是 700 m2
【选自教材P154 习题5.3 第3题】
3.如图,小强将一个正方形纸片剪去一个宽为4 cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm 的长条. 如果两次剪下的长条面积正好相等,那么每一个长条的面积为多少?
解:设正方形的边长为 x cm根据题意,得 4x = 5(x - 4)解得 x = 20所以每一个长条的面积为 4×20 = 80(cm2)答:每一个长条的面积为 80 cm2.
【选自教材P154 习题5.3 第4题】
4.如图,某种卷筒纸的外直径为14 cm,内直径为6 cm,每层纸的厚度为0.02 cm. 假如把这筒纸全部拉开,那么这筒纸的总长度大约是多少米(π取3.14)?
【选自教材P154 习题5.3 第5题】
解:设卷筒纸的宽度为 x cm
卷筒纸的总长度为:40πx÷0.02x≈6280(cm)=62.8(m)
答:卷筒纸的总长度为62.8m
初中数学北师大版(2024)七年级上册(2024)3 一元一次方程的应用课前预习ppt课件: 这是一份初中数学北师大版(2024)七年级上册(2024)<a href="/sx/tb_c4050010_t3/?tag_id=26" target="_blank">3 一元一次方程的应用课前预习ppt课件</a>,共18页。PPT课件主要包含了68π,长×宽×高,底面积×高,×长+宽,长×宽,针对练习等内容,欢迎下载使用。
初中沪科版(2024)3.3 一元一次方程的应用课前预习ppt课件: 这是一份初中沪科版(2024)<a href="/sx/tb_c4053958_t3/?tag_id=26" target="_blank">3.3 一元一次方程的应用课前预习ppt课件</a>,共18页。PPT课件主要包含了复习回顾,探索新知,解方程得x20,形积变化中的等量关系,练一练,注意单位换算,解方程得x6,实际问题,归纳总结,随堂练习等内容,欢迎下载使用。
初中北师大版(2024)3 一元一次方程的应用课文配套ppt课件: 这是一份初中北师大版(2024)<a href="/sx/tb_c4050010_t3/?tag_id=26" target="_blank">3 一元一次方程的应用课文配套ppt课件</a>,共31页。PPT课件主要包含了学习目标,素养目标,学习难点,学习重点,追及问题,小明先出发的路程,爸爸追小明的路程,根据题意得,x400,化简得等内容,欢迎下载使用。













