数学七年级上册（2024）3.1 方程课堂教学ppt课件

这是一份数学七年级上册（2024）3.1 方程课堂教学ppt课件，文件包含第2课时等式的基本性质pptx、等式的性质mp4等2份课件配套教学资源，其中PPT共19页， 欢迎下载使用。

判断：下列各式中哪些是等式？
用等号表示相等关系的式子叫作等式.
通常用a=b表示一般的等式.
对于方程x+2=4，3x=6，你能用所学知识求出它们的解吗?
方程是等式，解方程的过程实际上就是等式的变形过程. 为了进一步讨论解方程，我们先来看看等式有什么性质.
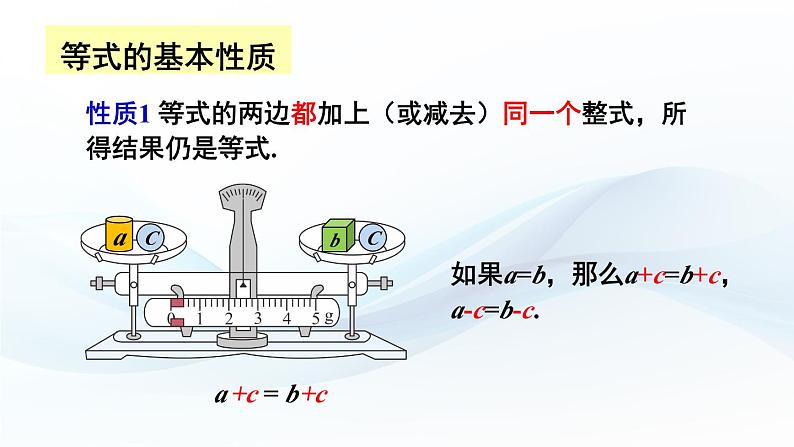
观察：如图，在一台天平两端的托盘中分别放置了质量为a，b的物体，天平平衡，这直观地说明 a = b.
同时加上质量为c的物体，天平还保持平衡吗?
性质1 等式的两边都加上（或减去）同一个整式，所得结果仍是等式.
如果a=b，那么a+c=b+c，a-c=b-c.
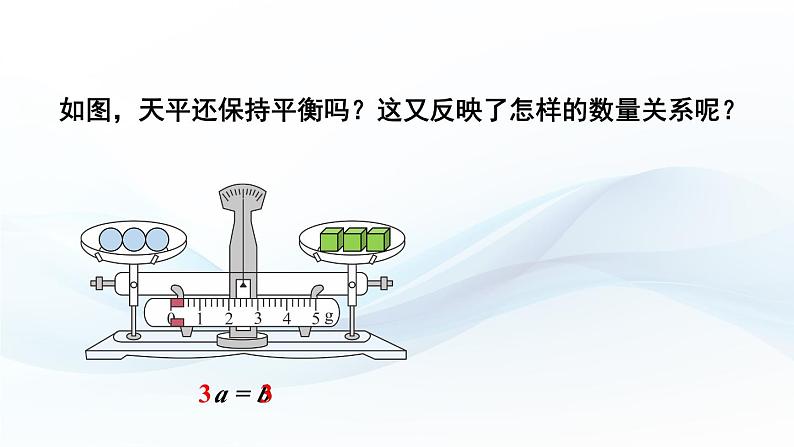
如图，天平还保持平衡吗？这又反映了怎样的数量关系呢？
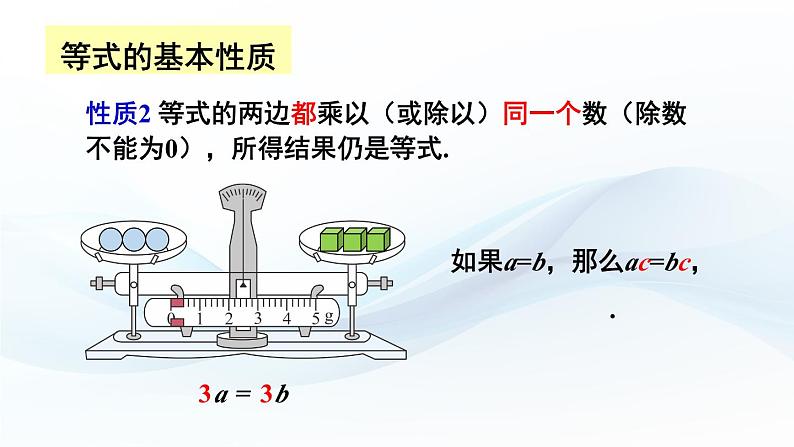
性质2 等式的两边都乘以（或除以）同一个数（除数不能为0），所得结果仍是等式.
如果a=b，那么ac=bc， .
性质3（对称性） 如果a=b，那么b=a.
性质4（传递性） 如果a=b，b=c，那么a=c.
根据等式这一性质，将一个量用与它相等的量代替，称为等量代换.
指出下列等式变形的依据.（1）如果5x+3=7，那么5x=4；（2）如果﹣8x=4，那么x= ；（3）如果﹣5a=﹣5b，那么a=b；（4）如果3x=2x+1，那么x=1；（5）如果﹣0.25=x，那么x=﹣0.25；（6）如果x=y，y=z，那么x=z.
【教材P96 练习 第1题】
例2：解方程：3x - 3 = 21.
解：两边都加上3，得 3x = 21+3，（性质1）
两边同除以3，得 x = 8.（性质2）
检验：把 x = 8 代入原方程，得
左边=3×8-3=21，
所以x=8是原方程的解.
根据等式的基本性质解方程，并检验：1.8x=2.5x+1.4.
解：两边都减去2.5x，得 -0.7x = 1.4，（性质1）
两边同除以-0.7，得 x = -2.（性质2）
检验：把 x = -2 代入原方程，得左边=1.8×(-2)=-3.6，右边=2.5×(-2)+1.4=-3.6，左边=右边.所以x=-2是原方程的解.
2.下列变形中错误的是（ ）A.若x=y，则x+a=y+aB.若mx=my，则x=yC.若x+a=y+a，则x=yD.若x=y，则mx=my
1.由2x=-4得x=-2，变形的依据是根据等式的（ ）A.基本性质1B.基本性质2C.基本性质3D.基本性质4
3.解方程并检验.（1）5x -7 =8；（2）27=7+4x；（3） .
【教材P96 练习 第2题】
（1）解：两边都加上7，得5x=8+7，（性质1）即5x=15.两边同除以5，得x=3.（性质2）检验：把x=3代入原方程，得左边=5×3-7=8，右边=8，左边=右边. 所以x=3是原方程的解.
（2）解：由对称性，得7+4x=27.（性质3）两边都减去7，得4x=27-7，（性质1）即4x=20.两边同除以4，得x=5.（性质2）检验：把x=5代入原方程，得左边=27，右边=7+4×5=27，左边=右边. 所以x=5是原方程的解.
4.*已知2x2 – x=5，求多项式– 4x2 +2x – 8的值.
解：因为2x2 – x = 5，所以在等式两边都乘以– 2，得–2(2x2 – x)=5×(–2). 化简，得 – 4x2+2x= – 10. 等式两边都减去8，得 – 4x2+2x – 8= – 10 – 8. 所以– 4x2+2x – 8 = – 18.