初中沪科版（2024）3.3 一元一次方程的应用课前预习ppt课件

这是一份初中沪科版（2024）3.3 一元一次方程的应用课前预习ppt课件，共18页。PPT课件主要包含了复习回顾，探索新知，解方程得x20，形积变化中的等量关系，练一练，注意单位换算，解方程得x6，实际问题，归纳总结，随堂练习等内容，欢迎下载使用。

常见几何体的体积、面积公式：
（1）长方体的体积=长×宽×高；
（2）正方体的体积=棱长×棱长×棱长；
（3）圆柱的体积=底面积×高；
（4）长方形的面积=长×宽；
（5）正方形的面积=边长×边长；
（6）梯形的面积= (上底+下底)×高.
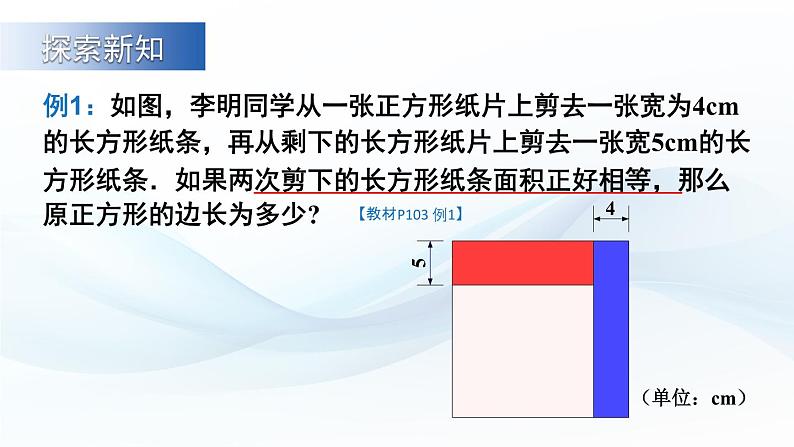
例1：如图，李明同学从一张正方形纸片上剪去一张宽为4cm的长方形纸条，再从剩下的长方形纸片上剪去一张宽5cm的长方形纸条．如果两次剪下的长方形纸条面积正好相等，那么原正方形的边长为多少?
【教材P103 例1】
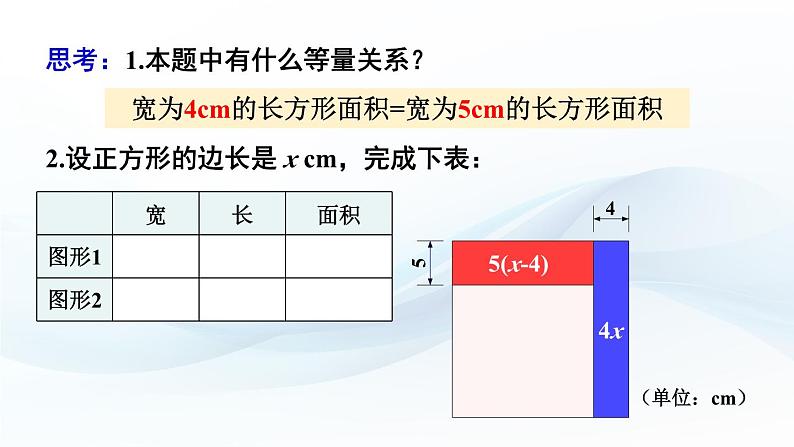
思考：1.本题中有什么等量关系？
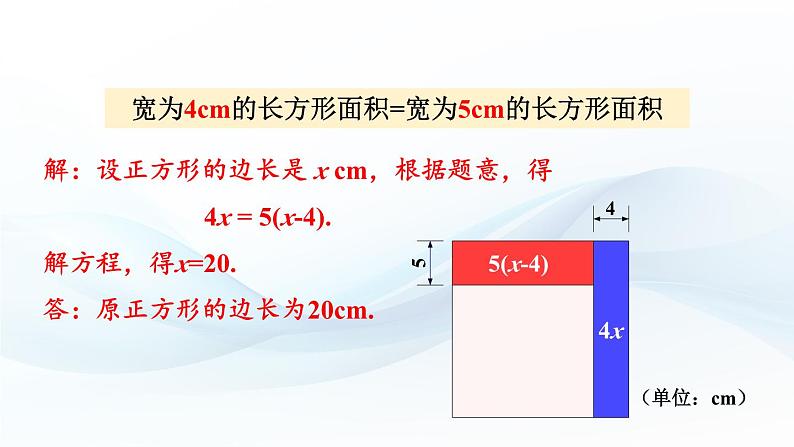
宽为4cm的长方形面积=宽为5cm的长方形面积
2.设正方形的边长是 x cm，完成下表：
解：设正方形的边长是 x cm，根据题意，得
4x = 5(x-4).
答：原正方形的边长为20cm.
①形状发生了变化，体积/面积不变. 其相等关系是：变化前图形的体积/面积=变化后图形的体积/面积
②形状、面积发生了变化，周长不变. 其相等关系是：变化前图形的周长=变化后图形的周长
③形状、体积不同，面积相同．根据题意找出面积之间的关系，即相等关系．
如图，长方形纸片的长是15cm，现从 长、宽上各剪去一个宽为3cm的长条，剩下的面积是原长方形面积的 .求原长方形纸片的宽.
解：设原长方形纸片的宽为x cm，则剩下的长方形的长为15-3=12(cm)，宽为(x-3)cm.
答：原长方形纸片的宽为12cm.
例2：某县举办越野赛. 选手从起点出发，先沿着山区公路跑步到达补给站，再登山到达比赛终点. 张老师参加了这个比赛，他的相关数据如下表：
已知张老师在补给站休息了10min，用时1.5h完成了比赛.求补给站与起点的距离.
跑步距离+登山距离=总距离
【教材P103 例2】
跑步时间+登山时间=总用时-休息时间
解：设补给站离起点x km. 根据题意，得
答：补给站与起点的距离为6km.
交流：运用一元一次方程解决实际问题的基本过程是怎样的？
数学问题（一元一次方程）
数学问题的解（一元一次方程的解）
“读万卷书，行万里路”，经历是最好的学习，研学是最美的相遇. 11月中旬七年级的学生开启了以“溯源千年谯城·浸润万缕药香”为主题的亳州研学之旅. 已知①号车和②号车同时从合肥出发沿同一路线开往亳州，①号车的行驶速度是 80km/h，②号车的行驶速度是72km/h，①号车比②号车早到 h，求合肥与亳州相距多少千米?
解：设合肥与亳州相距x km.
根据题意，得 ，解得x=320.
答：合肥与亳州相距320km.
列方程解应用题的一般步骤如下：
⑴弄清题意和题中的数量关系，用字母（如x，y）表示问题涉及的未知数；
⑵分析题意，找出等量关系（可借助示意图、表格等）；
⑶根据等量关系，列出需要的代数式，并列出方程；
⑷解这个方程，求出未知数的值；
⑸检查所得的值是否正确和符合实际情形，并写出答案（包括单位）.
1.列方程，解下列各题：（1）一种小麦磨成面粉，出粉率为80%（即20%成为麸子）．为了得到4500 kg面粉，至少需要多少小麦?
【教材P104 练习】
解：设至少需要x kg小麦. 根据题意，得x·80％ = 4500.解方程，得x=5625. 答：至少需要 5625 kg小麦.
（2）甲厂有钢材432t，乙厂有钢材96t．如果每天从甲厂运出20t，乙厂运出4t，几天后甲厂剩余的钢材是乙厂的2倍?
解：设x天后，甲厂剩余的钢材是乙厂的2倍. 根据题意，得432-20x=2(96-4x). 解方程，得x=20. 答：20天后，甲厂剩余的钢材是乙厂的2倍.
（3）甲、乙两地相距180km．一人骑自行车从甲地出发，每小时骑行15km．另一人骑摩托车从乙地同时出发．两人相向而行．已知摩托车车速是自行车车速的3倍．多少时间后两人相遇？
解：设x h后两人相遇. 根据题意，得x(15+15×3)=180.解方程，得x=3. 答：3h后两人相遇.
2.有一根合金圆柱，底面半径为1 dm，高为64 cm，若将其锻造成长方体工件，使长方体工件的长为20π cm，高为32 cm，则长方体工件的宽是多少?
解：设长方体工件的宽是x cm.1 dm=10 cm，根据题意，得π×102×64=20π×32x，解得x=10.答：长方体工件的宽是10cm.
3. 甲、乙两人从相距200km的两地相向而行，甲乘汽车每小时行60km，乙骑自行车每小时行20km. 如果乙先行2h，那么甲出发多长时间后两人相遇?
解：设甲出发x h后两人相遇.根据题意，得60x+20(x+2)=200，解得x=2.答：甲出发2h后两人相遇.